Министерство образования и науки Российской Федерации

Казанский национально исследовательский технический университет

им. А.Н. Туполева - КАИ

Институт технической кибернетики и информатики

Кафедра ИТП ЭВС

Пояснительная записка к курсовому проекту по дисциплине

"Микропроцессоры в конструкциях и технологии ЭВС"

Разработка Микропроцессорного генератора треугольных импульсов

Выполнил: студент гр. 4413

Вафин И.Р._____________

Научный руководитель:

доцент кафедры ИТП ЭВС

Невзоров В. Н. ______________

Оценка:___________

«____» ______________2012 г.

Казань 2012

Содержание

Задание по курсовому проекту 3

1.Математическая модель 4

2.Концептуальный алгоритм 9

3.Структурная схема 12

4.Описание принципиальной схемы 15

5.Особенности программного обеспечения 17

Список литературы 19

Приложение 1. Листинг программы 22

Приложение 2. Перечень элементов 29

Министерство образования и науки РФ

Казанский национальный исследовательский технический университет им. А.Н.Туполева

­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­Кафедра Информационных технологий проектирования ЭВС

Задание

на курсовой проект по дисциплине МП КИТ ЭВС

Студент Вафин И.Р. Группа 4413

Руководитель Невзоров В.Н.

Дата выдачи задания   Срок защиты проекта ­­­­­­­­­­­­­­­­­­­­­­­­­­­­ .12.2012

Тема проекта

Разработать микропроцессорный генератор треугольных импульсов с задаваемой длительностью переднего фронта

со следующими рабочими параметрами:

Частота следования импульсов, Гц 100

Амплитуда выходного сигнала, В 1

Длительность переднего фронта, % 0 – 100 Точность реализации значений параметров, % 5

используя следующую элементную базу для реализации блоков МПС:

генератор тактовых импульсов	К176
блок сопряжения МП с магистралью	K589
порты	К531
постоянное запоминающее устройство	К558
оперативное запоминающее устройство	К565динам
цифрово-аналоговый преобразователь	К572

_________________ Руководитель задания Невзоров В.Н

(подпись)

1. Математическая модель

Микропроцессорный генератор треугольных импульсов позволяет генерировать треугольный импульсный сигнал с частотой следования 100 Гц, амплитудой равной 1В и с длительностью переднего фронта задаваемую пользователем в процентах от 0 до 100.

Под математической моделью будем называть модель-формулу (систему формул), которая позволяет микропроцессору вычислить выходные параметры задачи для последующей их реализации с помощью исполнительных устройств и предъявление результата пользователю системы.

На рис. 1 показана модель процесса, который протекает в данной микропроцессорной системе. Процессор является числовым исполнителем, то есть реализует требуемый процесс дискретно (скачками).

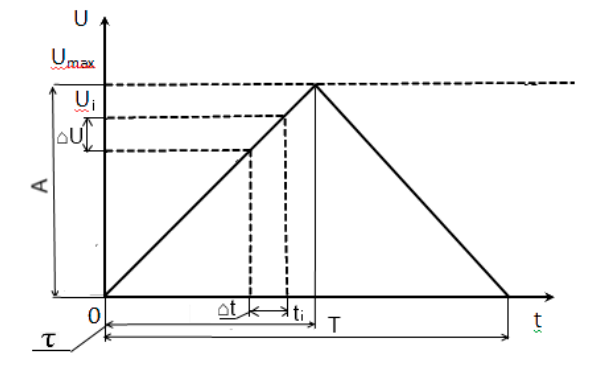
Рис.1

где U – напряжение;

t – время;

U_max – амплитуда выходного напряжения;

Т – период;

– данный момент времени.

- длина переднего фронта волны;

шаг дискретизации по времени;

T – период;

Ui – моментальное напряжение

A – амплитуда;

По оси ОY измеряется напряжение импульса U, по оси ОХ - время t. С учетом дискретизации процесса сигнал выглядит скачкообразным, то есть полный период импульса делится на элементарные временные интервалы Δt. Поэтому для реализуемой точности δ требуется решить вопрос дискретизации.

Так как период и частота обратно пропорциональны, выразим период Т через частоту следования импульса f :

Т = .

Так как процессор реализует требуемый процесс дискретно, что приводит к искажению формы реализуемого (или контролируемого) процесса. Поэтому необходимо для обеспечения заданной точности  проработать вопрос о дискретизации процесса по времени и по рассчитываемому параметру U.

На основе теоремы Котельникова частота дискретизации процесса должна быть не менее 2 х , где – максимальная частота рассматриваемого процесса. Обычно для практических приложений следует выбирать

= 4…5 х ,

Расчет элементарного временного интервала t:

t ≤  / (2 х ), тогда t ≤ 0,05/ 2 x 100 = 0,00025c.

Математически опишем треугольную функцию:

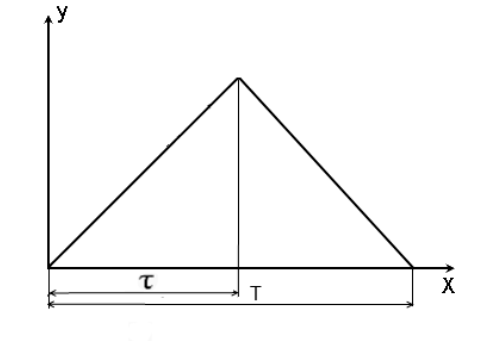
Рис.2

Теперь запишем периодическую треугольную функцию.

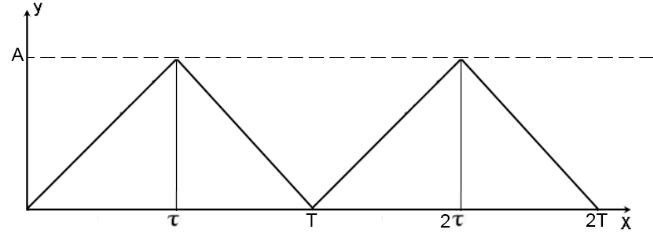
Рис.3

j – количество периодов;

Теперь используем полученную формулу для математического описания генератора треугольных импульсов.

Где A – амплитуда;

T – период;

τ – длинна переднего фронта.

Так как мы описали генератор треугольных импульсов с задаваемым передним фронтом,

Теперь зададим периодичность:

Теперь преобразуем формулу, используя дискретное представление времени, обозначим один такт как n.

Tn=T/t

Tn=0,01/0,00025=40

Tn*k/100

Это и есть искомая математическая модель.