4. Функция Эйлера

Функция Эйлера  , где   — натуральное число, равна количеству натуральных чисел, не больших  и взаимно простых с ним.

Свойства

• , если   — простое число

• Функция Эйлера мультипликативна, т. е.       ,  если   и   взаимно просты.

• (Теорема Эйлера) 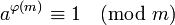      ,  если   и   взаимно просты.

Вычисление функции Эйлера

Пусть дано натуральное число  , представленное в виде его канонического разложения на простые сомножители 

Тогда функция Эйлера может быть вычислена по формуле

При этом полагается, что

Функцию Эйлера можно также представить в виде так называемого произведения Эйлера:

где   — простое число и пробегает все значения, участвующие в разложении   на простые сомножители.

Также иногда функцией Эйлера называют функцию от рационального числа  :

Свойства

1. , если   — простое число. В частности, при 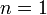  имеем  ;

2. , если   и   взаимно просты. То есть Функция Эйлера мультипликативна;

3. , если   и   взаимно просты. Так называемая теорема Эйлера;

4. 

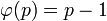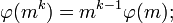
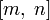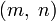5. , если   — наименьшее общее кратное, a   — наибольший общий делитель.

5. Битовые операции

Битовая операция в программировании — некоторые операции над цепочками битов. В программировании, как правило, рассматриваются лишь некоторые виды этих операций: логические побитовые операции и битовые сдвиги. Битовые операции применяются в языках программирования и цифровой технике, изучаются в дискретной математике.

Побитовое отрицание (not)

Побитовое отрицание (или побитовое НЕ, или дополнение) — это унарная операция, действие которой эквивалентно применению логического отрицания к каждому биту двоичного представления операнда. Другими словами, на той позиции, где в двоичном представлении операнда был 0, в результате будет 1, и, наоборот, где была 1, там будет 0. Например:

НЕ	01
	10

Побитовое и (and)

Побитовое И — это бинарная операция, действие которой эквивалентно применению логического И к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, если оба соответствующих бита операндов равны 1, результирующий двоичный разряд равен 1; если же хотя бы один бит из пары равен 0, результирующий двоичный разряд равен 0.

Пример:

И	0011
	0101
	0001

Побитовое или (or)

Побитовое ИЛИ — это бинарная операция, действие которой эквивалентно применению логического ИЛИ к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, если оба соответствующих бита операндов равны 0, двоичный разряд результата равен 0; если же хотя бы один бит из пары равен 1, двоичный разряд результата равен 1.

Пример:

ИЛИ	0011
	0101
	0111

Битовый сдвиг

К битовым операциям также относят битовые сдвиги. При сдвиге значения битов копируются в соседние по направлению сдвига. Различают несколько видов сдвигов — логический,арифметический и циклический, в зависимости от обработки крайних битов.

Также различают сдвиг влево (в направлении от младшего бита к старшему) и вправо (в направлении от старшего бита к младшему).