Якщо та , то

,

,

.

Тобто порівняння за тим самим модулем можна почленно складати, віднімати та множити.

3. Якщо і , то

,

.

Властивості порівнянь, що залежать від модуля m

4. Якщо і , то

або .

5. Обидві частини порівняння можна розділити на їх спільний дільник d, якщо НСД (d, m)=1.

6. Якщо , то , де .

7. Якщо і НСД(k, m)=d, то

.

8. Якщо , то НСД(a,m)=НСД(b,m).

1.7 Теореми Ферма та Ейлера

Теореми Ферма та Ейлера відіграють важливу роль в асиметричних криптографічних системах.

Теорема Ферма

Якщо p – просте число, і a є додатним цілим числом, що не ділиться на p, то

. (1.5)

Доведення. Відомо, що якщо всі елементи множини помножити на а за модулем р, то в результаті отримаємо всі елементи в деякій перестановці. Крім того, . Тому набір (р–1) чисел являє собою той самий набір чисел {1,2, …, (p–1)} в іншому порядку. Перемножимо всі ці числа:

З іншого боку

.

Тому

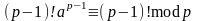(1.6)

Числа (p-1) і p – взаємно прості, тому рівність (1.6) можна скоротити на . Звідси . Теорема доведена.

Теорема Ейлера

Для будь-яких взаємно простих чисел a та m (mN, m>1)

(1.7)

Доведення. Рівність (1.7) справедлива, якщо m є простим числом, тому що в такому випадку і виконується теорема Ферма. Однак та сама рівність виконується і для будь-якого цілого числа m взагалі. Нагадаємо, що дорівнює числу додатних цілих значень, менших m і взаємно простих з m. Розглянемо множину таких цілих чисел, пронумерувавши їх у такий спосіб

.

Тепер помножимо кожен елемент множини L на а за модулем m

.

Наведена множина представляє перестановку елементів множини L з таких причин:

по-перше, оскільки а, як і , є взаємно простим з m, теж повинно бути взаємно простим з m. Таким чином, всі елементи є цілими числами, меншими m і взаємно простими з m;

по-друге, у множині немає повторень. Відповідно до властивостей порівнянь, якщо , то . Тому

,

.

Теорема доведена.

Шифри перестановки

3.1.1 Шифр перестановки “Сциталла”

У V столітті до нашої ери правителі Спарти мали добре відпрацьовану систему секретного військового зв’язку і шифрували свої послання за допомогою сциталла, першого найпростішого криптографічного пристрою, що реалізує метод простої перестановки.

Шифрування виконувалося в такий спосіб. На стрижень циліндричної форми, що називався сциталла, намотували спіраллю (виток до витка) смужку пергаменту й писали на ній уздовж стрижня кілька рядків тексту повідомлення (рис. 3.1). Потім знімали зі стрижня смужку пергаменту з написаним текстом. Букви на цій смужці виявлялися розташованими хаотично. Такий самий результат можна одержати, якщо букви повідомлення писати по кільцю не підряд, а через певне число позицій доти, поки не буде вичерпаний весь текст.

Рисунок 3.1 – Шифр “Сциталла”

Повідомлення «НЕДОПУСТИМІ ЗНАЧЕННЯ» при розміщенні його по окружності стрижня по п’ять букв дає шифротекст

НУІЧЕ С_ЕДТ ЗНОИН НПМАЯ.

Для розшифрування такого шифротексту потрібно не тільки знати правило шифрування, але й мати ключ у вигляді стрижня певного діаметра. Знаючи тільки вид шифру, але, не маючи ключа, розшифрувати повідомлення було непросто. Шифр “Сциталла” багаторазово вдосконалювався в наступні часи.

3.1.2 Таблиці для шифрування

У розроблених шифрах перестановки епохи Відродження (кінець XIV сторіччя) застосовуються таблиці, що шифрують, які, по суті, задають правила перестановки букв у повідомленні.

У ролі ключа таблиці для шифрування використовують:

• розмір таблиці;

• слово або фразу, що задають перестановку;

• особливості структури таблиці.

Таблиці для шифрування. Проста перестановка

Одним із самих примітивних табличних шифрів перестановки є проста перестановка, для якої ключем є розмір таблиці. Цей метод шифрування подібний із шифром сциталла.

Наприклад, повідомлення «ЗАГРОЗА ІСНУЄ ЗАВЖИ І ВСЮДИ» записується в таблицю по стовпцях. Результат заповнення таблиці з 4 рядків і 6 стовпців показаний на рис. 3.2.

Рисунок 3.2 – Заповнення таблиці з 4 рядків і 6 стовпців

Після заповнення таблиці текстом повідомлення по стовпцях для формування шифротексту зчитують вміст таблиці по рядках.

Якщо шифротекст записувати групами по чотири букви, виходить таке шифроване повідомлення:

ЗАЗІ АІАВ ГСВС РНЖЮ ОУДД ЗЄИИ

Природно, відправник і одержувач повідомлення повинні заздалегідь домовитися про загальний ключ – розмір таблиці.

Таблиці для шифрування. Одиночна перестановка по ключу

Трохи більшою стійкістю до розкриття володіє метод шифрування, який називають одиночною перестановкою по ключу. Цей метод відрізняється від попередніх тим, що стовпці таблиці переставляються за ключовим словом, фразою або набором чисел. Довжина ключового слова задає кількість стовпців таблиці.

Візьмемо як ключ, наприклад, слово “ЗАХИСТ”, а текст повідомлення візьмемо з попереднього прикладу. На рис. 3.3 показані дві таблиці, заповнені текстом повідомлення та ключовим словом при цьому ліва таблиця відповідає заповненню до перестановки, а права таблиця – заповненню після перестановки.

Рисунок 3.3 – Таблиці, заповнені ключовим словом і текстом повідомлення

У верхньому рядку лівої таблиці записаний ключ, а номери під буквами ключа визначені відповідно до природного порядку відповідних букв ключа в алфавіті. Якби в ключі трапилися однакові букви, вони б були понумеровані зліва на право. У правій таблиці стовпці переставлені відповідно до порядкових номерів букв ключа.

При зчитуванні вмісту правої таблиці по стовпцях і запису шифротексту групами по п’ять букв одержимо шифроване повідомлення:

АІАВЗ АЗІРН ЖЮОУД ДЗЄИИ ГСВС

Таблиці для шифрування. Подвійна перестановка

Для забезпечення додаткової секретності можна повторно зашифрувати повідомлення, що вже пройшло шифрування. Такий метод шифрування називається подвійною перестановкою. У випадку подвійної перестановки стовпців і рядків таблиці перестановки визначаються окремо для стовпців і окремо для рядків. Спочатку в таблицю записується текст повідомлення, а потім по черзі переставляються стовпці, а потім рядки. При розшифруванні порядок перестановок повинен бути зворотним.

Наприклад, виконаємо методом подвійної перестановки шифрування тексту «ЗАГРОЗА ІСНУЄ ЗАВЖИ І ВСЮДИ» із ключем 416325 (стовпці) 2431 (рядки).

Шифрування тексту методом подвійної перестановки показано на рис. 3.4.

Якщо зчитувати шифротекст із правої таблиці порядково блоками по п’ять літер, то вийде таке:

ВДЮІИ САОРЗ ЗГАДЖ ЗИВІУ НАЄС.

Рисунок 3.4 – Приклад виконання шифрування методом подвійної перестановки

Число варіантів подвійної перестановки швидко зростає при збільшенні розміру таблиці.

Однак подвійна перестановка не відрізняється високою стійкістю та порівняно просто «зламується» при будь-якому розмірі таблиці шифрування.

Застосування магічних квадратів

Магічними квадратами називають квадратні таблиці, в кожну клітинку яких вписано послідовні натуральні числа починаючи з 1, які дають у сумі по кожному стовпцю, кожному рядку і кожній діагоналі те саме число.

Текст, що шифрується, вписується в магічні квадрати відповідно до нумерації їх клітинок. Якщо потім виписати вміст такої таблиці по рядках, то вийде шифротекст, сформований завдяки перестановці букв вихідного повідомлення.

Наприклад, методом магічного квадрата виконати шифрування тексту «ВІРТУАЛЬНИЙ КАНАЛ» .

Шифрування тексту зробимо з використанням магічного квадрата розміром 44 (рис. 3.5) .

Рисунок 3.5 – Приклад магічного квадрата 44

і його заповнення повідомленням

Шифротекст, який одержали при зчитуванні вмісту правої таблиці по рядках групами по чотири букви, має такий вигляд:

ЛРІА УИЙЬ НАЛК ТАНВ.

Число магічних квадратів швидко зростає зі збільшенням розміру квадрата. Існує тільки один магічний квадрат розміром 33 (якщо не враховувати його повороти). Кількість магічних квадратів 44 становить уже 880, а кількість магічних квадратів 55 – близько 250000.

3.2 Шифри простої заміни

При шифруванні заміною (підстановкою) символи тексту, що шифруються, замінюються символами того самого або іншого алфавіту із заздалегідь установленим правилом заміни. У шифрі простої заміни кожен символ вихідного тексту замінюється символами того самого алфавіту однаково протягом всього тексту. Часто шифри простої заміни називають шифрами одноалфавітної підстановки.

Математичний аналіз шифру простої заміни (підстановки)

Нехай маємо деякий алфавіт , який можна подати так:

.

Поєднуючи за певним правилом букви алфавіту , можна створити нові алфавіти:

алфавіт , що містить біграм

;

алфавіт , що містить 3-грам

.

У загальному випадку, поєднуючи по n букв, одержуємо алфавіт , що містить n-грам.

Встановимо взаємно однозначну відповідність між алфавітом  і множиною цілих чисел

.

Надалі будемо використовувати алфавіт , що містить m «букв» (у вигляді чисел).

Текст, який містить n букв з алфавіту , можна розглядати як n-граму

,

де , 0 i<n, для деякого цілого n=1, 2, 3, ... .

Позначимо множину n-грам, утворених з букв множини .

Криптографічне перетворення Е являє собою сукупність перетворень

.

Перетворення Е⁽ⁿ⁾ визначає, як кожна n-грама відкритого тексту замінюється n-грамою шифротексту , тобто , де 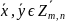, при цьому обов'язковою є вимога взаємної однозначності перетворення Е⁽ⁿ⁾ на множині .

Криптографічна система може трактуватися як сімейство криптографічних перетворень

,

позначених параметром K, який називається ключем.

Множина значень ключа утворює ключовий простір .

Підстановка в алфавіті є взаємно однозначним відображенням множини на , яке заміняє букву t відкритого тексту на букву шифротексту

де .

Множина всіх підстановок на називається симетричною групою і позначається .

Симетрична група має такі властивості:

1 Замкнутість. Добуток підстановок є підстановкою

.

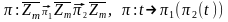2 Асоціативність. Обидва способи брати в дужки добуток підстановок дають однаковий результат

.

3 Існування одиничного елементу. Підстановка визначена як

є єдиним одиничним елементом групи по множенню

, для .

4 Існування зворотних елементів. Для кожної підстановки є взаємно однозначно визначена зворотна підстановка, яку позначають і яка задовольняє співвідношення

.

Усі розглянуті вище властивості є аксіомами групи.

Ключ K підстановки для алфавіту являє собою послідовність елементів симетричної групи з .

,

де

.

Підстановка, обумовлена ключем K, є криптографічним перетворенням , що шифрує n-граму

відкритого тексту в n-граму

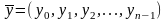
шифротексту, де

.

Криптографічне перетворення називається одноалфавітною підстановкою, якщо значення однакове для кожного i; у протилежному разі перетворення називається багатоалфавітною підстановкою.

На рис. 3.6 подана схема реалізації підстановки  .

Відзначимо характерні риси підстановки :

• відкритий текст шифрується побуквенно (буква за буквою);

• i-та буква y_i шифр текста є функцією тільки i-ї компоненти ключа та i-ї букви х_i відкритого тексту;

• шифрування n-грами виконується відповідно до формули

.

Рисунок 3.6 – Схема підстановки

3.2.1 Полібіанський квадрат

Одним з перших шифрів простої заміни вважається так званий полібіанський квадрат. За два століття до нашої ери грецький письменник-історик Полібій винайшов для цілей шифрування квадратну таблицю розміром 55, заповнену буквами грецького алфавіту у випадковому порядку (рис. 3.7).

Рисунок 3.7 – Полібіанський квадрат

При шифруванні в полібіанському квадраті знаходили букву відкритого тексту та записували в шифротекст букву, розміщену нижче у тому самому стовпці. Якщо буква відкритого тексту виявлялася в нижньому рядку таблиці, то для шифротексту брали верхню букву з того самого стовпця. Наприклад, для слова

   

одержимо такий шифротекст

    

Концепція полібіанського квадрата виявилася плідною і знайшла застосування в криптосистемах наступного часу.

3.2.2 Система шифрування Цезаря

Шифр Цезаря є окремим випадком шифру простої заміни (одноалфавітної підстановки). Шифр одержав свою назву від імені римського імператора Гая Юлія Цезаря, який використовував цей шифр при листуванні із Цицероном (близько 50 р. до н.е.).

При шифруванні вихідного тексту кожна буква замінялася на іншу букву того самого алфавіту за таким правилом. Буква для підстановки визначалася шляхом зсуву по алфавіту від букви відкритого тексту на позицій. При досягненні кінця алфавіту виконувався циклічний перехід до його початку. Цезар використав шифр із значенням K=3.

Наприклад, послання Цезаря ALEA JACTA EST («Жереб кинутий») для ключа K=3 у зашифрованому вигляді виглядає так: DOHD MDFWD HVW.

Таким чином, система Цезаря являє собою одноалфавітну підстановку, що шифрує n-граму відкритого тексту в n-граму 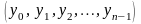шифротексту відповідно до такого правила:

де

j – числовий код букви відкритого тексту;

– числовий код відповідної букви шифротексту.

Система шифрування Цезаря утворює сімейство одноалфавітних підстановок для обраних значень ключа , причому .

Перевагою системи шифрування Цезаря є простота шифрування та розшифрування.

До недоліків системи Цезаря необхідно віднести такі:

• підстановки, що виконуються відповідно до системи Цезаря, не маскують частот появи букв вихідного відкритого тексту;

• зберігається алфавітний порядок у послідовності букв, якими замінюються букви відкритого тексту; при зміні значення змінюються тільки початкові позиції такої послідовності;

• число можливих ключів досить мале і обмежене кількістю букв алфавіту;

• шифр Цезаря легко розкривається на основі аналізу частот появи букв у шифротексті.

Криптоаналіз шифру Цезаря

Алгоритм злому шифру Цезаря можна виконати, використовуючи такий алгоритм:

1. Визначити частоти символів алфавіту. Занести їх у масив FiA.

2. Визначити частоти символів шифротексту. Занести їх у масив FiC:

а) обчислити скільки разів трапляється той або інший символ у шифротексті (занести в масив freq);

б) визначити кількість символів у шифротексті (l);

в) нормувати частоти символів, обчислені в пункті 2(a), результат помістити в масив FiC, тобто

.

3. Знайти таке значення k, при якому сума одноіменних різниць d була б мінімальною:

а) обчислити для всіх значень k=0, 1, … , 26 суми різниць

, де ;

б) знайти мінімальну суму різниць d;

в) запам'ятати значення k.

4. Розшифрувати шифротекст, використовуючи ключ k.

Алгоритм, що розглянуто вище, можна застосовувати до текстів англійської мови. Це пояснюється тим, що процес аналізу шифротексту виконувався за модулем 27 (26 літер латинського алфавіту та пропуск). У випадку аналізу шифрів інших мов необхідно змінити в залежності від кількості літер в алфавіті, що розглядається, значення модуля, за яким ведеться аналіз.

3.2.3 Аффінна система підстановок Цезаря

У системі шифрування Цезаря використовувалися тільки адитивні властивості множини цілих чисел . Однак елементи множини можна також множити за модулем m. Застосовуючи одночасно операції додавання та множення за модулем m над елементами множини , можна одержати систему підстановок, яку називають аффінною системою підстановок Цезаря.

Визначимо перетворення в такій системі:

де , 0 a<m, 0 b<m , .

У такому перетворенні літера, що відповідає числу t, замінюється літерою, що відповідає числовому значенню (at+b) за модулем m.

Слід помітити, що перетворення є взаємно однозначним відображенням на множині тільки в тому випадку, якщо числа а та m є взаємно простими.

Наприклад, візьмемо m = 26 (літери англійського алфавіту), а = 3, b = 5. Видно, НСД (3,26)=1. Отримаємо таку відповідність між числовими кодами букв:

Після відображення чисел в літери, отримуємо таку відповідність для літер відкритого тексту та шифротексту:

Таким чином, вихідне повідомлення FANCIFUL перетвориться в шифротекст UFSLDUNM

Перевагою аффінної системи є зручне керування ключами – ключі шифрування та розшифрування подаються в компактній формі у вигляді пари чисел (а, b). Недоліки аффінної системи аналогічні недолікам системи шифрування Цезаря.

3.2.4 Система Цезаря із ключовим словом

Система шифрування Цезаря із ключовим словом є одноалфавітною системою підстановки. Особливістю цієї системи є використання ключового слова для зсуву й зміни порядку символів в алфавіті підстановки.

Виберемо деяке число k, 0k<25, і слово або коротку фразу як ключове слово. Бажано, щоб всі букви ключового слова були різними. Однак ця вимога не є обов'язковою. Можна просто записати ключове слово (або фразу) без повторення однакових букв.

Нехай ключовим словом є слово «DIPLOMACY» і число k = 5.

Ключове слово записується під буквами алфавіту, починаючи з букви, числовий код якої збігається з обраним числом k:

Букви, що залишилися, алфавіту підстановки записуються після ключового слова за абеткою:

Маючи підстановку для кожної букви довільного повідомлення, легко виконати шифрування. Так вихідне повідомлення CHANGE DETALIES шифрується як WPUYIZ XZJUALZH.

Безсумнівною перевагою системи Цезаря із ключовим словом є те, що кількість можливих ключових слів практично невичерпна. Недоліком цієї системи є можливість злому шифротексту на основі аналізу частот появи букв.

3.2.5 Таблиці Трисемуса

В 1508 р. абат з Німеччини Йоганн Трисемус уперше описав застосування таблиць, що шифрують, заповненим алфавітом у випадковому порядку. Для одержання такого шифру заміни звичайно використовували таблицю для запису букв алфавіту та ключового слова (або фрази). У таблицю спочатку заносили по рядках ключове слово, причому букви, які повторюються, відкидалися. Потім ця таблиця доповнювалася буквами алфавіту, що ввійшли в неї з ключовим словом.

Оскільки ключове слово або фразу легко зберігати в пам'яті, то такий підхід спрощував процеси шифрування й розшифрування.

Розглянемо цей метод шифрування на прикладі. Для українського алфавіту таблиця, що шифрує, може мати розмір 48 (32 літери алфавіту). Виберемо як ключ слово “БАНДЕРОЛЬ”. Таблиця для шифрування має вигляд, поданий на рисунку 3.8.

Рисунок 3.8 – Таблиця для шифрування за методом Трисемуса з ключовим словом “БАНДЕРОЛЬ”

При шифруванні в таблиці знаходять чергову букву відкритого тексту й записують у шифротекст букву, розміщену нижче неї в тому самому стовпці. Якщо буква тексту виявляється в нижньому рядку таблиці, тоді для шифротексту беруть верхню букву з того самого стовпця.

Наприклад, при шифруванні за допомогою таблиці (рис. 3.8) повідомлення “МАГІСТРАЛЬ ЗРУЙНОВАНО”, одержимо шифротекст, записаний блоками по п’ять букв

ЧВКУЩ ЮЗВШЇ СЗЯХГ ИЙВГИ.

Такі табличні шифри називаються монограмними, тому що шифрування виконується по одній букві.

Криптографічний аналіз системи одноалфавітної заміни

Криптоаналіз системи одноалфавітної заміни, аналогічно шифру Цезаря, починається з підрахунку частот появи символів: визначається число появ кожної букви в шифротексті. Потім отриманий розподіл частот букв у шифротексті порівнюється з розподілом частот букв в алфавіті вихідних повідомлень, наприклад, в українському. Буква з найвищою частотою появи в шифротексті замінюється на букву з найвищою частотою появи в українській мові і т.д. Імовірність успішного розкриття системи шифрування підвищується зі збільшенням довжини шифротексту.

3.2.6 Біграмний шифр Плейфейра

Шифр Плейфейра (1854 р.), є найбільш відомим біграмним шифром заміни. Він застосовувався Великобританією під час Першої світової війни.

Основою шифру Плейфейра є таблиця, що шифрує, з випадково розміщеними буквами алфавіту вихідних повідомлень.

Для зручності запам'ятовування таблиці, що шифрує, відправник та одержувач повідомлень використовують ключове слово (або фразу) при заповненні початкових рядків таблиці. Загалом структура таблиці для шифрування системи Плейфейра повністю аналогічна структурі таблиці, що шифрує, Трисемуса. Тому для пояснення процедур шифрування й розшифрування в системі Плейфейра скористаємося таблицею шифрування Трисемуса (рис 3.8).

Процедура шифрування вміщує такі кроки:

1. Відкритий текст вихідного повідомлення розбивається на пари букв (біграми). Текст повинен мати парну кількість букв та не повинен містити біграми, що мають дві однакові букви. Якщо ці вимоги не виконані, то текст модифікується навіть через незначні орфографічні помилки.

2. Послідовність біграм відкритого тексту перетворюється за допомогою таблиці, що шифрує, у послідовність біграм шифротексту за такими правилами:

• якщо обидві літери біграми відкритого тексту не стоять в одному рядку або стовпці, наприклад, літери А і П (рис. 3.8), тоді знаходять літери в кутах прямокутника, обумовленого вихідною парою літер. У нашому прикладі це букви АЙПЕ. Пара літер АП відображається в пару ЙЕ. Послідовність літер у біграмі шифротексту повинна бути дзеркально розміщеною щодо послідовності літер у біграмі відкритого тексту;

• якщо обидві літери біграми відкритого тексту належать одному стовпцю таблиці, то за літери шифротексту беруть літери, які лежать під ними. Наприклад, біграма НК (рис 3.8) дає біграму шифротексту ГЦ. Якщо при цьому літера відкритого тексту стоїть в нижньому рядку, то для шифротексту береться відповідна літера з верхнього рядка того самого стовпця. Наприклад, біграма НЦ дає біграму шифротексту ГН;

• якщо обидві літери біграми відкритого тексту належать одному рядку таблиці, то літерами шифротексту вважаються букви, які знаходяться праворуч від них. Наприклад, біграма НО дає біграму шифротексту ДЛ. Якщо при цьому літера відкритого тексту знаходиться в крайньому правому стовпці, то для шифру беруть відповідну літеру з лівого стовпця у тому самому рядку. Так біграма ЕЛ дає біграму шифротексту РБ).

Виконаємо зашифрування тексту

ВСЕ ТАЄМНЕ СТАЄ ЯВНИМ.

Розіб’ємо текст на біграми

ВС ЕТ АЄ МН ЕС ТА ЄЯ ВН ИМ.

Дана послідовність біграм відкритого тексту перетворюється за допомогою таблиці для шифрування (рис. 2.9) в таку послідовність біграм шифротексту:

ЗЙ ОП ДВ КД РП ЙО ІЧ ГА ЄТ.

При розшифруванні застосовується зворотний порядок дій.

Слід зазначити, що шифрування біграмами різко підвищує стійкість шифрів до розкриття.

3.2.7 Криптосистема Хілла

Алгебраїчний метод, що узагальнює афінну підстановку Цезаря:

,

,

для визначення n-грам, був сформульований Лестером С. Хіллом.

Множина цілих чисел , для яких визначені операції додавання, віднімання та множення за модулем m, є кільцем.

Множина всіх n-грам =(x₀, x₁, x₂, …, x_n-1) з компонентами кільця утворить векторний простір над кільцем . Кожна n-грама називається вектором. У векторному просторі для векторів визначені операції додавання та віднімання за модулем m, а також скалярне множення вектора на елемент t кільця . Додавання і скалярне множення є операціями, що задовольняють комутативний, асоціативний та дистрибутивний закони.

Вектор є лінійною комбінацією векторів , якщо

. (3.1)

Лінійне перетворення є відображенням

,

, (3.2)

яке задовольняє умову лінійності

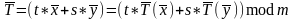
для всіх s, t та .

Лінійне перетворення може бути представлене матрицею розміром nn вигляду

, (3.3)

причому

або .

Базисом для векторного простору є набір векторів з , які лінійно незалежні і породжують . Кожен базис для містить n лінійно незалежних векторів. Довільний набір з n векторів, які лінійно незалежні над , є базисом.

Нехай є лінійним перетворенням, що описується матрицею (3.3), причому

.

Якщо вектори лінійно незалежні над , тоді їх образи лінійно незалежні над тільки в тому випадку, якщо визначник матриці не ділиться на будь-яке просте p, що ділить m. У цьому випадку перетворення називається невиродженим лінійним перетворенням, що має зворотне перетворення

,

_, (3.4)

де - одинична матриця. Крім того, також є лінійним перетворенням.

Для розшифрування n-грам шифротексту відновлення n-грам відкритого тексту необхідно виконати зворотне перетворення відповідно до рівняння

. (3.5)

Приклад. Виконати шифрування відкритого тексту DETERMINANT.

Маємо алфавіт , що складається із символів латинського алфавіту. Встановимо взаємно однозначну відповідність між алфавітом  і множиною цілих чисел .

Розглянемо матрицю Т= . Детермінант матриці =5 і модуль m=26 є взаємно простими числами, отже, матрицю Т можна використати як матрицю перетворення .

Виконаємо шифрування відкритого тексту. Розіб’ємо текст на біграми DE | TE | RM | IN | AN | TS і кожній біграмі поставимо у відповідність вектор, координатами якого є елементи множини

(3, 4) | (19, 4) | (17, 12) | (8, 13) | (0, 13) | (19, 18).

Щоб одержати шифротекст, перемножуємо матрицю перетворення на вектор кожної біграми.

DE:  RA,

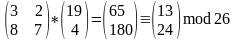
TE:  NY

і так далі.

У результаті отримаємо такі біграми шифротексту:

(17, 0) | (13, 24) | (23, 12) | (24, 25) | (0, 13) | (15, 18).

Звернувшись до встановленої відповідності отримаємо шифротекст RANYXMYZANPS.

Виконаємо розшифрування шифротексту RANYXMYZANPS.

Очевидно, що матрицею зворотного перетворення є

= .

Щоб одержати відкритий текст перемножуємо матрицю перетворення на вектор кожної біграми шифротексту.

RA: *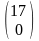 = DE,

NY: * = TE

і так далі.

Виконавши всі перетворення, переконаємося, що з шифротексту RANYXMYZANPS дійсно отримали відкритий текст DETERMINANT.

3.2.8 Система омофонів

Система омофонів забезпечує найпростіший захист від криптоаналітичних атак, заснованих на підрахунку частот появи літер у шифротексті. Система омофонів є одноалфавітною, хоча при цьому літери вихідного повідомлення мають кілька замін. Число замін береться пропорційним до імовірності появи літери у відкритому тексті.

Дані про розподіли ймовірностей літер у російському та англійському текстах наведені в таблицях 1 і 2 додатка A відповідно. Букви в таблицях зазначені в порядку спадання ймовірності появи їх у тексті. Наприклад, російська літера О трапляється у 30 разів частіше, ніж літера Щ, а англійська літера Е – в 123 рази частіше, ніж літера Z.

Шифруючи букву вихідного повідомлення, вибирають випадковим образом одну з її замін. Заміни, які часто називають омофонами, можуть бути представлені трb розрядними числами від 000 до 999. Наприклад, в англійському алфавіті букві Е привласнюються 123 випадкові номери, буквам У и G – по 16 номерів, а буквам J й Z – по 1 номеру. Якщо омофони (заміни) привласнюються випадково різним появам однієї й тієї самої букви, тоді кожен омофон трапляється в шифротексті з однаковою ймовірністю.

При такому підході до формування шифротексту простий підрахунок частот уже нічого не дає криптоаналітику. Однак у принципі корисна також інформація про розподіл пар і трійок букв у різних природних мовах. Якщо цю інформацію використати в криптоаналізі, він буде проведений більш успішно.

3.3 Шифри складної заміни

Шифри складної заміни називають багатоалфавітними тому, що для шифрування кожного символа вихідного повідомлення застосовують свій шифр простої заміни.

Багатоалфавітна підстановка послідовно й циклічно змінює використовувані алфавіти.

При r-алфавітній підстановці символ вихідного повідомлення замінюється символом з алфавіту , символ  – символом 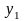з алфавіту і т. д., символ заміняється символом з алфавіту .

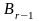Загальна схема багатоалфавітної підстановки для випадку наведена в таблиці 1.

Таблиця 1

Ефект використання багатоалфавітної підстановки полягає в тому, що забезпечується маскування природної статистики вихідної мови, тому що конкретний символ з вихідного алфавіту А може бути перетворений у кілька різних символів шифрувальних алфавітів , . Ступінь забезпечуваного захисту теоретично пропорційна довжині періоду r у послідовності використовуваних алфавітів .

Багатоалфавітні шифри заміни запропонував та ввів у практику криптографії Ліон Баттіста Альберті, що також був відомим архітектором і теоретиком мистецтва. Його книга «Трактат про шифр», написана в 1566 р., являла собою першу у Европі наукову працю з криптології. Крім шифру багатоалфавітної заміни, Альберті також докладно описав пристрій з обертових колес для його реалізації. Криптологи всього світу вважають Л. Альберті основоположником криптології.

3.3.1 Шифр Гронсфельда

Шифр складної заміни, який називають шифром Гронсфельда, являє собою модифікацію шифру Цезаря за допомогою числового ключа. Для цього під літерами вихідного повідомлення записують цифри числового ключа. Якщо ключ коротший за повідомлення, то його запис циклічно повторюють.

Літерою шифротексту вважають літеру, яка зміщена за алфавітом на число позицій, відповідне цифрі ключа.

Наприклад, застосовуючи як ключ натуральне число 2718, одержимо для вихідного повідомлення ТАЄМНИЙ КЛЮЧ такий шифротекст:

Щоб зашифрувати першу букву повідомлення Т, використовуючи першу цифру ключа 2, потрібно відрахувати другу літеру від Т у алфавіті

виходить перша літера шифротексту Ф.

Криптоаналіз шифру Гронсфельда

Слід зазначити, що шифр Гронсфельда розкривається відносно легко, якщо врахувати, що в числовому ключі кожна цифра має тільки десять значень, виходить, є лише десять варіантів прочитання кожної літери шифротексту. З іншого боку, шифр Гронсфельда допускає подальші модифікації, що поліпшують його стійкість, зокрема, подвійне шифрування різними числовими ключами.

3.3.2 Система шифрування Віженера

Шифр Гронсфельда являє собою, власне кажучи, окремий випадок системи шифрування Віженера.

Система Віженера вперше була опублікована в 1586 р. і є однією з найстаріших і найбільш відомих багатоалфавітних систем. Система шифрування була названа ім’ям французького дипломата XVI століття Блеза Віженера, що розвивав і удосконалював криптографічні системи.

Система Віженера подібна до системи шифрування Цезаря, за тим винятком, що ключ підстановки змінюється від літери до літери. Шифр багатоалфавітної заміни можна описати таблицею шифрування, яку часто називають таблицею Віженера. У додатку Б наведені таблиці Віженера для англійського, українського та російського алфавітів.

Таблиця Віженера використовується для зашифрування та розшифрування. Таблиця має два входи:

• верхній рядок символів, який використовується для зчитування літери вихідного відкритого тексту;

• крайній лівий стовпець ключа, який використовується для зчитування літери ключа.

При шифруванні вихідного повідомлення його виписують у рядок, а під ним записують ключове слово (або фразу). Якщо ключ виявився коротший за повідомлення, то його циклічно повторюють. У процесі шифрування знаходять у верхньому рядку таблиці чергову літеру вихідного тексту, а у лівому стовпці – чергове значення ключа. Літеру шифротексту знаходять на перетинанні стовпця, обумовленого літерою, що шифрують, та рядка, обумовленого відповідною літерою ключа.

Нехай ключова послідовність має довжину r, тоді ключ r-алфавітної підстановки є r-рядок

_.

Система шифрування Віженера перетворить відкритий текст 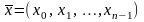у шифротекст за допомогою ключа відповідно до правила

_,

де

_, .

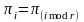Наприклад, з використанням шифру Віженера виконати шифрування відкритого тексту М= “БЕЗ КАЛИНИ НЕМА УКРАЇНИ” ключем Key =“БАРВІНОК”.

Випишемо вихідне повідомлення в рядок і запишемо під ним ключове слово з циклічним повторенням. У третій рядок будемо виписувати літери шифротексту, обумовлені таблицею Віженера (таблиця 2 дадатка Б).

У результаті отримаємо шифротекст, що записано блоками по п'ять букв

ВЕЩМІ ЯШЮІН ЦОІЄЯ ББЇҐЇ.

Іноді, використовуючи шифр Віженера, можна обійтися і без таблиць для шифрування. Для цього кожному символу відкритого тексту та ключа ставляться у відповідність натуральні числа, які відповідають їхнім номерам в алфавіті, що розглядається. Далі знаходять попарно суми за модулем m, де m – кількість літер у алфавіті.

Наприклад, виконаємо шифрування без використання таблиць Віженера.

Будемо розглядати український алфавіт (m=33). Поставимо у відповідність кожному символу алфавіту ціле натуральне число, інакше кажучи, пронумеруємо символи алфавіту, починаючи з нуля.

Записуємо під кожним символом відкритого тексту символ ключового слова в циклічному порядку. Потім складаємо числа, що відповідають номерам літер відкритого тексту, із числами, що відповідають номерам літер ключа за модулем 33.

У результаті одержимо той самий шифротекст, що й у випадку використання таблиць Віженера:

ВЕЩМІ ЯШЮІН ЦОІЄЯ ББЇҐЇ .

3.3.3 Шифр “Подвійний квадрат Уітстона”

У 1854 р. англієць Чарльз Уітстон розробив новий метод шифрування біграмами, що називають «подвійним квадратом». Шифр Уітстона відкрив новий етап в історії розвитку криптографії. На відміну від полібіанського подвійний квадрат використовує відразу дві таблиці, розміщені по горизонталі, а шифрування виконується біграмами, як і у шифрі Плейфейра. Ці нескладні модифікації привели до появи якісно нової криптографічної системи ручного шифрування. Шифр Уітстона виявився дуже надійним і зручним у застосовуванні. Шифр використовувався Німеччиною навіть у роки Другої світової війни.

Розглянемо докладніше процедуру шифрування. Створюються дві таблиці з випадково розміщеними символами алфавіту. Перед шифруванням вихідне повідомлення розбивають на біграми. Кожна біграма шифрується окремо.

Першу літеру біграми знаходять у лівій таблиці, а другу – у правій таблиці. Потім будують уявний прямокутник так, щоб літери біграми знаходились у його протилежних вершинах. Інші дві вершини цього прямокутника дають літери біграми шифротексту.

Якщо обидві літери біграми повідомлення розміщені в одному рядку, то й літери шифротексту беруть із цього самого рядка. Першу літеру біграми шифротексту беруть із лівої таблиці в стовпці, що відповідає другій літері біграми повідомлення. Друга літера біграми шифротексту береться із правої таблиці в стовпці, що відповідає першій літері біграми повідомлення.

Наприклад, використовуючи подвійний квадрат Уітстона, зашифрувати повідомлення «НЕ ЦУРАЙТЕСЬ ТОГО СЛОВА, ЩО МАТИ СПІВАЛА».

Будемо розглядати український алфавіт, який доповнимо символами “.” (крапка), “,” (кома) та “_” (пропуск). Разом алфавіт буде містити 36 символів. Отож візьмемо таблиці розміром 66 (рис. 3.9).

Рисунок 3.9 – Таблиці для шифру “Подвійний квадрат Уітстона”

Розбиваємо текст на біграми:

НЕ | _Ц | УР | АЙ | ТЕ | СЬ |  _Т | ОГ | О_ | СЛ | 

ОВ | А, | _Щ | О_ | МА | ТИ | _С | ПІ | ВА | ЛА

Відповідно до алгоритму виконаємо відповідні перетворення:

Отже, маємо шифротекст, записаний блоками по 5 символів:

ФГХЦЙ ,ЬЦЄК РЧНЦЦ ЇГТЩД

ЕРВ.Н ИГТМЯ ПЕЇПС .ЧРУЯ .

Розшифрування виконується так само, як і шифрування. Єдина відмінність полягає в тому, що при розшифруванні таблиці міняються місцями (рис. 3.10).

Шифрування методом подвійного квадрата досить стійкий до розкриття та простий у застосуванні шифр.

Рисунок 3.10 – Таблиці для розшифрування в шифрі “Подвійний квадрат Уітстона”

3.3.4 Одноразова система шифрування

Майже всі шифри, що застосовуються на практиці, характеризуються як умовно надійні, оскільки вони можуть бути в принципі розкриті при наявності необмежених обчислювальних можливостей. Абсолютно надійні шифри не можна зруйнувати навіть при використанні необмежених обчислювальних можливостей. Існує єдиний такий шифр, який застосовується на практиці, - одноразова система шифрування. Характерною рисою одноразової системи шифрування є одноразове використання ключової послідовності.

Одноразова система шифрує вихідний відкритий текст у шифротекст за допомогою підстановки

_, (3.6)

де – i-й елемент випадкової ключової послідовності.

Ключовий простір одноразової системи являє собою набір дискретних випадкових величин з і містить mⁿ значень.

Процедура розшифрування описується співвідношенням (3.7)

, (3.7)

де

– i-й елемент тієї самої випадкової ключової послідовності.

Одноразову систему було винайдено в 1917 р. американцями Дж. Моборном і Г. Вернамом. Для реалізації цієї системи підстановки іноді використовують одноразовий блокнот. Цей блокнот складається з відривних сторінок, на кожній з яких надрукована таблиця з випадковими числами (ключами) . Блокнот виконується у двох екземплярах: один використовується відправником, а інший - одержувачем. Для кожного символа повідомлення використовується свій ключ з таблиці тільки один раз. Після того як таблиця була використана, вона повинна бути вилучена із блокнота та знищена. Шифрування нового повідомлення починається з нової сторінки.

Цей шифр абсолютно надійний, якщо набір ключів дійсно випадковий і непередбачений. Якщо криптоаналітик спробує використати для заданого шифротексту всі можливі набори ключів і відновити всі можливі варіанти вихідного тексту, то вони всі матимуть однакову ймовірність. Не існує способу вибрати вихідний текст, що був дійсно посланий. Теоретично доведено, що одноразові системи не можуть бути розкриті без ключа, оскільки шифротекст не містить достатньої інформації для відновлення відкритого тексту.

На перший погляд здається, що завдяки абсолютній стійкості одноразової системи варто було б застосовувати її у всіх випадках, що вимагають абсолютної інформаційної безпеки. Однак можливості застосування одноразової системи обмежені лише практичними аспектами. Істотним моментом є вимога одноразового використання випадкової ключової послідовності. Ключова послідовність із довжиною, не меншої довжини повідомлення, повинна передаватися одержувачу повідомлення заздалегідь або окремо по деякому секретному каналу зв’язку. Ця вимога не буде занадто обтяжною для передавання дійсно важливих одноразових повідомлень. Однак така вимога практично нездійсненна для сучасних систем обробки інформації, де потрібно шифрувати багато мільйонів символів.

У деяких варіантах одноразового блокнота удаються до більш простого керування ключовою послідовністю, але це приводить до деякого зниження надійності шифру. Наприклад, ключ визначається вказівкою місця в книзі, відомої відправникові й одержувачеві повідомлення. Ключова послідовність починається із зазначеного місця цієї книги й використовується в такий самий спосіб, як у системі Віженера. Іноді такий шифр називають шифром із ключем, що біжить. Керування ключовою послідовністю в такому випадку набагато простіше, тому що довга ключова послідовність може бути представлена в компактній формі. Але з іншого боку, ці ключі не будуть випадковими. Тому у криптоаналітика з'являється можливість використати інформацію про частоти букв вихідної природної мови.

3.3.5 Шифрування методом Вернама

Значний внесок у розвиток криптографії зробив американець Г. Вернам. У 1917 році він, будучи співробітником телеграфної компанії, запропонував ідею автоматичного шифрування телеграфних повідомлень, суть якої полягає в наступному.

Відкритий текст представляється в коді Бодо (у вигляді п'ятизначних імпульсних комбінацій). У цьому коді, наприклад, буква «А» мала вигляд (+ + – – –). На паперовій стрічці ця буква одержувала такий вигляд (рис. 3.11) .

Знак «+» означав отвір, а знак «-» – його відсутність. При зчитуванні зі стрічки п'ятірка металевих щупів «пізнавала» отвір (при наявності отвору щуп замикав електричний ланцюг) і на лінії зв'язку посилався імпульс струму (рис. 3.12).

Рисунок 3.11 – Паперова стрічка системи Вернама

Рисунок 3.12 – Імпульс струму в системі Вернама

Вернам запропонував електромеханічно покоорди-натно додавати імпульси знаків секретного тексту з імпульсами гами.

Гама – це секретний ключ, що представляє хаотичний набір літер того самого алфавіту.

Додавання здійснювалося за модулем 2.

0  0 = 0,

0  1 = 1,

1  0 = 1,

1  1 = 0 ,

де

 – операція додавання за модулем 2,

0 – знак «-» коду Бодо,

1 – знак «+» коду Бодо.

Нехай, наприклад, знак гами має вигляд

+ – + – – (10100).

Тоді буква «А» при шифруванні переходить у двійкову комбінацію 01100 (– + + – –).

При розшифруванні необхідно повторити покоординатно ту саму операцію

(01100)  (10100) = (11000) = А.

Схема шифрування методом Вернама подана на рисунку 3.13

Рисунок 3.13 – Схема шифрування та розшифрування повідомлень методом Вернама

Вернам створив пристрій, що робить зазначені операції автоматично, без участі шифрувальника. Тим самим дав початок лінійному шифруванню, коли процеси шифрування та передачі повідомлення відбуваються одночасно. До цього шифрування було попереднім, тому лінійне шифрування істотно підвищувало оперативність зв'язку.

Відзначимо одну важливу особливість шифру Вернама, що послужила надалі обґрунтуванню теорії досконалого шифру, яку було запропоновано американським класиком криптографії К. Шенноном. Справа в тому, що при застосуванні шифру Вернама за перехопленим шифрованим текстом видгляу  може ховатися будь-який відкритий текст  . Будь-якому відкритому тексту можна підібрати гаму, що породжує даний шифрований текст. Оскільки гама є ключем, то за перехопленням шифрованого повідомлення неможливо відкинути жодного відкритого тексту тієї самої довжини. Зусилля дешифровальників зводяться на “ні”.

Шифр Вернама має виняткову криптографічну стійкість. У той самий час стає ясним і недолік цієї системи шифрування. Хаотична гама (ключ) повинна мати ту саму довжину, що й відкритий текст. Для розшифрування на кінець лінії зв'язку, що приймає інформацію, необхідно передати (по таємних, захищених каналах) гаму достатньої довжини. При практичній реалізації це породжує істотні проблеми, причому досить істотні, що й визначило досить скромне поширення шифрів Вернама.

У цій ситуації був запропонований простий вихід: гама шифру записувалася на стрічку, склеєну в кільце. Таким чином, вона ставала не випадковою, а періодичною (як у шифрі Віженера). Шифр ставав нестійким.

Сам Вернам не був математиком-криптографом. Проте він наполягав на тому, що гама шифру не повинна повторюватися при шифруванні, і в цьому він був правий. Його ідеї покладені в основу нових підходів до надійного захисту інформації при передаванні значних за обсягом повідомлень.

3.4 Блочні шифри

Характерною особливістю блочних криптоалгоритмів є той факт, що в процесі своєї роботи вони проводять перетворення блоку вхідної інформації фіксованої довжини і одержують результуючий блок того самого об'єму, але недоступний для прочитання стороннім особам, які не володіють ключем шифрування. Таким чином, схему роботи блокового шифру можна описати функціями:

,

.

Ключ є параметром блокового криптоалгоритму і являє собою деякий блок двійкової інформації фіксованого розміру. Початковий і зашифрований блоки даних також мають однакову фіксовану розрядність, але необов'язково таку, що дорівнює довжині ключа.

Блокові шифри є основою, на якій реалізовані практично всі криптосистеми. Методика створення ланцюжків із зашифрованих блоковими алгоритмами байтів дозволяє шифрувати ними пакети інформації необмеженої довжини. Така властивість блокових шифрів, як швидкість роботи, використовується асиметричними криптоалгоритмами, повільними за своєю природою. Відсутність статистичної кореляції між бітами вихідного потоку блокового шифру використовується для обчислення контрольних сум пакетів даних і в хешуванні паролів.

Криптоалгоритм іменується ідеально стійким, якщо прочитати зашифрований блок даних можна тільки перебравши всі можливі ключі, до тих пір, поки повідомлення не виявиться осмисленим. Оскільки за теорією вірогідності шуканий ключ буде знайдений з вірогідністю 0,5 після перебору половини всіх ключів, то на злом ідеально стійкого криптоалгоритму з ключем довжини буде потрібно в середньому перевірка. Таким чином, в загальному випадку стійкість блокового шифру залежить тільки від довжини ключа і зростає експоненціально з її зростанням. Окрім цієї умови до ідеально стійких криптоалгоритмів застосовується ще одна дуже важлива вимога, якій вони повинні обов'язково відповідати. При відомих початковому і зашифрованому значеннях блоку ключ, яким проведене це перетворення, можна дізнатися також тільки повним перебором. Ситуації, в яких сторонньому спостерігачу відома частина початкового тексту зустрічаються повсюди. Це можуть бути стандартні написи в електронних бланках, фіксовані заголовки форматів файлів, що досить часто трапляються в тексті довгі слова або послідовності байтів. У світлі цієї проблеми описана вище вимога не є надмірною і також строго виконується стійкими криптоалгоритмами, як і перша.

Таким чином, на функцію стійкого блочного шифру накладаються такі умови:

1. Функція повинна бути зворотною.

2. Не повинно існувати інших методів прочитання повідомлення по відомому блоку , окрім як повним перебором ключів .

3. Не повинно існувати інших методів визначення яким ключем було проведене перетворення відомого повідомлення в повідомлення , окрім як повним перебором ключів.

3.4.1 Алгоритм des

Американський стандарт криптографічного захисту даних (Data Encryption Standard), прийнятий в 1978 році є типовим представником сімейства блочних шифрів. Цей шифр допускає ефективну апаратну та програмну реалізації, причому можливо досягнення швидкостей до декількох мегабайтів за секунду.

Алгоритм DES виконує шифрування 64-бітних блоків даних за допомогою 56 бітного ключа. Дешифрування в DES є оберненою операцією шифруванню і виконується шляхом повторення операцій шифрування в зворотній послідовності.

Процес шифрування полягає в початковій перестановці 64 бітів вхідного блоку, шістнадцяти циклах шифрування та зворотній перестановці бітів (рис. 3.15)

Необхідно звернути увагу на те, що всі таблиці алгоритму DES є стандартними і повинні включатися в реалізацію алгоритму в незмінному вигляді. Усі перестановки і коди в таблицях підібрані так, щоб зробити максимально важким процес зламування шляхом підбору ключа.

Рисунок 3.15 – Загальна схема процесу шифрування в алгоритмі DES

Розглянемо алгоритм докладніше. Припустимо, з файлу зчитано 64-бітний блок , який перетворюється за допомогою початкової перестановки IP (рис. 3.16) в 64-бітний блок .

Рисунок 3.16 – Матриця початкової перестановки

Після IP-перестановки 16 разів повторюється процедура шифрування блока за допомогою функції . Позначимо

– результат i-ї ітерації;

– перші (ліві) 32 біти блоку , ;

– останні (праві) 32 біти блоку , .

Таким чином,

.

Тоді результатом i-ї операції буде:

,

,

де

– операція додавання за модулем 2;

– i-те перетворення ключа шифрування .

Функція виконує операції над значенням (результатом минулої операції) та поточним значенням 48-бітного ключа (з відокремленням зайвих бітів). До речі, після 16-ї ітерації ліва і права половини блока не міняються місцями (рис. 3.17). По закінченні шифрування виконується відновлення позицій бітів за допомогою матриці перестановок (рис. 3.18).

Розглянемо докладніше функцію .

Крок 1 На кожній ітерації масив розширюється до 48 бітів за допомогою таблиці розподілення бітів . Блок розбивається на вісім блоків по 4 біти (рис. 3.19).

Рисунок 3.17 – Загальна схема алгоритму шифрування DES

Шляхом копіювання крайніх елементів вісім 4-бітних блоки перетворюються у вісім 6-бітних блоків (рис. 3.20). Отриманий блок має 48 бітів.

Крок 2 Блок порозрядно сумують за модулем 2 з поточним значенням ключа , а потім розбивають на вісім 6-бітних блоки , тобто .

Крок 3 Кожен блок ( ) подається на вхід підстановки S-бокс (рис 3.21). Індекс вказує, який з масивів S-боксу використовувати. Застосувавши операцію вибору до кожного із блоків , одержимо 32-бітний потік.

Рисунок 3.20 – Таблиця розподілення бітів

Відзначимо, що вибір елемента в масиві здійснюється досить оригінальним способом. Нехай на вхід подається 6-бітний блок , дві крайні позиції інтерпретуються як двійкове подання цілих чисел з набору {0, 1, 2, 3}.

Рисунок 3.21 – S-бокс

Ці числа визначають номер рядка (від 0 до 3) масиву . Чотири біти, що залишилися, інтерпретуються як двійкове подання цілих чисел з набору {0, 1, 2, … , 15} і використовуються для визначення стовпця (від 0 до 15) у масиві .

Таким чином, вхідний блок, наприклад, , відповідає десятковому числу 9, розміщеному в другому рядку та в третьому стовпці масиву , Число 9 у двійковому поданні являє собою 4-бітний блок (1001).

У результаті застосувавши до кожного з блоків (  ) операцію вибору в S-боксі, одержимо 32-бітний блок

.

Крок 4 Отриманий блок перетворюється за допомогою матриці перестановки (рис. 3.22).

Рисунок 3.22 – Матриця перестановки

Таким чином,

_.

Обчислення значень ключів

Ще раз відзначимо, що на кожній ітерації використовується нове значення ключа , яке обчислюється із початкового значення ключа . Ключ _K – 64-бітний блок з вісьмома бітами контролю парності, що розміщені в позиціях 8, 16, 24, 32, 40, 48, 56, 64.

Для видалення контрольних бітів і підготовки ключа до роботи використовується матриця (рис. 3.23).

Рисунок 3.23 – Матриця попередньої

підготовки ключа

Результат перетворення розбивається на дві половини та по 28 бітів кожна. Після цього блоки та на кожній ітерації послідовно зміщуються вліво. Нехай та позначають значення, які отримані в результаті i-ї операції:

де – i-й елемент матриці здвигу (рис. 3.24).

Рисунок 3.24 – Матриця здвигу для обчислення ключа

Отримане значення знову “перемішується” у відповідності до матриці (рис. 3.25).

Рисунок 3.25 – Матриця кінцевої обробки ключа

Схема алгоритму обчислення ключа наведена на рисунку 3.26.

Рисунок 3.26 – Схема алгоритму генерації ключа

Відзначимо, що відновлення вихідного тексту виконується за допомогою такої самої послідовності дій, що й при шифруванні, але (!) спочатку використовують ключ і т.д.

Аналіз ефективності алгоритму des

Оскільки довжина блоків вихідного тексту дорівнює 64, підтримка каталогів частот використання блоків є для зловмисника завданням, що виходить за межі сучасних технічних можливостей.

Однак даний алгоритм має ряд недоліків. За час, що пройшов після створення DES, комп'ютерна техніка розвинулася настільки швидко, що виявилося можливим здійснювати вичерпний перебір ключів і тим самим розкривати шифр. Вартість цієї атаки постійно знижується. В 1998 р. була побудована машина вартістю близько 100 тис. доларів, здатна по даній парі (вихідний текст, шифрований текст) відновити ключ за середній час 3 доби. Таким чином, при стандартному використанні алгоритм DES став далеко не оптимальним вибором для задоволення вимогам таємності даних.

Була висунута велика кількість пропозицій по вдосконаленню алгоритму DES, які частково компенсують зазначені недоліки.

4 Асиметричні криптосистеми

4.1 Концепція криптосистеми з відкритим ключем

Ефективними системами криптографічного захисту даних є асиметричні криптосистеми, які називають також криптосистемами з відкритим ключем. У таких системах для зашифрування даних використовується один ключ, а для розшифрування – інший ключ (звідси й назва – асиметричні). Перший ключ є відкритим і може бути опублікований для використання всіма користувачами системи, які зашифровують дані. Розшифрувати дані за допомогою відкритого ключа неможливо.

Для розшифрування даних одержувач зашифрованої інформації використовує другий ключ, що є таємним. Зрозуміло, таємний ключ не може бути визначений, виходячи з відкритого ключа.

Узагальнена схема криптосистеми з відкритим ключем показана на рисунку 4.1. В цій криптосистемі застосовують два різних ключі: – відкритий ключ відправника A; – таємний ключ одержувача В.

Генератор ключів доцільно розташовувати на стороні одержувача B, щоб не пересилати таємний ключ незахищеним каналом. Значення ключів і залежать від початкового стану генератора ключів.

Розкриття таємного ключа за значенням відомого відкритого ключа повинно бути обчислювально нерозв’язаною задачею.

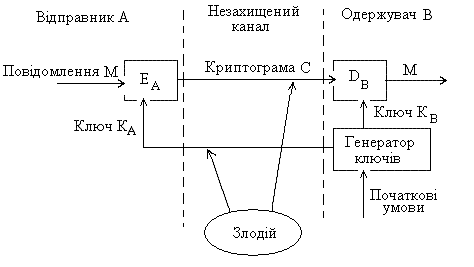
Рисунок 4.1 – Узагальнена схема асиметричної криптосистеми

Характерні риси асиметричних криптосистем:

1. Відкритий ключ і криптограма C можуть бути відправлені по незахищених каналах, тобто зловмиснику відомі значення та C.

2. Алгоритми шифрування ( ) і розшифрування є відкритими.

Захист інформації в асиметричній криптосистемі засновано на таємності ключа .

У.Діффі та М.Хеллман сформулювали вимоги, які забезпечують безпеку асиметричної криптосистеми:

1. Обчислення пари ключів ( ,  ) одержувачем B на основі початкової умови повинно бути простим.

2. Відправник A, знаючи відкритий ключ і повідомлення М, може легко обчислити криптограму

. (4.1)

3 Одержувач В, використовуючи таємний ключ і криптограму C, може легко відновити вихідне повідомлення

. (4.2)

4 Зловмисник, знаючи відкритий ключ , при спробі обчислити таємний ключ натрапляє на непереборну обчислювальну проблему.

5 Зловмисник, знаючи пари ( , C), при спробі обчислити вихідне повідомлення M натрапляє на непереборну обчислювальну проблему.

4.2 Односпрямовані функції

Концепція асиметричних криптографічних систем з відкритим ключем заснована на застосуванні односпрямованих функцій. Неформально односпрямовану функцію можна визначити в такий спосіб.

Нехай Х і Y – деякі довільні множини. Функція є односпрямованою, якщо для всіх можна легко обчислити функцію , але для більшості досить складно одержати значення , таке, що (при цьому вважають, що існує принаймні одне таке значення ).

Основним критерієм віднесення функції до класу односпрямованих функцій є відсутність ефективних алгоритмів зворотного перетворення .

Як приклад односпрямованої функції розглянемо множення цілих чисел. Пряма задача – обчислення добутку двох дуже великих цілих чисел й , тобто знаходження значення

(4.3)

є простою задачею для ЕОМ.

Зворотна задача – розкладання на множники великого цілого числа, тобто знаходження дільників і великого цілого числа , є практично нерозв’язною задачею при досить великих значеннях .

За сучасними оцінками теорії чисел при цілому й для розкладання числа буде потрібно близько 10²³ операцій, тобто задача практично нерозв’язна.

Наступний характерний приклад односпрямованої функції – це модульна експонента з фіксованими підставою й модулем. Нехай й – цілі числа, такі, що . Визначимо множину

.

Тоді модульна експонента з основою за модулем N являє собою функцію

,

де – ціле число, .

Існують ефективні алгоритми, що дозволяють досить швидко обчислити значення функції .

Якщо , то, природно, .

Тому, задачу обернення функції називають задачею знаходження дискретного логарифма або задачею дискретного логарифмування.

Задача дискретного логарифмування формулюється в такий спосіб.

Для відомих цілих знайти ціле число , таке, що

.

Алгоритм обчислення дискретного логарифма за прийнятний час поки не знайдена, тому модульна експонента вважається односпрямованою функцією.

За сучасними оцінками теорії чисел при досить великих цілих числах A2⁶⁶⁴ й N2⁶⁶⁴ рішення задачі дискретного логарифмування (знаходження показника ступеня для відомого ) потребує близько 10²⁶ операцій, тобто ця задача має в 10³ разів більшу обчислювальну складність, ніж задача розкладання на множники. Різниця в оцінках складності задач зростає при збільшенні довжини чисел.

Відзначимо, що поки не вдалося довести, що не існує ефективного алгоритму обчислення дискретного логарифма за прийнятний час. Виходячи з цього, модульна експонента віднесена до односпрямованих функцій умовно, що однак не заважає з успіхом застосовувати її на практиці.

Другим важливим класом функцій, що використовуються при побудові криптосистем з відкритим ключем, є односпрямовані функції з "потаємним ходом".

Функція належить до класу односпрямованих функцій з "потаємним ходом" у тому випадку, якщо вона є односпрямованою й, крім того, можливо ефективне обчислення зворотної функції, якщо відомо "потаємний хід" (таємне число, рядок або інша інформація, що асоціюється з даною функцією).

Як приклад односпрямованої функції з "потаємним ходом" можна вказати модульну експоненту з фіксованими модулем і показником ступеня, що використовується в криптосистемі RSA. Змінна основа модульної експоненти використовується для вказівки числового значення повідомлення М або криптограми С.

4.3 Криптосистема шифрування даних RSA

Алгоритм RSA запропонували в 1978 р. Р.Райвест (Rivest), А.Шамір (Shamir) і А.Адлеман (Adleman). Алгоритм одержав свою назву від перших букв прізвищ його авторів. Алгоритм RSA став першим повноцінним алгоритмом з відкритим ключем, що може працювати як у режимі шифрування даних, так і у режимі електронного цифрового підпису.

Надійність алгоритму ґрунтується на труднощі факторизації великих чисел і труднощі обчислення дискретних логарифмів.

У криптосистемі RSA розглядають: відкритий ключ ; таємний ключ ; повідомлення й криптограма належать множині цілих чисел

, (4.4)

де - модуль

. (4.5)

Тут й – випадкові великі прості числа. Для забезпечення максимальної безпеки вибирають і однакової довжини й зберігають у секреті.

Множина з операціями додавання та множення за модулем утворює арифметику за модулем .

Відкритий ключ вибирають випадково так, щоб виконувалися умови:

(4.6)

, (4.7)

де – функція Ейлера.

Функція Ейлера вказує кількість додатних цілих чисел в інтервалі від 1 до , які взаємно прості з N

.

Умова (3.7) означає, що відкритий ключ і функція Ейлера повинні бути взаємно простими.

Далі, використовуючи розширений алгоритм Евкліда, обчислюють таємний ключ , такий, що

(4.8)

або

.

Це можна здійснити, тому що одержувач B знає пару простих чисел і може легко знайти . Помітимо, що й повинні бути взаємно простими.

Відкритий ключ використовують для шифрування даних, а таємний ключ – для розшифрування.

Процес зашифрування визначає криптограму через пару ( , М) у відповідності до формули (4.9).

(4.9)

Обернення функції , тобто визначення значення M за відомим значенням практично не здійсненне при N2⁵¹².

Однак обернену задачу, тобто задачу розшифрування криптограми C, можна вирішити, використовуючи пару ( ,  ) за формулою (4.10).

. (4.10)

Процес розшифрування можна записати так:

(4.11)

Підставляючи в (4.11) значення (4.9) і (4.10), одержуємо:

або

. (4.12)

Відповідно до теореми Ейлера, яка стверджує, що якщо , то

або

. (4.13)

Порівнюючи вираження (4.12) і (4.13), одержуємо

або, що те саме,

.

Саме тому для обчислення таємного ключа використовують співвідношення (4.8).

Таким чином, якщо криптограму

піднести до степеня , то в результаті відновлюється вихідний відкритий текст М, тому що

.

Отже, одержувач B, що створює криптосистему, захищає два параметри: таємний ключ і пару чисел , добуток яких дає значення модуля N. З іншого боку, одержувач B відкриває значення модуля N і відкритий ключ .

Зловмиснику відомі лише значення та N. Якби він зміг розкласти число N на множники P й Q, то він довідався б "потаємний хід" – трійку чисел , обчислив значення функції Ейлера та визначив значення таємного ключа .

Однак, як було відзначено раніше, розкладання дуже великого числа N на множники не здійсненно обчислювальними методами (за умови, що довжини обраних Р и Q становлять не менше 100 десяткових знаків).

Процедури шифрування та розшифрування в криптосистемі RSA

Припустимо, що користувач A хоче передати користувачеві B повідомлення в зашифрованому вигляді, використовуючи криптосистему RSA. У такому випадку користувач A є в ролі відправника повідомлення, а користувач B – у ролі одержувача. Як відзначалося вище, криптосистему RSA повинен сформувати одержувач повідомлення, тобто користувач В. Розглянемо послідовність дій користувача В і користувача A.

1. Користувач B вибирає два довільних великих простих числа P й Q.

2. Користувач B обчислює значення модуля N згідно з (4.5).

3. Користувач B обчислює функцію Ейлера й вибирає значення відкритого ключа з урахуванням виконання умов (4.6) і (4.7).

4. Користувач B обчислює значення таємного ключа за формулою (4.8), використовуючи розширений алгоритм Евкліда.

5. Користувач B пересилає незахищеним каналом користувачу A пару чисел (N,  ).

Якщо користувач A має бажання передати користувачу B повідомлення М, він виконує такі кроки.

6. Користувач A розбиває вихідний відкритий текст М на блоки, кожний з яких може бути поданий у вигляді числа , .

7. Користувач A шифрує текст, поданий у вигляді послідовності чисел М, за формулою

і відправляє користувачеві В криптограму

.

6. Користувач B розшифровує прийняту криптограму , використовуючи таємний ключ , за формулою

.

У результаті буде отримана послідовність чисел , які являють собою вихідне повідомлення М. Щоб алгоритм RSA мав практичну цінність, необхідно мати можливість без істотних витрат генерувати великі прості числа, вміти оперативно обчислювати значення ключів та .

Наприклад, виконаємо шифрування повідомлення “Буду завтра”.

Нехай P=59, Q=61. Тоді , а . Виберемо як відкритий ключ довільне число з урахуванням виконання умов (4.6) і (4.7). Нехай . Згідно (4.8) таємний ключ .

Подамо повідомлення як послідовність цілих чисел у діапазоні від 1 до 32. Нехай A – 01, Б – 02, В – 03, ..., Я – 32.

Тоді повідомлення “Буду завтра” буде подано у вигляді

02 20 05 20 08 01 03 19 17 01.

Розбиваємо повідомлення на блоки по чотири цифри

0220 0520 0801 0319 1701

і кодуємо кожен блок:

У результаті одержимо шифр 0099 3273 2050 0719 1664.

Для відновлення вихідного тексту необхідно обчислити модульну експоненту, підвівши зашифроване значення в степінь за модулем N:

Таким чином, отримали відновлене вихідне повідомлення

0220 0520 0801 0319 1701.

Криптосистеми RSA реалізуються як апаратним, так і програмним шляхом.

Для апаратної реалізації операцій зашифрування та розшифрування RSA розроблені спеціальні процесори. Ці процесори, реалізовані на надвеликих інтегральних схемах, дозволяють виконувати операції RSA, пов’язані з піднесенням великих чисел у колосально великий ступінь за модулем N, за відносно короткий час.

Слід відзначити, що і апаратна, і програмна реалізації алгоритму RSA в декілька сот разів повільніші від реалізацій симетричних криптосистем. Мала швидкодія криптосистеми RSA обмежує сферу її застосування, але не перекреслює її цінність.

Безпека й швидкодія криптосистеми RSA

Безпека алгоритму RSA базується на труднощах розв’язання задачі факторизації великих чисел, що є добутками двох великих простих чисел. Дійсно, крипостійкість алгоритму RSA визначається тим, що після формування таємного ключа й відкритого ключа "стираються" значення простих чисел P й Q, і тоді винятково важко визначити таємний ключ за відкритим ключем , оскільки для цього необхідно розв’язати задачу знаходження дільників P та Q модуля N.

Розкладання величини N на прості множники Р і Q дозволяє обчислити функцію , а потім визначити таємне значення , використовуючи рівняння (4.8).

Іншим можливим способом криптоаналізу алгоритму RSA є безпосереднє обчислення або підбір значення функції . Якщо встановлено значення , то співмножники P й Q обчислюються досить просто. Справді, нехай

Знаючи (N), можна визначити х і потім y; знаючи х та y, можна визначити числа P і Q з таких співвідношень:

.

Однак ця атака не простіша задачі факторизації модуля N.

Задача факторизації є задачею, яка важко розв’язується для великих значень модуля N.

Спочатку автори алгоритму RSA пропонували для обчислення модуля N вибирати прості числа P й Q випадковим чином, по 50 десяткових розрядів кожне. Вважалося, що такі великі числа N дуже важко розкласти на прості множники. Один з авторів алгоритму RSA, Р.Райвест, вважав, що розкладання на прості множники числа з майже 130 десяткових цифр, наведеного в їхній публікації, зажадає більше 40 квадрильйонів років машинного часу. Однак цей прогноз не виправдався через порівняно швидкий прогрес обчислювальної потужності комп’ютерів, а також поліпшення алгоритмів факторизації.

Один з найбільш швидких алгоритмів, відомих у цей час, алгоритм NFS (Number Field Sieve) може виконати факторизацію великого числа N (із числом десяткових розрядів більше 120) за число кроків, оцінюваних величиною

У 1994 р. було факторизовано число з 129 десятковими цифрами. Це вдалося здійснити математикам А.Ленстра й М.Манассі за допомогою організації розподілених обчислень на 1600 комп’ютерах, об’єднаних мережею, протягом восьми місяців. На думку А.Ленстра та М.Манассі, їхня робота компрометує криптосистеми RSA і створює більшу погрозу їхнім подальшим застосуванням. Тепер розроблювачам криптоалгоритмів з відкритим ключем на базі RSA доводиться уникати застосування чисел довжиною менше 200 десяткових розрядів. Останні публікації пропонують застосовувати для цього числа довжиною не менше 300 десяткових розрядів.

4.4 Схема шифрування Поліга - Хеллмана

Схема шифрування Поліга - Хеллмана подібна RSA. Розглянута схема не є симетричним алгоритмом, оскільки використовуються різні ключі для шифрування та розшифрування. З іншого боку її не можна віднести й до класу криптосистем з відкритим ключем, тому що ключі шифрування та розшифрування легко виходять один з одного. Обидва ключі (відкритий і таємний) необхідно тримати в таємниці.

Аналогічно схемі RSA криптограма C і відкритий текст M визначаються зі співвідношень:

_, (4.14)

_, (4.15)

де

. (4.16)

На відміну від алгоритму RSA у цій схемі число N не визначається через два великих простих числа; число N повинне залишатися частиною таємного ключа. Якщо хто-небудь довідається значення та N, він зможе обчислити значення .

Не знаючи значень або , зловмисник буде змушений обчислювати значення

.

Відомо, що це є важкою задачею. Схема шифрування Поліга - Хеллмана запатентована в США [9] і Канаді.

4.5 Алгоритм шифрування Ель Гамаля

Алгоритм Ель Гамаля, розроблено в 1985 р., може бути використаний як для шифрування, так і для цифрових підписів. Безпека схеми Ель Гамаля обумовлена складністю обчислення дискретних логарифмів у кінцевому полі.

Для того щоб генерувати пари ключів (відкритий ключ і таємний ключ ), спочатку вибирають деяке велике просте число P і велике ціле число G степені якого за модулем P породжують велику кількість елементів множини , причому . Числа P й G можуть бути поширені серед групи користувачів.

Потім вибирають випадкове ціле число , причому . Число є таємним ключем і повинне зберігатися в секреті.

Далі обчислюють відкритий ключ

. (4.17)

Для того, щоб зашифрувати повідомлення М, вибирають випадкове ціле число , що задовольняє такі умови:

, (4.18)

. (4.19)

Потім обчислюють числа

(4.20)

(4.21)

Пари чисел (а,b) є шифротекстом. Помітимо, що довжина шифротексту вдвічі більша довжини вихідного відкритого тексту М.

Для того щоб розшифрувати шифротекст (а,b), обчислюють

. (4.22)

Довести, що співвідношення (4.22) справедливо, можна виходячи з (3.17) , (3.20) і (3.21), оскільки

.

Наприклад, виберемо Р = 17, G = 5, таємний ключ = 2. Обчислюємо

.

Отже, відкритий ключ = 8.

Нехай повідомлення М = {Д}={5}.

Виберемо деяке випадкове число K = 3. Перевіримо умову (3.19) дійсно НСД (3,16) =1. Обчислюємо пари чисел а та b:

Таким чином, шифротекстом для літери Д є пара чисел (6,10).

Виконаємо розшифрування цього шифротексту. Обчислюємо повідомлення М, використовуючи таємний ключ

.

Вираз

можна подати у вигляді

.

Розв’язуючи дане порівняння, знаходимо М = 5.

У реальних схемах шифрування необхідно використовувати як модуль P велике ціле просте число, що має у двійковому поданні довжину від 512 до 1024 бітів.

У системі Ель Гамаля відкритого шифрування той самий ступінь захисту, що для алгоритму RSA з модулем N з 200 знаків, досягається вже при модулі P в 150 знаків. Це дозволяє в 5-7 разів збільшити швидкість обробки інформації. Але у такому варіанті відкритого шифрування немає підтвердження достеменності повідомлень.

Система Ель Гамаля не позбавлена певних недоліків. Серед них можна зазначити такі:

1 Відсутність семантичної стійкості. Якщо G – примітивний елемент множини , то за поліноміальний час можна визначити чи є деяке число x квадратичним відрахуванням. Це робиться піднесенням числа x у степінь за модулем P

.

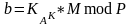Якщо результат дорівнює 1, то х – квадратичне відрахування за модулем Р, якщо –1 , то х – квадратичне невирахування. Далі пасивний зловмисник перевіряє, чи є G^K і квадратичними відрахуваннями. буде квадратичним відрахуванням тоді й тільки тоді, коли і G^K , і будуть квадратичними відрахуваннями. Якщо це так, то буде квадратичним відрахуванням тоді й тільки тоді, коли саме повідомлення М буде квадратичним відрахуванням. Тобто пасивний зловмисник одержує деяку інформацію про вихідний текст, маючи лише шифрований текст і відкритий ключ одержувача.

2 Подільність шифру. Якщо дано шифрований текст (a, b), можна одержати інший шифрований текст, змінивши тільки другу частину повідомлення. Справді, помноживши b на G^U (U0), можна одержати шифротекст для іншого вихідного повідомлення .

4.6 Схема шифрування Рабіна

Схема Рабіна була розроблена в 1979 році й може застосовуватися тільки для шифрування даних. Безпека алгоритму спирається на складність пошуку коренів за модулем складеного числа.

Для генерації ключів вибирається пара простих чисел , таких що

(4.23)

Ці прості числа і є таємним ключем. Відкритим ключем є число

. (4.24)

Для шифрування повідомлення , де , обчислюється

. (4.25)

Для розшифрування повідомлення за допомогою китайської теореми про залишки обчислюється:

(4.26)

Потім вибираються два цілих числа

(4.27)

Чотирма можливими рішеннями є:

(4.28)

Одне із чотирьох результатів, і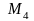 , є повідомлення .

Наприклад, виконаємо шифрування тексту , використовуючи схему шифрування Рабіна. Згідно з (4.23) виберемо пари чисел , нехай й . Тоді, відкритий ключ N=77.

Шифротекст C згідно з (4.25)

.

Виконаємо розшифрування. Виходячи з (4.26), маємо

Згідно з (4.27)

Тоді за (4.28) одержимо

Дійсно, одне із чотирьох значень, а саме: і є відкритий текст .

5 Керування ключами

При симетричному шифруванні обидві сторони, що беруть участь в обміні даними, повинні одержати однакові ключі, до яких сторонні учасники позбавлені доступу. Одночасно із цим необхідна часта зміна ключів, щоб зменшити обсяг даних, що втрачаються через розкриття ключа зловмисником. Тому надійність будь-якої криптосистеми залежить від системи розподілу ключів, що використовується. Система розподілу ключів являє собою систему доставки ключів сторонам, що планують обмін даними, і не дозволяє іншим сторонам скористатися цими ключами.

Розподіл ключів можна організувати різними способами.

1. Ключ може бути обраний однією стороною та фізично доставлений іншій стороні, що бере участь у процесі обміну даними.

2. Ключ може вибрати третя сторона та фізично доставити його учасникам обміну.

3. Якщо сторони, які беруть участь в обміні, вже використовують який-небудь ключ, то одна із сторін може передати іншій стороні новий ключ, зашифрований з використанням старого.

4. Якщо обидві сторони обміну мають криптографічно захищені канали і зв'язки із третьою стороною, то остання може доставити ключ учасникам обміну по цих захищених каналах.

5. Ключ може бути генерований обома учасниками обміну з використанням алгоритму генерації.

Схеми 1 та 2 припускають передачу ключів з рук у руки. Цей спосіб прийнятний при канальному шифруванні, але у випадку наскрізного шифрування фізична доставка ключа є практично неприйнятною.

Схему 3 можна застосувати як для канального, так і для наскрізного шифрування, але якщо зловмисникові стане коли-небудь відомо значення одного із ключів, то йому стануть відомі і всі наступні ключі.

Варіант схеми 4 часто застосовується при наскрізному шифруванні. Так за доставку ключів учасникам обміну відповідає якийсь центр розподілу ключів (ЦРК). При цьому кожен користувач одержує свій унікальний ключ, використовуваний ним разом із ЦРК для організації доставки ключів.

Використання ЦРК припускає організацію ієрархії ключів. Зв'язок між ЦРК і учасником майбутнього обміну шифрується з використанням сеансового ключа. Як правило, сеансовий ключ використовують для конкретного логічного з'єднання і надалі більше не застосовують. Сеансовий ключ одержують від центра тими самими каналам, які використовуються для організації зв'язку між кінцевими користувачами – учасниками майбутнього обміну даними. Відповідно сеансові ключі передаються в зашифрованому вигляді, а для шифрування використовують головний ключ, спільний для ЦРК і кінцевого користувача.

Прикладом реалізації схеми 5 може бути алгоритм генерації ключів Діффі-Хеллмана.

5.1 Алгоритм шифрування Діффі - Хеллмана

Алгоритм Діффі-Хеллмана допомагає обмінюватися секретним ключем для симетричних криптосистем з використанням каналу, захищеного від модифікації, тобто дані, передані цим каналом, можуть бути прослухані, але не змінені. У цьому випадку дві сторони можуть створити однаковий секретний ключ, жодного разу не передавши його по мережі, згідно з таким алгоритмом.

Припустимо, що обом учасникам обміну відомі деякі два натуральні числа M і N, де N – просте число . Вони можуть бути відомі й усім іншим зацікавленим особам. Для того щоб створити невідомий більше нікому секретний ключ, обидві сторони генерують випадкові числа: перший абонент – число X, другий абонент – число Y.

Потім перший абонент обчислює значення

і пересилає його другому учаснику, а другий учасник обчислює значення

і передає його першому.

Зловмисник одержує обидва значення та , але модифікувати їх (втрутитися в процес передачі) не може.

На другому етапі перший абонент, на основі наявного в нього числа X й отриманого по мережі числа , обчислює значення

,

а другий абонент на основі наявних у нього чисел Y та обчислює значення

.

Неважко переконатися, що в обох учасників вийшло те саме число  :

Числа можуть використовуватися як ключі при обміні даними з використанням традиційних систем шифрування.

Наприклад, нехай абонентам і відомі деякі два числа M =17 й N=23.

Абонент генерує випадкове число Х=3 й обчислює значення

L_A=11³ mod 23=14.

Абонент генерує випадкове число Y=5 й обчислює значення

L_B=17⁵ mod 2321.

Абонент передає абонентові значення L_A,, а абонент абонентові значення L_В. Кожний з абонентів та обчислюють секретний ключ згідно з прийнятими даними L_A і L_В.

А: ,

B: .

При спробі визначити значення чисел X та Y за перехопленим значенням і супротивник зіштовхнеться із задачею дискретного логарифмування, що є важко розв'язною.

Ще раз відзначимо, що алгоритм Діффі-Хеллмана працює тільки на лініях зв'язку, надійно захищених від модифікації.