Введемо деякі поняття, необхідні в подальшому розгляді курсу криптології:

Алфавіт – кінцева множина використовуваних для шифрування інформації знаків.

Текст – упорядкований набір з елементів алфавіту.

Шифр або криптографічний алгоритм – сукупність оборотних перетворень множини відкритих даних на множину зашифрованих даних, заданих алгоритмом криптографічного перетворення. Інакше кажучи, криптоалгоритм – це математична функція, що використовується для шифрування та розшифрування інформації.

Зашифрування – перетворення відкритих даних у закриті (зашифровані) за допомогою певних правил, які визначені в шифрі.

Розшифрування – процес, зворотний зашифруванню.

Розкриття (зламування) шифру – процес перетворення закритих даних у відкриті при невідомому ключі й (або) невідомому алгоритмі.

Ключ – це змінний елемент шифру, який застосовують для закриття окремого повідомлення. Інакше кажучи, ключ – це конкретний секретний стан параметрів криптоалгоритма, що забезпечує вибір одного варіанта перетворення із сукупності можливих.

Саме ключем визначається в першу чергу безпека інформації, що шифрується, і саме тому перетворення, які застосовуються в надійних шифрах, залежать від ключа. А функції зашифрування та розшифрування мають такий вигляд:

E_K(M)=C, (2.1)

D_K(M)=M, (2.2)

де

М – відкритий текст повідомлення;

Е_К – процес зашифрування із ключем K.

D_К – процес розшифрування із ключем К.

При цьому справедлива така рівність

D_K(E_K(M))=М; (2.3)

Рівності 2.1 – 2.3 справедливі для симетричних криптосистем або криптосистем із закритим ключем. Ці алгоритми вимагають, щоб перед початком передачі таємних повідомлень учасники обміну погодили, який ключ буде використаний.

Захист інформації в даних криптосистемах забезпечується таємністю ключа. Це означає, що як тільки ключ буде розкритий, секретною інформацією може скористатися будь-хто. Процес зашифрування та розшифрування в симетричних криптосистемах виглядає так, як показано на рис 2.1.

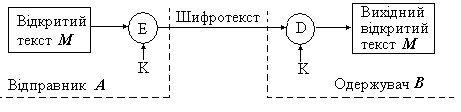
Рисунок 2.1 – Симетричні криптосистеми

В асиметричних криптосистемах для шифрування та розшифрування використовуються різні ключі. Для асиметричних криптосистем справедливі рівності 2.4-2.6:

(2.4)

(2.5)

При цьому справедлива така рівність:

, (2.6)

де

– ключ шифрування;

– ключ розшифрування.

Процес зашифрування та розшифрування в асиметричних криптосистемах виглядає так, як показано на рис 2.2

Рисунок 2.2 – Асиметричні криптосистеми

Шифрування – процес зашифрування або розшифрування.

Криптосистема складається із простору ключів, простору відкритих текстів, простору шифротекстів та алгоритмів зашифрування і розшифрування.

Розкриття криптоалгоритма – результат роботи криптоаналітика, що приводить до можливості ефективного визначення будь-якого зашифрованого за допомогою даного алгоритму відкритого тексту.

Стійкість криптоалгоритма – здатність шифру протистояти всіляким спробам його розкриття, тобто атакам на нього.

Усі сучасні шифри базуються на принципі Кірхгофа, відповідно до якого таємність шифру забезпечується таємністю ключа, а не таємністю алгоритму шифрування.

Якщо захист інформації, що забезпечується алгоритмом, засновано на таємності самого алгоритму, то криптоалгоритм називають обмеженим. Такі алгоритми мають масу недоліків, так, наприклад, алгоритм повинен бути замінений:

• при виході користувача із групи, якщо група використає такий алгоритм;

• якщо сторонній випадково довідається секрет групи.

Групи, що використовують обмежені алгоритми, не можуть використовувати відкриті апаратні або програмні продукти, оскільки зловмисник може придбати такий продукт і розкрити секрет. Крім того, такі алгоритми погано піддаються стандартизації та контролю, вони звичайно не проходять оцінки надійності й т.д. Але, незважаючи на це, такі алгоритми дуже популярні в програмних додатках з низьким рівнем захисту.

Тому аналіз надійності таких систем завжди повинен проводитися виходячи з того, що супротивник має всю інформацію про криптоалгоритм, який був застосований, і для нього невідомо тільки значення реально використаного ключа. У зв’язку з вищевикладеним можна сформулювати загальне правило: при створенні або при аналізі стійкості криптосистем не слід недооцінювати можливості супротивника.

До найбільш часто використовуваних на практиці методів оцінки якості криптоалгоритмів можна віднести:

• будь-які спроби розкриття криптоалгоритмів. Тут багато чого залежить від кваліфікації, досвіду, інтуїції криптоаналітика і від правильної оцінки можливостей супротивника;

• аналіз складності алгоритму дешифрування. Складність обчислювальних алгоритмів можна оцінювати числом виконуваних елементарних операцій при цьому природно, необхідно враховувати їхню вартість і витрати на їхнє виконання. Якісний шифр неможливо розкрити способом більш ефективним, ніж повний перебір по всьому ключовому простору. При цьому криптограф повинен розраховувати тільки на те, що в супротивника не вистачить ні часу, ні ресурсів, щоб це зробити;

• оцінка статистичної безпеки шифру. Надійна криптосистема з погляду супротивника є "чорним ящиком", вхідна та вихідна інформаційні послідовності якого взаємно незалежні, при цьому вихідна зашифрована послідовність є псевдовипадковою. Тому зміст випробувань полягає в проведенні статистичних тестів, що встановлюють залежність змін у зашифрованому тексті від змін символів або бітів у вихідному тексті, або ключі, а також аналізують, наскільки вихідна зашифрована послідовність за своїми статистичними властивостями наближається до істинно випадкової послідовності.

Відзначимо необхідні умови стійкості будь-якої криптосистеми, що перевіряють статистичними методами:

• відсутність статистичної залежності між вхідною та вихідною послідовностями;

• вихідна послідовність за своїми статистичними властивостями повинна бути схожа на істинно випадкову послідовність;

• при незмінній вхідній інформаційній послідовності незначна зміна ключа повинна приводити до істотної зміни вихідної послідовності;

• при незмінному ключі незначна зміна вхідної послідовності повинна приводити до істотної зміни вихідної послідовності;

• відсутність залежності між ключами, які послідовно використовуються в процесі шифрування.

Існує багато різних криптоалгоритмів, при цьому немає жодного, підходящого для всіх випадків. У кожній конкретній ситуації вибір криптоалгоритму визначається такими факторами:

• особливістю інформації, що захищається (документи, вихідні тексти програм, графічні файли і т. ін.);

• особливістю середовища зберігання і передачі інформації;

• цінністю інформації, характером секретів, що захищають, часом забезпечення таємності;

• обсягами інформації, швидкістю її передачі, ступенем оперативності її надання користувачеві;

• можливостями власників інформації, власників засобів збору, обробки, зберігання та передачі інформації з її захисту;

• характером погроз, можливостями супротивника.

Алгоритм Евкліда

Досить простою процедурою пошуку НСД є алгоритм Евкліда.

Нехай дані два числа a, bZ, причому 0<b<a. Необхідно визначити НСД. Для цього ділять a на b. Якщо b a, то найбільшим спільним дільником є число b. Якщо a не ділиться на b націло, то одержують частку та залишок , причому 0 <b. Далі ділять b на , одержують частку і залишок , причому 0 < . Далі аналогічно ділять на , при цьому одержують частку і залишок , причому 0 < . І так далі. Цей процес закінчується в тому випадку, коли залишок від ділення буде дорівнювати нулю, тобто процес ділення є кінцевим, оскільки залишки , , ,…, будучи натуральними числами, зменшуються. Останній залишок, що не дорівнює нулю, є найбільшим спільним дільником чисел a та b.

Алгоритм Евкліда можна сформулювати у вигляді теореми.

Теорема 3 Якщо

,

то НСД(a, b)= .

Наприклад, щоб знайти НСД (2585, 7975) виконаємо такі дії:

7975=25853+220, ,

2585=22011+165, ,

220=1651+55, ,

165=553.

Відповідно до теореми 3 НСД(2585, 7975) =55.

В алгоритмі Евкліда розгляд можна обмежити тільки додатними числами, тому що НСД(a,b)=НСД(|a|, |b|).

procedure Euclid (a,b: integer; var nsd);

var r:integer;

begin

a:=abs(a);

b:=abs(b);

r:=a mod b;

if r=0

then

nsd:=b;

else

while r<>0 do

begin

a:=b;

b:=r;

nsd:=r;

r:=a mod b;

end;

end;

Для знаходження НСД декількох чисел спочатку знаходять

,

потім

,

…,

.

У результаті одержимо .

Теорема 4 Якщо , то існують такі числа x, yZ, що

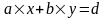. (1.1)

Рівність (1.1) називають лінійним поданням найбільшого спільного дільника чисел a та b.

1.3 Взаємно прості числа

Визначення. Якщо НСД(a,b)=1, то такі числа називаються взаємно простими числами.

Наприклад, числа 21 і 25 є взаємно простими числами, оскільки НСД(21, 25)=1.

Визначення. Якщо НСД( )=1, то такі числа називаються попарно взаємно простими числами або взаємно простими.

Розглянемо кілька властивостей взаємно простих чисел.

Для a, b, cZ:

1. Якщо два числа a та b взаємно прості, та , то числа та – взаємно прості.

2. Частки від ділення чисел a та b на їх найбільший спільний дільник d – взаємно прості

НСД .

3. Якщо і НСД , то .

4. Якщо НСД(a, b)=1, то число тоді й тільки тоді, коли b с и a с.

5. Якщо НСД(a, c)=1 і НСД(b, c)=1, то НСД( , c)=1.

1.4 Прості числа

Розглянемо цілі додатні числа.

Число 1 має тільки один дільник, а саме 1. Кожне натуральне число a, відмінне від 1, має принаймні два дільники – 1 і саме число a.

Визначення. Відмінне від одиниці натуральне число a називається простим, якщо його дільниками є 1 і саме число a. Число a називається складеним, якщо воно має дільники, відмінні від 1 і самого числа a.

Слід зазначити, що число 1 не належить ні до простих, ні до складених чисел.

Розглянемо деякі властивості простих і складених чисел:

1. Будь-яке натуральне число або ділиться на дане просте число, або взаємно просте з ним .

2. Якщо добуток декількох натуральних чисел ділиться на просте число p, то принаймні один із співмножників ділиться на це просте число p.

3. Найменший дільник p ( ) натурального числа n є число просте.

4. Найменший відмінний від 1 дільник складеного числа a не більший ніж .

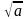Теорема 5 Кожне відмінне від 1 натуральне число єдиним способом розкладається на прості множники.

Може виявитися, що в розкладанні числа aN на прості множники будуть однакові числа, тому якщо скористатися поняттям ступеня, то число можна записати так:

, (1.2)

де – прості числа, і кожне >0 (i=1, 2,…, s)...

Рівність (1.2) називається канонічною формою розкладання натурального числа a.