
- •Инерциальные системы отсчета. Понятия силы и инертной массы. Законы динамики. Силы в природе. Фундаментальные взаимодействия. Свойства сил упругости и тяготения. Свойства сил трения.
- •Колебания математического и физического маятников.
- •Преобразования Галилея. Механический принцип относительности. Нарушение классического закона сложения скоростей. Опыты по определению скорости света. Опыт Майкельсона.
- •Среднеквадратичная скорость молекул. Молекулярно-кинетическое толкование абсолютной температуры.
- •Основное уравнение молекулярно-кинетической теории (вывод). Число степеней свободы молекулы. Закон распределения энергии по степеням свободы. Внутренняя энергия идеального газа.
- •Изопроцессы идеального газа. Зависимость теплоемкости от вида процесса. Адиабатический процесс.
- •Тепловые двигатели и холодильные машины. Кпд. Обратимые и необратимые процесы. Круговой процесс. Цикл Карно для идеального газа и его кпд
- •Принцип работы цикла Карно.
- •Закон Максвелла для распределения молекул идеального газа по скоростям теплового движения. Вероятностное толкование закона распределения Максвелла
- •Явления переноса. Теплопроводность, диффузия, вязкость.
- •Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Уравнение Ван-дер-Ваальса. Изотермы реального газа. Критическое состояние. (Внутренняя энергия реального газа.)
Принцип работы цикла Карно.
Рабочее
вещество температурой T1
и объёмом V1
изотермически расширяется до объёма
V2, получая
количество тепла Q1
от горячего источника. При этом газ
производит работу
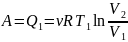 .
Затем газ адиабатно расширяют до объёма
V3, отчего
его температура падает до T2.
Далее рабочее вещество изотермически
сжимается до объёма V4,
при этом газ отдаёт холодному источнику
количество теплоты
.
Затем газ адиабатно расширяют до объёма
V3, отчего
его температура падает до T2.
Далее рабочее вещество изотермически
сжимается до объёма V4,
при этом газ отдаёт холодному источнику
количество теплоты
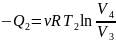 ,
откуда
,
откуда
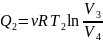 .
Тогда КПД равно:
.
Тогда КПД равно:
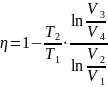 .
Отсюда видно, что КПД не зависит от
количества рабочего вещества.
.
Отсюда видно, что КПД не зависит от
количества рабочего вещества.
Запишем уравнение адиабаты идеального газа для двух адиабатных процессов:
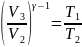
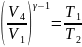
Откуда
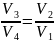 .
.
Подставив
эту формулу в выражение КПД цикла,
получим:
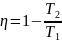 .
.
Таким
образом, КПД цикла Карно, произведенного
с идеальным газом, определяется только
температурами горячего и холодного
источников тепла. При этом КПД тем
больше, чем больше разность между
температурами источников. КПД цикла
Карно равен 1 в двух практически
недостижимых случаях: когда
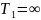 или когда
или когда
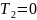 .
Если КПД цикла равен единице, то
.
Если КПД цикла равен единице, то
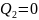 ,
т. е. все тепло Q1 , полученное
от горячего источника, преобразуется
в работу, что запрещено вторым началом
термодинамики. Следовательно, КПД
никакого цикла, в том числе и цикла
Карно, не может быть равен единице.
,
т. е. все тепло Q1 , полученное
от горячего источника, преобразуется
в работу, что запрещено вторым началом
термодинамики. Следовательно, КПД
никакого цикла, в том числе и цикла
Карно, не может быть равен единице.
Второе начало термодинамики. Вечный двигатель второго рода. Статистическое толкование второго начала термодинамики. Энтропия в термодинамике. Изменение энтропии при изопроцессах. Статистическое толкование энтропии
Второе начало термодинамики утверждает, что самопроизвольный переход тепла от менее нагретого тела к более нагретому невозможен.
Вечный двигатель второго рода - это машина, которая превращает всё тепло, извлекаемое из окружающих тел, в работу. Такой двигатель невозможен, потому что его существование нарушало бы второй закон термодинамики.
Статистическое толкование второго начала термодинамики: самопроизвольный переход из неравновесного состояния в равновесное является гораздо более вероятным, чем обратный переход.
Энтропия - это функция состояния термодинамической системы.
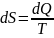 .
.
Закон
неубывания энтропии в замкнутых системах:
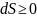 .
.
Энтропия при изобарном процессе: .
Энтропия при изохорном процессе: .
Энтропия при изотермическом процессе: , где dS - приращение энтропии в системе, а δQ - бесконечно малое количество теплоты, полученное этой системой.
Статистическое толкование энтропии: энтропия является мерой неупорядоченности системы.
Термодинамическая вероятность - число способов, которыми может быть реализовано состояние физической системы.
Энтропия
системы и термодинамическая вероятность
связаны между собой следующим образом:
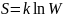 ,
где k - постоянная
Больцмана.
,
где k - постоянная
Больцмана.
Закон Максвелла для распределения молекул идеального газа по скоростям теплового движения. Вероятностное толкование закона распределения Максвелла
Джеймс Максвелл нашел вид функции распределения молекул идеального газа по модулям скоростей хаотического движения.
Если газ находится в равновесии, молекулы движутся хаотически, и все направления их движения равновероятны. Скорости молекул могут быть самыми различными по модулю и при каждом соударении с другими молекулами изменяются случайным образом.
В газе, находящемся в состоянии равновесия, устанавливается стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был выведен теоретически Джеймсом Максвеллом. Максвелл предполагал, что вещество состоит из очень большого числа тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют.
(Вероятностное толкование закона распределения Максвелла - без понятия.)
Барометрическая формула. Закон Больцмана для распределения частиц идеального газа во внешнем потенциальном поле.
Барометрическая
формула определяет зависимость
давления от высоты в поле силы тяжести:
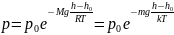 ,
где T - абсолютная
температура газа, h -
высота слоя газа, p0
- давление на нулевом уровне h0,
M - молярная масса
газа.
,
где T - абсолютная
температура газа, h -
высота слоя газа, p0
- давление на нулевом уровне h0,
M - молярная масса
газа.
Распределение
Больцмана - это распределение по
энергиям частиц (атомов, молекул)
идеального газа в условиях термодинамического
равновесия:
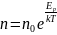 ,
где n - число молекул
в единичном объёме на высоте h,
n0 - число
молекул в единичном объёме на высоте
h0=0.
,
где n - число молекул
в единичном объёме на высоте h,
n0 - число
молекул в единичном объёме на высоте
h0=0.
Среднее число столкновений и средняя длина свободного пробега молекул идеального газа. Эффективный диаметр молекулы.
Длина свободного пробега молекулы - расстояние, которое проходит молекула между двумя соударениями с другими молекулами. Средняя длина свободного пробега молекулы - это средняя длина свободного пробега среди всех молекул газа.
Число столкновений молекулы - количество столкновений молекулы с другими за промежуток времени. Среднее число столкновений молекулы - среднее количество столкновений с другими молекулами среди всех молекул.
Эффективный диаметр молекулы - минимальное расстояние, на которое сближаются молекулы при соударении. Он зависит от скорости движения молекул (т.е. от температуры газа).
Так как
за 1 с молекула в среднем проходит путь,
который равен средней арифметической
скорости v, и если z
- среднее число столкновений, которые
одна молекула газа делает за 1 с, то
средняя длина свободного пробега будет
равна:
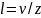 .
.
Среднее
число столкновений
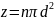 .
.
