2 7. Линии наибольшего наклона (ската)

Линией наибольшего ската плоскости γ называется прямая g, принадлежащая этой плоскости и перпендикулярная ее линиям уровня: горизонтали h и фронтали f.

На комплексном чертеже горизонтальная проекция линии наибольшего наклона перпендикулярна горизонтальной проекции горизонтали этой плоскости, а фронтальная − фронтальной проекции фронтали. Главным свойством этой линии наибольшего ската является то, что она образует с горизонтальной плоскостью проекций π₁ угол α°, равный углу наклона плоскости γ к плоскости π₁. Это свойство линии наибольшего наклона (ската) используется для определения углов наклона плоскостей к плоскостям проекций.

Зададим плоскость Ф треугольником АВС (рис. 2-21).

Алгоритм решения задачи:

1. Проводим в плоскости Ф(АВС) горизонталь h(h₁,h₂).

2. Проводим g₁(B₁K₁) ^ h1. Находим g₂(B₂K₂) по принадлежности плоскости.

3. Находим натуральную величину g методом прямоугольного треугольника (рис. 2-21).

4. Угол a между g₁ u g - есть угол наклона плоскости Ф(АВС) к П₁.

(Полное решение задачи)

Аналогично можно решить задачу на определение угла наклона плоскости Ф к П₂. Для этого в плоскости Ф нужно взять фронталь, линию наибольшего наклона плоскости к П₂ - е строить перпендикулярно фронтали (е₂^ f₂® е) и находить натуральную величину е на П₂.

После вышесказанного, рассмотрим задание плоскости с помощью линии ската g и линии наибольшего наклона плоскости к П₂ - е.

В первом случае при решении конкретных задач к линии ската необходимо добавить горизонталь (h₂^ линиям связи, h₁^ g₁); во втором к линии наибольшего наклона е добавляют фронталь (f₁^ линиям связи, f₂^ е₂). В обоих случаях плоскость получается заданной пересекающимися прямыми.

28. Метод сфер

С пособ концентрических сфе

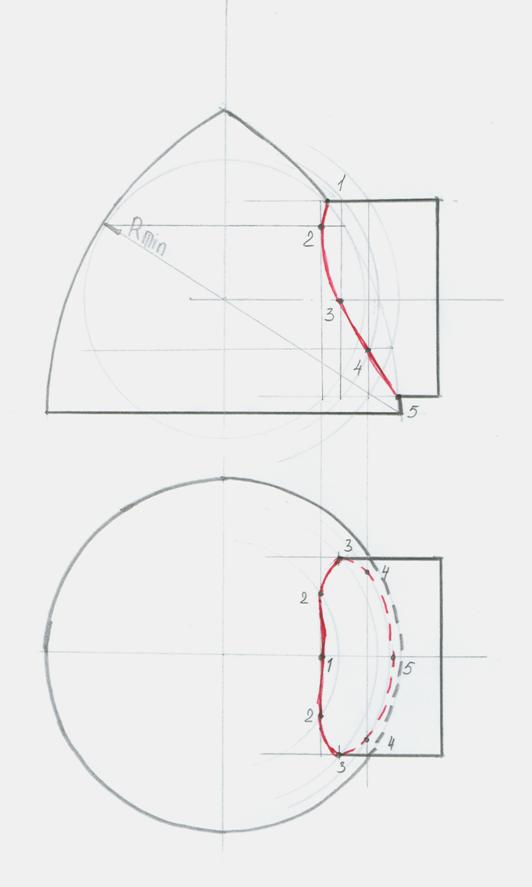
Этот метод применяется в том случае, если данные поверхности являются поверхностями вращения, оси вращения пересекаются и параллельные одной плоскости проекций. Методом сфер находят проекцию линии пересечения на той плоскости проекций, которой параллельны оси вращения исходных поверхностей. Видимая и невидимая части линии пересечения совпадают, а потому порядок проекции линии пересечения в два раза меньше порядка самой линии пересечения. Другую проекцию линии пересечения находят по принадлежности ее одной из исходных поверхностей. Ее порядок в общем случае равен порядку линии пересечения. Метод основан на свойстве соосных поверхностей вращения пресекаться по окружностям, которые проецируются в виде отрезков прямых линий.

Способ сфер можно применять при соблюдении условий:

1. Обе поверхности вращения.

2. Оси поверхностей пресекаться

3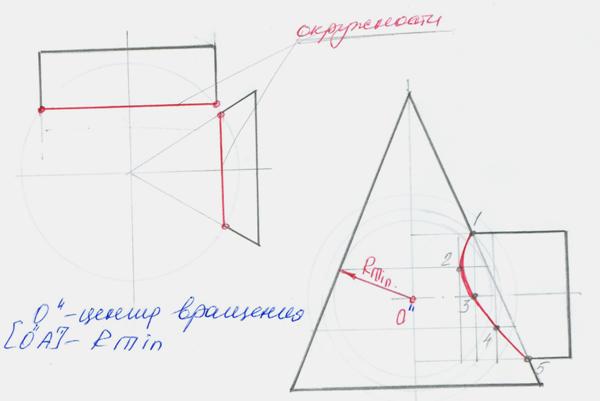 . Плоскость, которую образуют оси пересекающихся тел, параллельна одной из плоскостей проекций.

Минимальный радиус сферы должен быть касательным к большей поверхности.