Поверхности вращения, точки на поверхностях
Поверхностью вращения называют поверхность получаемую от вращения какой либо линии (образующей) вокруг неподвижной оси.
Образующая зафиксирована в том или ином положении называется меридианом.
Если пересекать поверхности вращения плоскостями перпендикулярными к оси вращения, получаются в сечении окружности. Такие окружности называются параллелями. Наибольшую из параллелей называют экватором, наименьшую горлом.
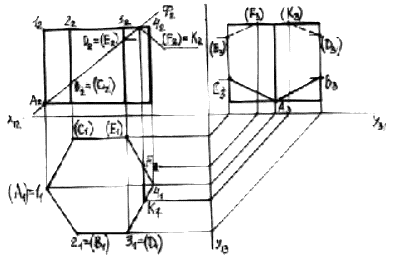
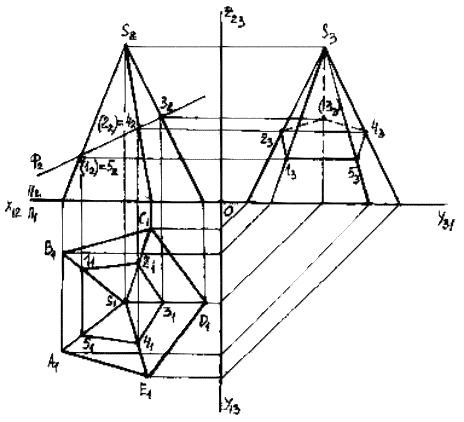
Сечение гранных поверхностей плоскостью частного положения
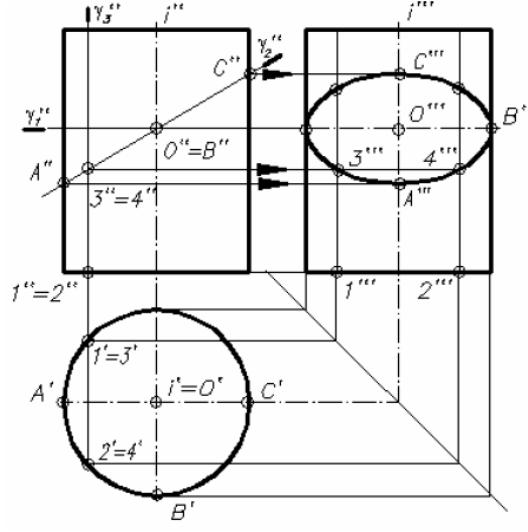
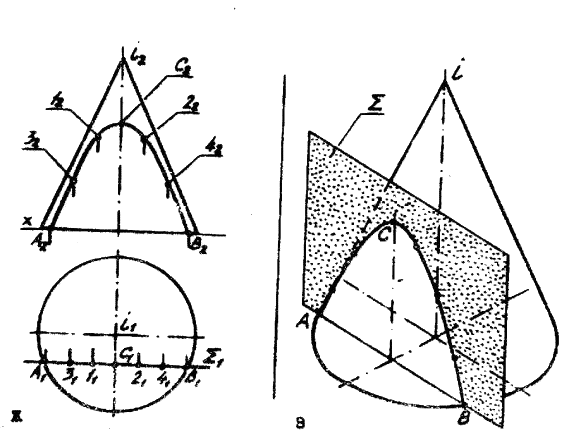
Сечение тел вращения плоскостью частного положения
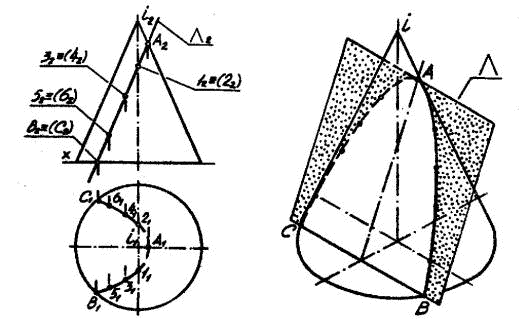
Пересечение прямой линии с поверхностью гранной
Пересечение линий с поверхностью
Алгоритм решения:
1
.
Через прямую провести плоскость
(проецирующая) .
2. Найти линию пересечения этой плоскости с поверхностью.
3. Точки пересечения заданной прямой с построенной линией и будут точками пересечения прямой с поверхностью.
