23. Радиоканалы

На распространение радиоволн влияют отражающие и поглощающие свойства слоя ионосферы, расположенного в верхней части атмосферы. Волны, распространяющиеся вследствие множественных переотражений в атмосфере, носят название пространственных. Кроме пространственных волн имеют место, т.н. поверхностные волны, распространяющиеся вблизи поверхности Земли, благодаря дифракции. Чем меньше длина волны, тем быстрее затухают поверхностные волны. УКВ сразу выходят за пределы атмосферы.

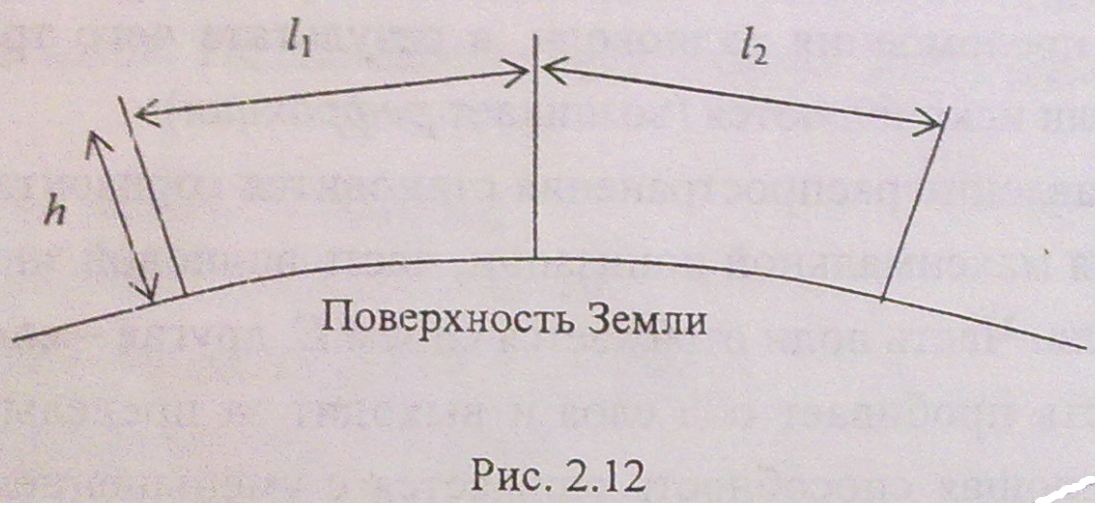
Для передачи информации на большие расстояния используются про­межуточные ретрансляторы, служащие и для частичного восстановления сигналов, искаженных и ослабленных в процессе передачи. Если прямая ви­димость ограничена только кривизной земной поверхности, то расстояние между станциями определяется по формуле: l (км)  7,2 .

24. Телерадиоканалы.

В радиотелевизионных каналах помимо аудиоинформации передается видеоинформация - так называемая картинка. Качество «картинки» определяется целым рядом причин, однако важнейшим звеном является так называемая передающая трубка, формирующая электронный видеосигнал из «оптического» изображения.

В многоканальных системах «тракты» всех сигналов должны отделять­ся друг от друга с тем, чтобы сигнал от каждого источника мог попасть на свой приемник.

Различают следующие способы разделения каналов: 1)пространственное разделение (это единственный вид, когда каждый канал получает свою линию). В остальных случаях линия является об­щей, а разделение получает характер уплотнения каналов; 2)дифференциальное; 3)частотное; 4)временное; 5)фазовое; 6)кодовое; 7)по уровням; 8)по форме; 9)корреляционные; 10)комбинированные методы и др.

25. Восприятие информации оператором. Формирование концептуальной модели.

26. Свойства сенсоров визуальной информации.

На эффективность зрительного восприятия оператором определенного объекта влияют, в основном следующие факторы :

1. Угловые размеры объекта;

2. Уровень адаптирующей яркости;

3. Контраст между объектом и фоном;

4. Время наблюдения объекта;

5. Цветоощущение.

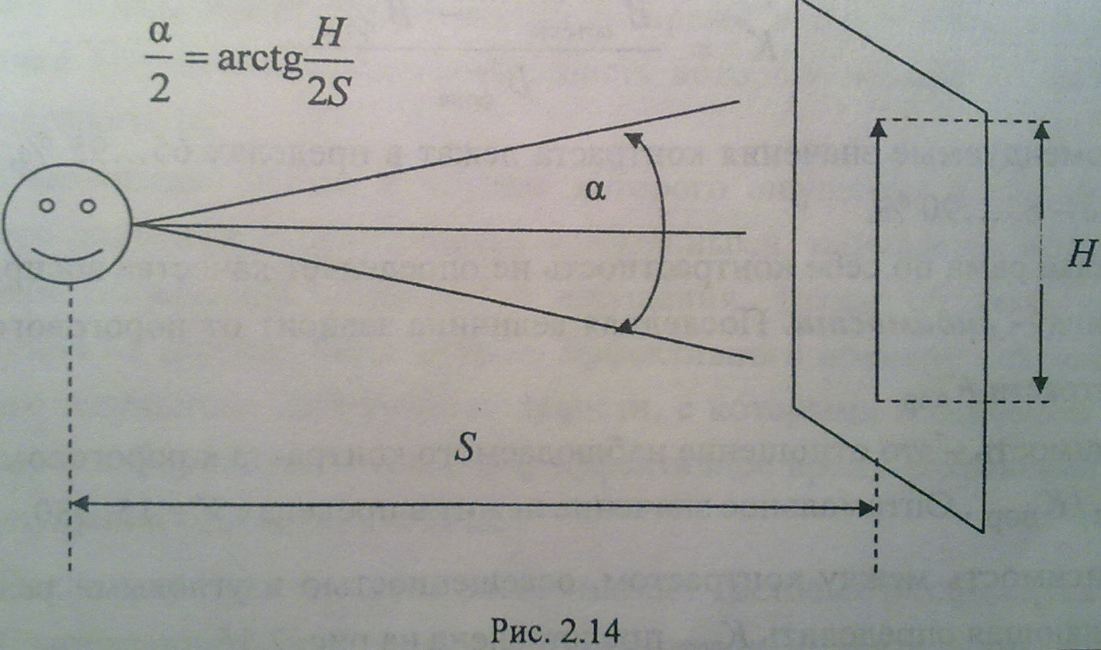
Под угловым размером объекта понимают угол между лучами, направленными от глаза наблюдателя к крайним точкам объекта

Адаптирующей яркостью называется яркость, на которую настроен (адаптирован) глаз оператора. При наблюдении сложных объектов она определяется как среднее суммы яркостей отдельных фрагментов изображения.

Наличие слепящих источников, так же как и недостаточная яркость вызывают быстрое зрительное, а, следовательно, и общее утомление оператора, а значит и возрастание времени формирования концептуальной модели.

В очень большой мере видимость объекта зависит от разницы в яркости между объектом и фоном. Отношение разности яркости объекта и фона к яркости фона называется яркостным контрастом. Различают два вида контраста: прямой и обратный. Уровень яркостного контраста есть: .

Однако сама по себе контрастность не определяет качества восприятия изображения - видимости. Последняя величина зависит от порогового значения контраста К_пор.

Видимость - есть отношение наблюдаемого контраста к пороговому:V = . Оптимальное значение лежит в пределах V = 15…30.

Восприятие предмета человеком сильно зависит от времени наблюде­ния объекта. Между моментами светового воздействия и возникновения зри­тельного ощущения проходит некоторое время, обозначаемое как время об­разования ощущения, продолжительность которого зависит от интенсивно­сти раздражителя.

Наименьшее время, в течение которого ощущения достигают макси­мального значения и сохраняются неизменными, называется эффективным временем сохранения зрительного ощущения. Таким образом, временная экспозиция не должна быть меньше эффективного времени сохранения зри­тельного ощущения.

При малой частоте вспышек каждая из них фиксируется отдельно. С ростом частоты появляются ощущения мерцания, а затем - слитного сигнала. Минимальная частота вспышек, обеспечивающая слитные восприятия, назы­вается критической частотой мельканий. Она зависит от яркости и угловых размеров объекта. Хорошим средством уменьшения времени восприятия сигналов является цветовое кодирование. «Колбочковый» аппарат сетчатки глаза че­ловека чувствителен к длине световых волн. Глаз в норме различает 7 основ­ных цветов спектра и до 180 их оттенков. Чувствительность (ощущение цве­та) глаза к различным участкам спектра неодинакова.

В видимой части спектра от 400 нм (фиолетовый) до 700 нм (красный) возникает необходимость оценивать излучение по способности вызывать психофизиологические ощущения.

На рис. 2.17 показана функция относительной спектральной чувстви­тельности К_λ глаза, адаптированного на дневное 1 и ночное 2 освещение. В области максимума (555 нм), где К_λ =1, коэффициент перевода составляет 680 лм/Вт.

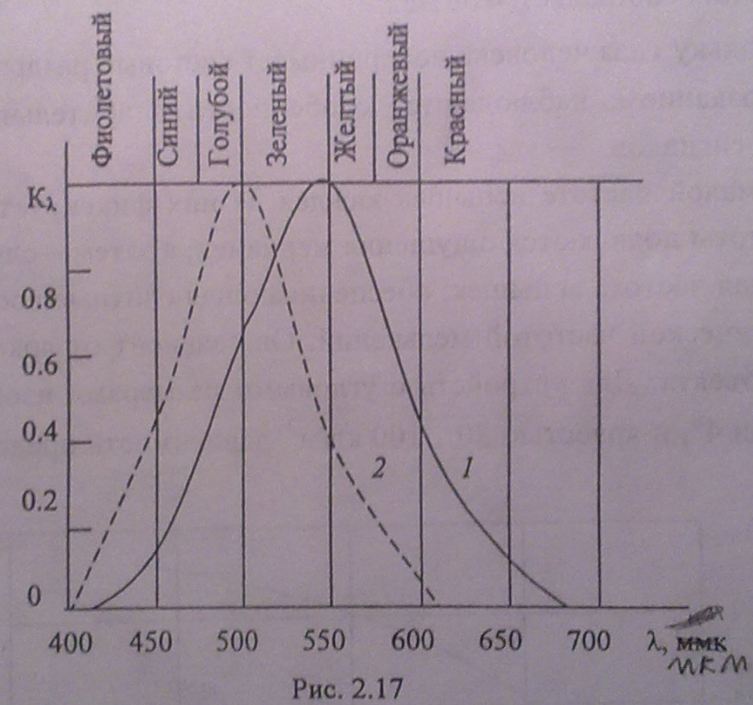
По мере удаления от зоны с наибольшей чувствительностью (желто- зеленый цвет) зрительные ощущения монотонно убывают вплоть до своего исчезновения.

Как следует из графика, зрительный аппарат человека-оператора при дневном освещении наиболее чувствителен к «зеленому» цвету, а при ноч­ном к «синему». Именно это обстоятельство определяет выбор цветовой гаммы индикаторов, предназначенных для преимущественного использова­ния в разное время суток.

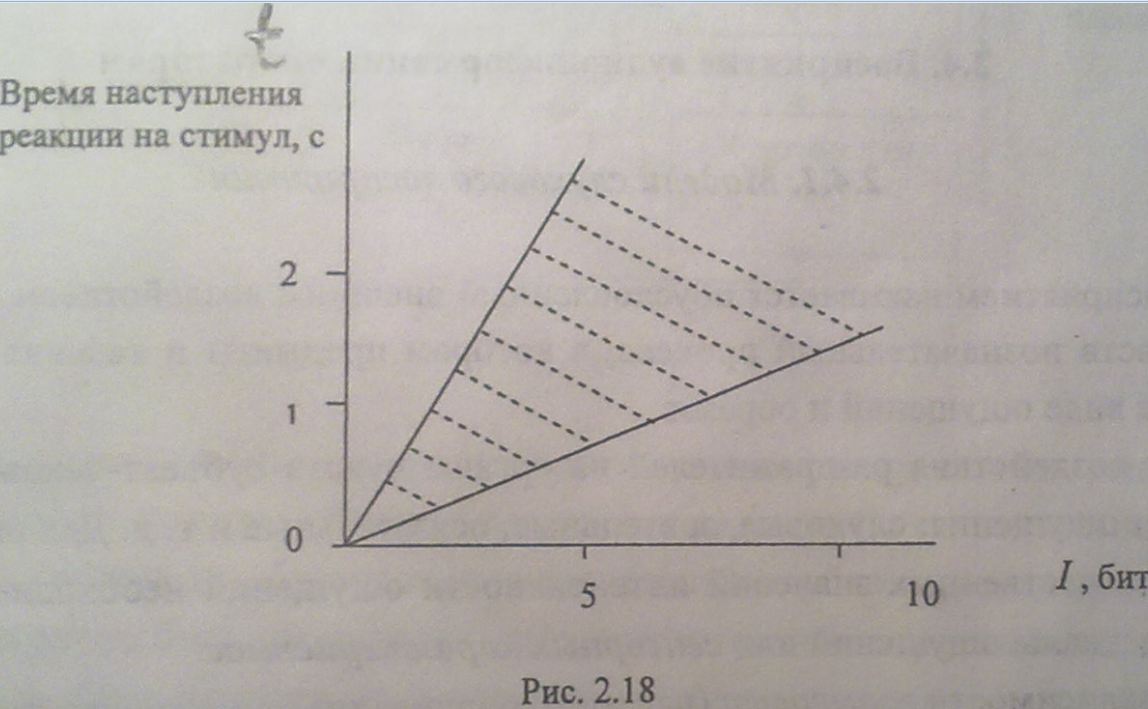
С увеличением количества предъявляемой информации время ее перера­ботки возрастает, т. е. «пропускная способность» оператора остается практически постоянной (рис. 2.18).Как следует из графиков, указанная зависимость имеет практически линейный характер. Ясно, что в связи с индивидуальными особенностями наблюдается «разброс», отраженный на графике в виде соответствующего штрихованного поля. Поскольку «пропускная способность» является факти­чески «производной» от приведенной линейной зависимости, это обосновы­вает тезис о практическом постоянстве возможностей оператора по усвоению представляемой информации. Ω=∂I/∂t=const

27. Линейные характеристики звукового поля.

Звуковое поле - одна из форм существования материи, проявляемая в виде кинетической и потенциальной энергии, колеблющихся материальных тел. Частоты звуковых колебаний находятся в полосе частот от 20 до 20000Гц.

Колеблющееся тело, являющееся источником звука, приводит в движение примыкающие к нему частицы упругой среды, которые, в свою очередь, заставляют колебаться соседние с ним частицы. Процесс распространения колебаний в упругой среде называют волной. Направление распространения звуковых волн называют звуковым лучом, а поверхность, соединяющую все точки с одинаковой фазой колебания частиц - фронтом волны. Фронт волны в каждый момент времени перпендикулярен звуковому лучу.

Расстояние между двумя соседними сгущениями (разрежениями) называется длиной волны . Разность между мгновенным давлением звукового поля в данной точке и статическим (атмосферным) называют звуковым давлением: . Звуковое давление - величина знакопеременная. В моменты сжатия среды оно положительно: > , а в момент разряжения - отрицательно, т.е. < .

Звуковое давление в системе СИ измеряется в Паскалях. Давление в 1 Паскаль (Па) создается при действии силы в 1 ньютон (Н) на поверхность площадью 1м². Ясно, что 1 Па в 10⁵ раз меньше 1 атмосферы. Скорость распространения звука в воздухе сильно зависит от метеорологических условий и температуры. В последнем случае с достаточной для практики точностью можно записать: , где Т – абсолютная температура, а размерность скорости звука – м/с.

28. Уравнение движения сплошной среды при передаче звука.

Расстояние между двумя соседними сгущениями называется длиной волны . Разность между мгновенным давлением звукового поля в данной точке и статическим (атмосферным) называют звуковым давлением: .

Колебательное движение частиц среды при распространении звуковой волны характеризуется также колебательным смещением (от положения покоя), которое происходит с определенной скоростью, именуемой колебательной: . Производная по времени от колебательной скорости образует колебательное ускорение.

Колебательную скорость считают положительной, если частицы среды смещаются в направлении движении волны, и отрицательной, если эти движения встречные. Если источник звука совершает колебания по гармоническому закону с линейной частотой f, то за время T, в течение которого происходит один период колебательного процесса, фронт звуковой волны перемещается на расстоянии, численно равное длине волны - . Очевидно, что одну секунду волна распространится на расстояния численно равные .

Выделим в звуковом поле элементарный объем воздуха, заключенный между боковыми поверхностями , находящимися на расстоянии друг от друга перпендикулярными к направлению звуковых лучей.

Масса воздуха в выделенном объеме равна , где - плотность среды. Среда в рассматриваемом объеме находится под действием разности давлений и . Следовательно, сила, под действием которой может происходить движение этого объема воздуха: .

Если под действием приложенной силы элементарный объем воздуха с массой приобретает ускорение ∂V/∂t, то по второму закону Ньютона сила инерции: , откуда переходя к производным, устремив , получим: . (3.1)

Данное уравнение и называют уравнением движения среды при прохождении звука. При такой записи учитывается только одномерное движение по координате x. При трехмерном движении, получим:

где - единичные векторы – орты осей декартовой системы координат.

29. Характеристики поля плоской волны.

Колебательный процесс, распространяющийся в среде в виде волны, фронт которой представляет собой плоскость, называется плоской звуковой волной.

Если излучатель (поршень) совершает колебания по гармоническому закону с частотой , а размеры поршня (диаметр волновода) значительно меньше длины звуковой волны, то давление, создаваемое около его поверхности, . Очевидно, что на расстоянии х давление будет , где – время пробега волны от излучателя до точки x. Это выражение удобнее записать, как: , где - волновое число распространения волны. Произведение - определяемый фазовый набег колебательного процесса в точке, удаленной на расстояние х от излучателя.

Подставляя полученное выражение в уравнение движения (3.1), проинтегрируем последнее относительно колебательной скорости:

Вообще для произвольного момента времени оказывается, что: . (3.9)

Правая часть выражения– характеристическое, волновое, или удельное акустическое сопротивление среды (импеданс). Как следует из решения, полученное уравнение справедливо в поле плоской волны.

Помимо скалярного потенциала, давления и колебательной скорости звуковое поле характеризуется и энергетическими характеристиками, важнейшей из которых является интенсивность - вектор плотности потока энергии, переносимой волной за единицу времени. По определению - есть результат произведения звукового давления на колебательную скорость.

30. Волновое уравнение Диссипация энергии.

ДИССИПАЦИЯ ЭНЕРГИИ - переход части энергии упорядоченных процессов в энергию неупорядоченных процессов, в конечном счёте - в теплоту.

В теоретической акустике показано, что при учете адиабатического характера звукового процесса для газовой среды уравнение может быть преобразовано в волновое уравнение: , где - скорость распространения звука в газовой среде; - оператор-лапласиан. Волновое уравнение может быть записано также для давления и колебательной скорости звука. Для гармонических процессов, протекающих с частотой , волновое уравнение можно преобразовать в уравнение Гельмгольца: , где - волновое число. Общее решение уравнения Гельмгольца имеет вид: .

В уравнении каждое слагаемое соответствует волне, распространяющейся в «положительном» или «отрицательном» направлении оси «х». Выбор знака зависит от выбора знак во «временном» множителе .

31. Волны с неплоскими фронтами.

У сферической волны поверхность равных фаз является сферой. Источником такой волны также является сфера, все точки которой колеблются с одинаковыми амплитудами и фазами, а центр остается неподвижен (см. рис. 3.4, а).

Сферическая волна описывается функцией, являющейся решением волнового уравнения в сферической системе координат, для потенциала волны, распространяющейся от источника: .

Действуя по аналогии с плоской волной, можно показать, что на расстояниях от источника звука значительно больше длины изучаемых волн: .«точечный» источник излучает, преимущественно, сферические волны. На больших расстояниях от источника или, как принято говорить, в «дальней» зоне сферическая волна применительно к ограниченным по размерам участкам волнового фронта ведет себя как плоская волна. Требования к малости участка определяются не только частотой, но - разностью расстояний между сравниваемыми точками. Отметим, что указанная функция имеет особенность: при . В свою очередь цилиндрические волны (поверхность волнового фронта - цилиндр) излучаются бесконечно длинным пульсирующим цилиндром .В дальней зоне выражение для функции потенциала такого источника асимптотически стремится к выражению :

 .(3.12)

Можно показать, что и в этом случае выполняется соотношение .

32. Преломление плоской упругой волны на границе раздела двух сред. Коэффициенты отражения и прохождения по давлению.

Граничное условие первого типа:

1. Равенство давлений по обе стороны границы (3.14)

Граничное условие второго типа:

2. Равенство нормальных компонент упругих смещения и колебательных скоростей, с учетом : . (3.15)

Для удобства вычислений безразмерных выражений введем дополнительные обозначения: ,(3.16) коэффициент отражения по давлению; ,коэффициент прохождения по давлению.

Подставив полученные выражения для системы волн в граничные условия, получим систему двух уравнений с двумя неизвестными R и D.

Решение этой системы: при - «нормальное» падение: , . (3.19)

При этом было учтено, что по закону Снеллиуса: еденицы (3.20)

Если в выражениях перейти к колебательным скоростям, то можно получить выражения для коэффициентов отражения и прохождения по колебательной скорости:

.

33. Виды коэффициентов отражения упругой волны на границе раздела двух сред. Частные случаи соотношений параметров сред.

Граничное условие первого типа:

1. Равенство давлений по обе стороны границы (3.14)

Граничное условие второго типа:

2. Равенство нормальных компонент упругих смещения и колебательных скоростей, с учетом : .

коэффициент отражения по давлению; коэффициент прохождения по давлению.

Выражения для коэффициентов отражения и прохождения соответственно по колебательной скорости: , .

Рассмотрим частные случаи соотношения импедансов прилегающих сред, от которых зависят значения, принимаемые выведенными коэффициентами:

1. абсолютно «мягкая» граница (вода – воздух): (3.23)

2. абсолютно «жесткая» граница : (3.24)

Коэффициенты отражения и прохождения для разных физических величин могут для одинаковых сочетаний сред принимать разные значения.

Коэффициенты отражения и прохождения для разных физических величин не зависят от частоты.

Рассмотренные частные случаи фактически определяют различия между двумя предельными состояниями «граничных» условий, широко используемых в «краевых» задачах математической физики:

Первое условие Дирихле, иначе называемое условием на абсолютно «мягкой» или «свободной» границе: (3.25)

Второе условие Неймана, иначе называемое условием на абсолютно «жесткой» границе: (3.26)

34. Преломление плоской упругой волны на границе раздела двух сред. Отражение от плоского слоя.

Граничное условие первого типа:

1. Равенство давлений по обе стороны границы (3.14)

Граничное условие второго типа:

2. Равенство нормальных компонент упругих смещения и колебательных скоростей, с учетом : . (3.15)

Выражения системы (3.27) необходимо подставить в граничные условия: , (3.28)

где ; ; .

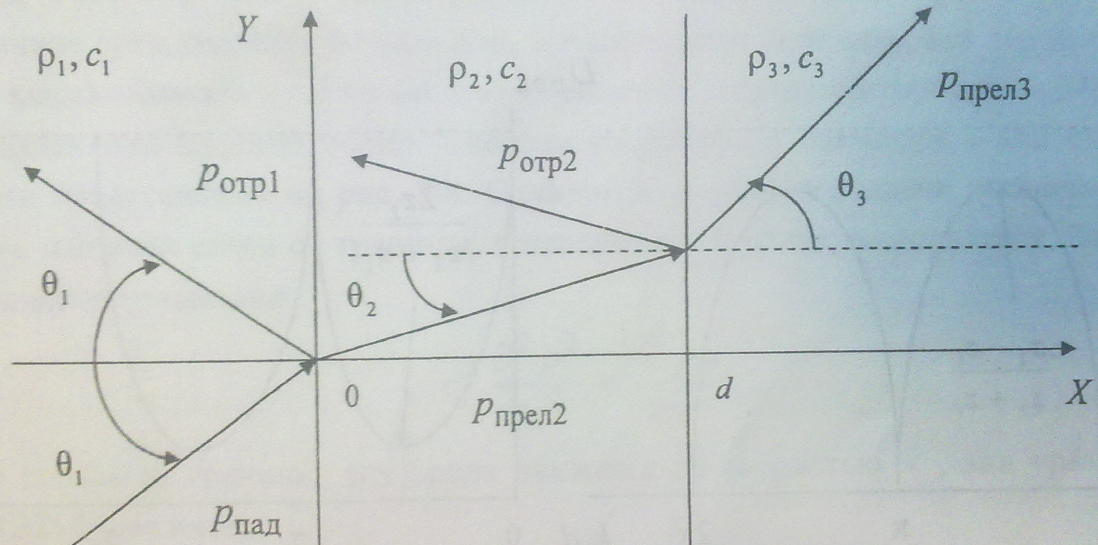
Здесь выполняется закон Снеллиуса: . (3.29)

Для упрощения преобразований введем безразмерные величины коэффициентов отражения и прохождения , для которых, в частном случае , можно показать, что: ,(3.30)

, (3.31) где - так называемый «наклонный» импеданс. В качестве примера рассмотрим графики зависимостей (3.30, 3.31) от волновой толщины слоя при значении угла падения (нормальное падение, см. рис. 3.7а, б).

Как видно из графиков, зависимости имеют осциллирующий характер. Коэффициент отражения обращается в нуль при значениях волновой толщины, кратных , где .

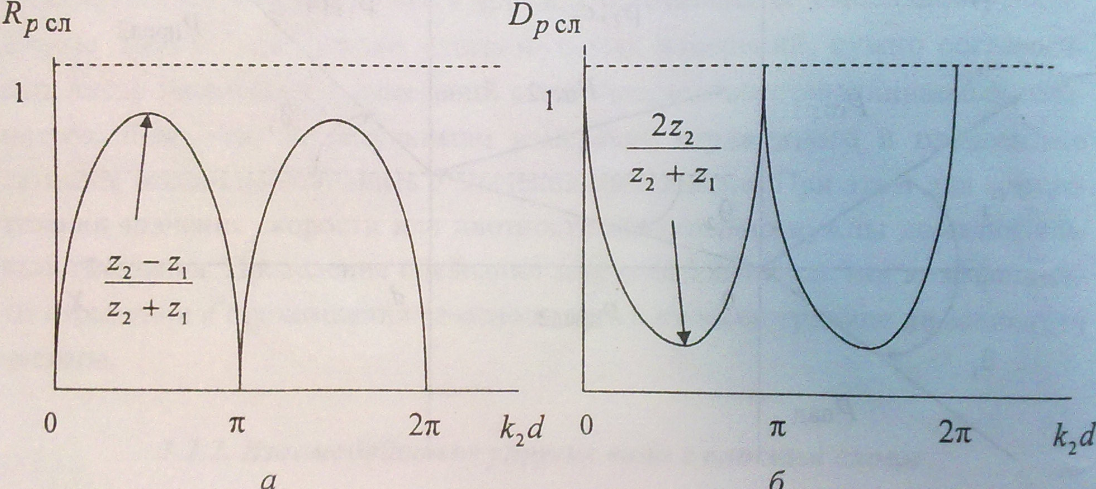Рис. 3.7

При этих же значениях волновой толщины коэффициент прохождения становится равным единице. При значениях волновой толщины, кратных , значения коэффициента отражения достигают максимума, равного значению коэффициента отражения от плоской границы. При этих же значениях волновой толщины коэффициент прохождения получает минимальные значения, равные коэффициенту отражения от плоской границы. Кроме того, коэффициент отражения от слоя обращается в нуль при равенстве импедансов слоя и окружающей среды: . Существует и еще одно условие равенства нулю коэффициента отражения независимо от волновой толщины слоя: - случай так называемого «просветляющего» слоя.

35. Преломление плоской упругой волны на границе раздела двух сред. Отражение от подвижной среды.

Одна из прилегающих к границе сред является подвижной.

Отличие в постановке задачи заключается в том, что если слева от границы, в неподвижной среде, выполняется обычное волновое уравнение: , то, справа от границы, где среда подвижна, вид уравнения будет иной: .

Выражение для закона Снеллиуса примет вид: , при следует, что

После подстановки выражений для волновых функций (3.13) в граничные условия (3.14 , 3.15), можно показать, что при и , выражения для коэффициентов отражения и прохождения: , .

36. Эффект полного внутреннего отражения.

Пусть скорость звука во 2-ой среде будет меньше, чем в 1-ой среде , тогда из закона Снеллиуса следует, что .

Устремим значение угла падения , тогда можно утверждать, что выполнимо неравенство .

Пусть скорость звука во второй среде больше скорости звука в первой среде: , тогда будет принимать следующие значения: при для , , а при , . Итак, при , . Найдем значения для вычисления наклонного импеданса: ,

где - вещественная величина.

Перейдем теперь к рассмотрению величин коэффициента отражения . Подставляя в формулы выражения получим:

где . Из выражения следует, что модуль коэффициента отражения равняется единице (отсюда название - «полное» отражение), а отраженная волна приобретает дополнительный фазовый сдвиг по сравнению с падающей.

Рассмотрим, теперь, поведения коэффициента прохождения . Используя выражение получим:

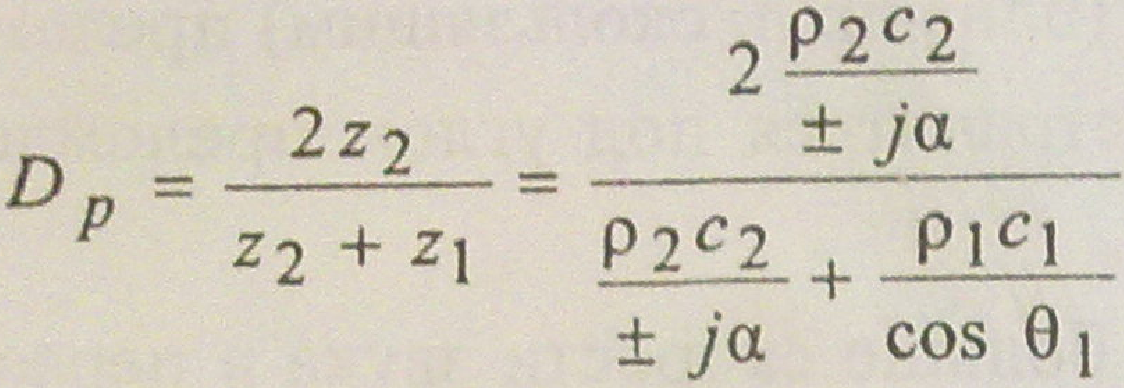
где фазовый сдвиг . Видно, что «просачивание» волны через границу все же происходит, и модуль коэффициента прохождения отличен от нуля при наличии дополнительного фазового сдвига. Попытаемся выяснить физический смысл появляющегося волнового процесса. Запишем более подробно выражение для волны давления во второй среде:

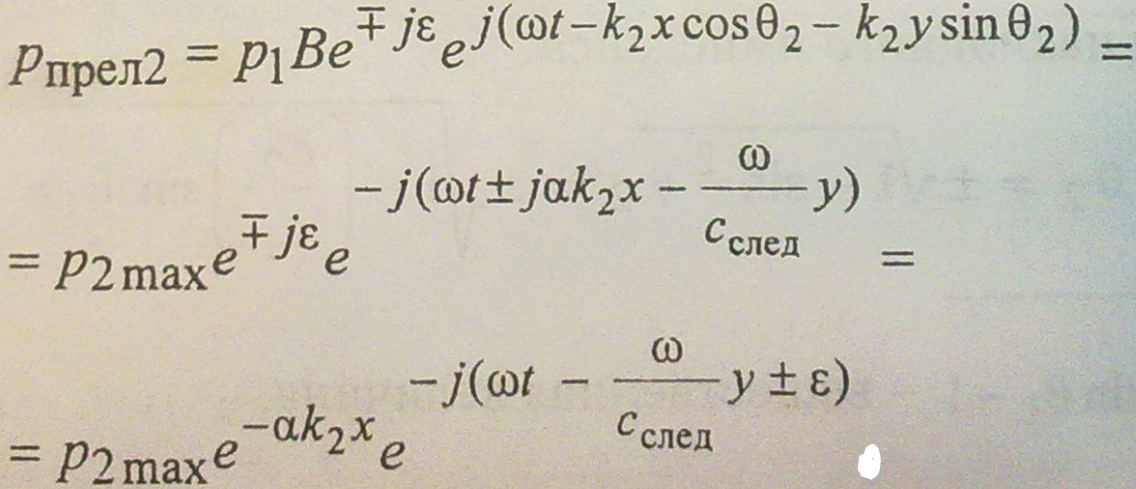
где - скорость следа (скорость пересечения фронтом падающей волны границы сред).

40. Эффект Доплера. Подвижный излучатель, неподвижный приемник.

Эффект Доплера заключается в том, что в результате взаимного перемещения источника и приемника звука относительно неподвижной акустической среды, частота сигнала, фиксируемая приемником, отличается от частоты сигнала, излученного источником.

Пусть источник звука –излучатель (И) движется из точки А в точку Б. Движение И происходит со скоростью V_изл под углом  относительно линии соединения точек А и Б.

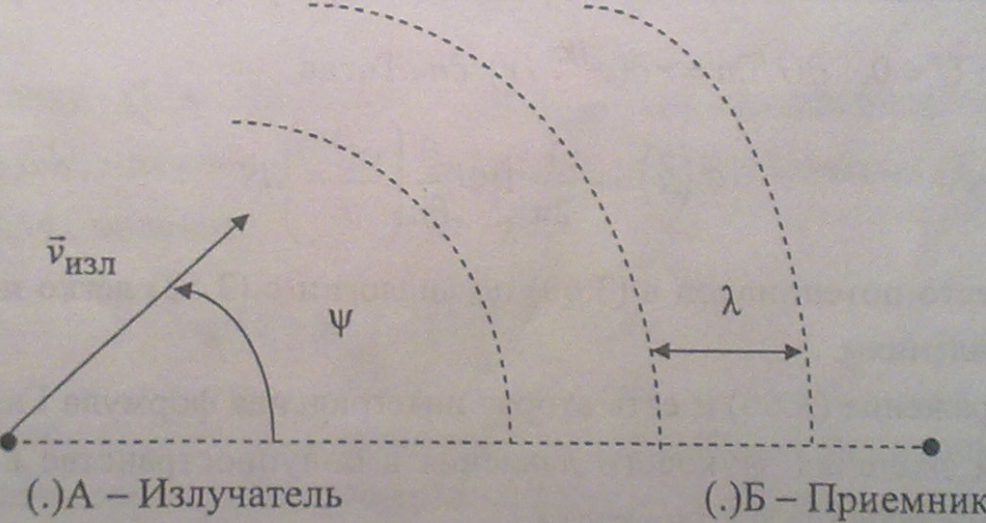
Источник, двигаясь в указанном направлении, периодически создаёт сжатие и разрежение среды, которые в направлении от (∙) А и (∙) Б будут сближаться, а в направлении от (∙) Б к (∙) А (слева от точки (.) А)– удаляться друг от друга. Если излучатель перемещается, то приемник будет реагировать на измененную длину волны и более короткую, чем приемники, расположенные по всем другим направлениям по сравнению с φ=0.

Т.к., обычно скорость движения излучателя значительно меньше скорости звука в среде, то приближенно: .

Эффект Доплера в рассмотренном случае физически обусловлен “деформацией” акустического поля за счет движения источника. Для сохранения частоты принимаемого сигнала И должен двигаться по круговой траектории.

41. Эффект Доплера. Неподвижный излучатель, подвижный преемник.

Приемник с большей частотой встречается с волновыми фронтами.

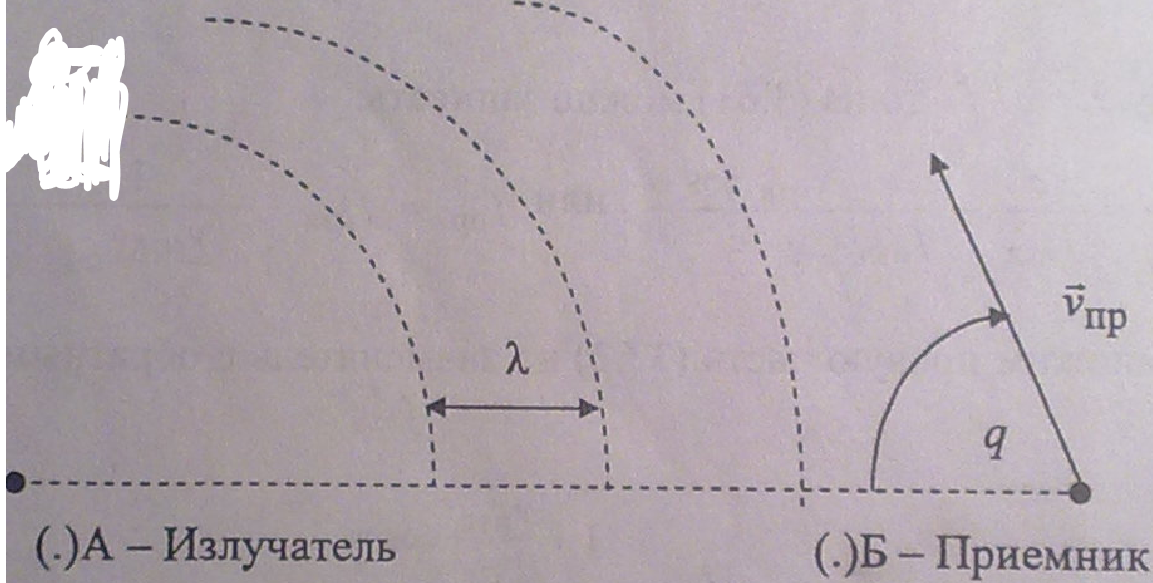
Формула для определения частоты принимаемого сигнала. Равенство является строгим: . (3.64)

Поэтому при q = 0 и  с, частота принимаемого сигнала стремится к удвоенному значению по сравнению с частотой излучаемого сигнала. При движении И и П по кругу, частота принимаемого сигнала изменяться не будет.

42. Эффект Доплера. Подвижный излучатель и приемник.

Сигналы, поступающие от обоих объектов, перемножаются и для частоты приема можно на основании результатов, полученных для двух предшествующих вариантов, записать точное соотношение: . (3.65)

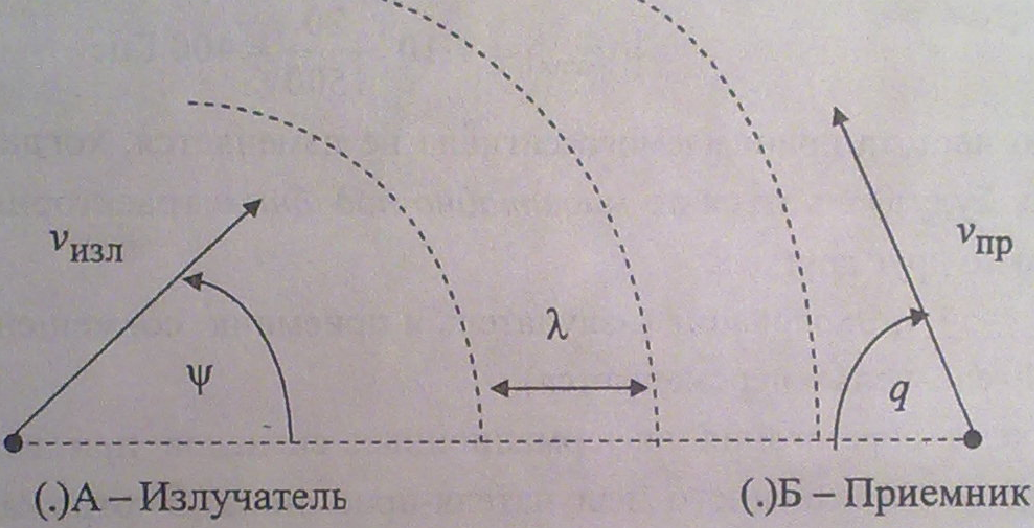
Очевидно, что при малости скорости движения излучателя по сравнению со скоростью звука: , тогда (3.65) превратится в: ^.

Раскрываем скобки и, учитывая , получим: .(3.66)

Таким образом, отклонение частоты носит знакопеременный характер. Его величина определяется формулой: Максимальное отклонение частоты при φ=0, q = 180º и φ=180º, q = 0 составит: .

При движении И и П параллельно друг другу, частота принимаемого сигнала изменяться не будет.

43. Эффект Доплера в режиме эхо-локации.

Эхолокация ( И + П – совмещены на подвижном носителе , цель – осуществляет перемещение).

При приеме эхо-сигнала изменение частоты из-за эффекта Доплера будет выражено более сильно, чем при прямом обмене. Причина этого в том, что падение акустической волны на препятствие и отражение от него можно отождествить с излучением и приемом «вторичных» волн.

Тогда точным выражением для изменения частоты сигнала будет: .

Пренебрегая величинами второго порядка малости и учитывая, что : Тогда, максимальное отклонение частоты

44. Рассеяние звука на шероховатой поверхности.

Достаточно часто приходиться встречаться с отражением упругих волн от поверхностей, отличающихся различной степенью неровности.

При отражении звука от шероховатых поверхностей наряду с зеркально отраженной волной возникают и компоненты рассеяния в других направлениях, определяемых соотношениями длины волны и параметров поверхностей.

Учет влияния указанных компонент – в общем случае задача сложная. Сравнительно просто её можно решить при выполнении определенных условий, накладываемых на св-ва поверхности.

1.Средняя высота (амплитуда) шероховатостей много меньше длины волны звука (диффузное рассеяние);

2. Протяженность неровностей вдоль поверхности и их радиуса должно быть много больше длины волны звука ( ).

Количественный критерий для описания условий рассеяния определяется параметром Рэлея: , где - волновое число, - средняя высота неровностей,  - угол падения плоской волны. Для диффузного рассеяния  1.

Волновой процесс в окрестности периодически шероховатой (волнистой) поверхности в плоскости xz: , (3.43)

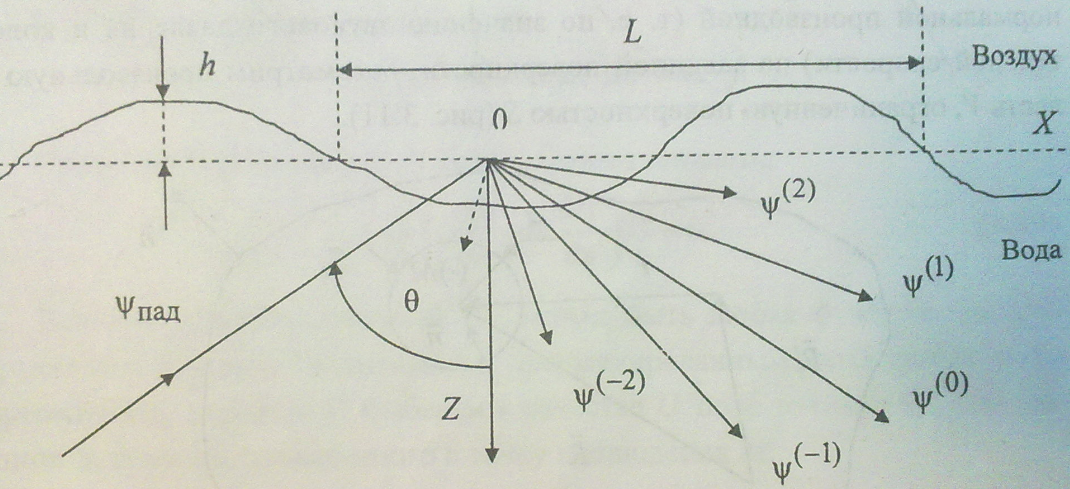
Решение для произвольного приближения имеет вид: (при этом временной множитель учитывать не будем):

При , кроме зеркально отраженной волны образуется система дифракционных «пучков» - угловых спектров с амплитудами, спадающими по закону . При учете энергии, уносимой только волной «нулевого спектра», коэффициент отражения от неровной поверхности определяется выражением . Именно образование «дифракционных» пучков-спектров и является причиной диффузного рассеяния. Один из этих «спектров» может совпасть с падающей волной, образуя обратно отраженную волну.

45. Интеграл Кирхгофа.

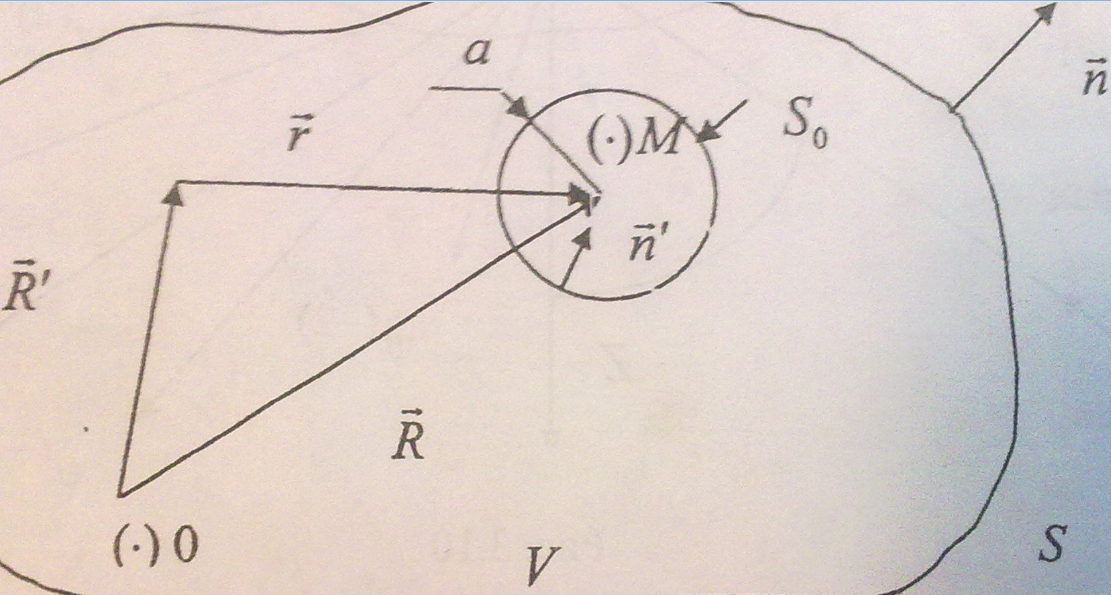
Требуется найти связь между значением Ф в некоторой области пространства V для точки наблюдения (.) М и значением Ф на поверхности S. Такая связь может быть получена путем использования формулы Грина.

Формула Грина: любые две ф-ии Ф и U, непрерывные вместе со своими первыми и вторыми производными в области V, удовлетворяют соотношению .n – внешняя нормаль. внутри объема V существует два звуковых поля, описываемых функциями Ф и U, которые удовлетворяют уравнению Гельмгольца: .

Звуковое поле Ф – это основное поле, которое требуется определить; поле U является вспомогательной величиной. Звуковое поле Ф в уравнении Гельмгольца умножим на U, а второе уравнение - на Ф, затем вычтем второе уравнение из первого и сумму проинтегрируем по объему V.

.

Применяя к последнему выражению формулу Грина, можно записать:

Выберем в качестве U поле точечного ненаправленного источника, помещенного в точке наблюдения М. (3.50),где , - радиус вектор, проведенный от начала координат в точку наблюдения М; - радиус вектор, направленный в любую точку поля.

В сферической системе координат в силу симметрии задачи уравнение Гельмгольца можно записать в виде: . (3.51)

Прямой подстановкой легко установить, что функция удовлетворит этому уравнению.

Окружим точку М малой сферой S₀ радиуса а. Новая область будет расположена между S и S₀, а полная новая поверхность, ограничивающая объем, будет состоять из двух частей S и S₀.

Рассмотрим интеграл по поверхности S₀. Наружная к области нормаль к поверхности S₀ будет направлена внутрь сферы S₀. Из-за этого на S₀ имеем . Сколь бы малым ни выбиралось значение радиуса окружности - а, величины U и на поверхности будут оставаться конечными, так что применение формулы Грина является допустимым.

Вычислим: . (3.52)

Поскольку искомое поле является непрерывной функцией координат в любой точке области, то в пределах малой сферы радиуса а, можно считать, что Ф и мало зависит от положения точки на поверхности S₀. Поэтому Ф и можно вынести из под знака интеграла, заменив их значения в точке, определенной вектором . Для функции Ф этого сделать нельзя, так как внутри S₀ она обладает особенностью.

В результате можно записать: .

Учитывая, что на поверхности S₀:

где – элемент телесного угла, получим:

Отметим, что поверхность интегрирования является суммой S и S₀. Тогда получим, что , откуда: .

Так как интегрирование проводится по поверхности S, то величины r в этой формуле являются расстоянием от точки наблюдения М до элемента поверхности S.

Полученное выражение носит название формулы Кирхгофа или интеграла Кирхгофа.

46. Интегральные формулы Гюйгенса.

. формула Кирхгофа или интеграл Кирхгофа.

Запишем формулу интеграла Кирхгофа в виде. . (3.54) где U – вспомогательная функция, представляющая собой поле точечного источника. Выберем в качестве U функцию, которая описывает поле точечного источника, расположенного над абсолютно жесткой поверхностью. в точке М поле от источника, помещенного в произвольную точку над плоскостью может быть представлено в виде суммы полей источника Q и зеркально расположенного источника Q’:

.

Нормальная производная этого поля определяется выражением: .

Устремим точку Q к границе. Учитывая, что на границе r1=r2=r, , получим . Подставляя эти значения в формулу, получим: .

Выражение называется первой интегральной формулой Гюйгенса. Здесь для расчета звукового поля во всем полупространстве требуется знать только одну величину , т.е. колебательную скорость поверхности. Перейдем от потенциалов к колебательной скорости и звуковому давлению: ; . Тогда: p( ) =

Полученное выражение служит основной формулой для расчета звуковых полей плоских излучателей и приемников звука. Для того, чтобы получить вторую интегральную формулу Гюйгенса, следует в качестве вспомогательной функции выбрать поле точечного, ненаправленного источника, расположенного над абсолютно мягкой поверхностью. В этом случае поле мнимого источника Q’ будет противоположно по знаку полю источника Q: Вычислив производную и устремив точку Q к границе, получаем: . Тогда: Ф( ) = .

Это выражение и есть вторая интегральная формула Гюйгенса, определяющая значения звукового давления в полупространстве по известной величине звукового давления на плоскости.

37. Модели и свойства слухового восприятия.

Восприятием называется обусловленный внешним воздействием на ор­ганы чувств познавательный процесс, в котором предметы и явления отра­жаются в виде ощущений и образов.

От воздействия раздражителей на органы чувств субъект-человек ис­пытывает ощущения: слуховые, зрительные, осязательные и т. д. Для опреде­ления количественных значений интенсивности ощущений необходимо по­строение шкалы ощущений или сенсорных характеристик: 1)зависимости громкости(параметр ощущения) от звукового давления или интенсивности звука (физической величины); 2)зависимости высоты тона от частоты сигнала; 3)зависимости громкости звукового импульса от его длительности при постоянстве звукового давления.

Рассмотрим прохождение сигналов в модели процесса восприятия слу­хового образа (рис. 2.19). Согласно схеме субъект взаимодействует с систе­мой входных и выходных процессов (сигналов). Со стороны входа на субъект действуют исходящие от окружающих предметов раздражители - стимулы, имеющие физическую природу.

Раздражители (стимулы) - только те физические воздействия, которые могут быть восприняты органами чувств субъекта и породить ощущения. Множество входных сигналов, т. е. стимулов, называют полем восприятия (перцептивным полем).

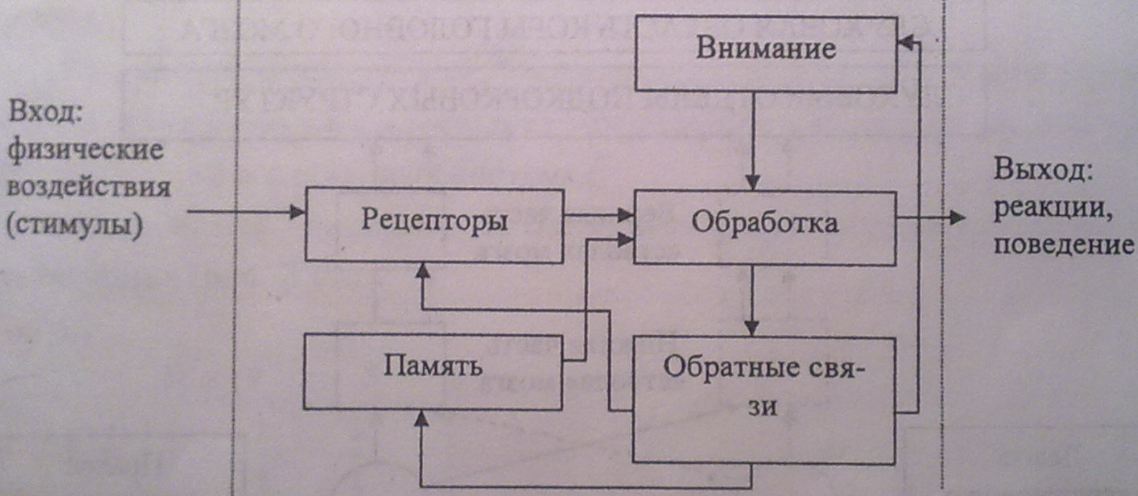
Приемниками стимулов являются специализированные рецепторы, совокупность которых образует рецепторные поля. Со стороны выхода воз­никают реакции на обусловленные восприятием субъекта входные стимулы. Реакции могут быть созерцательными, мыслительными, речевыми или двига­тельными. Прохождение сигналов в слуховой системе человека можно отобразить виде структурной схемы (рис. 2.20).

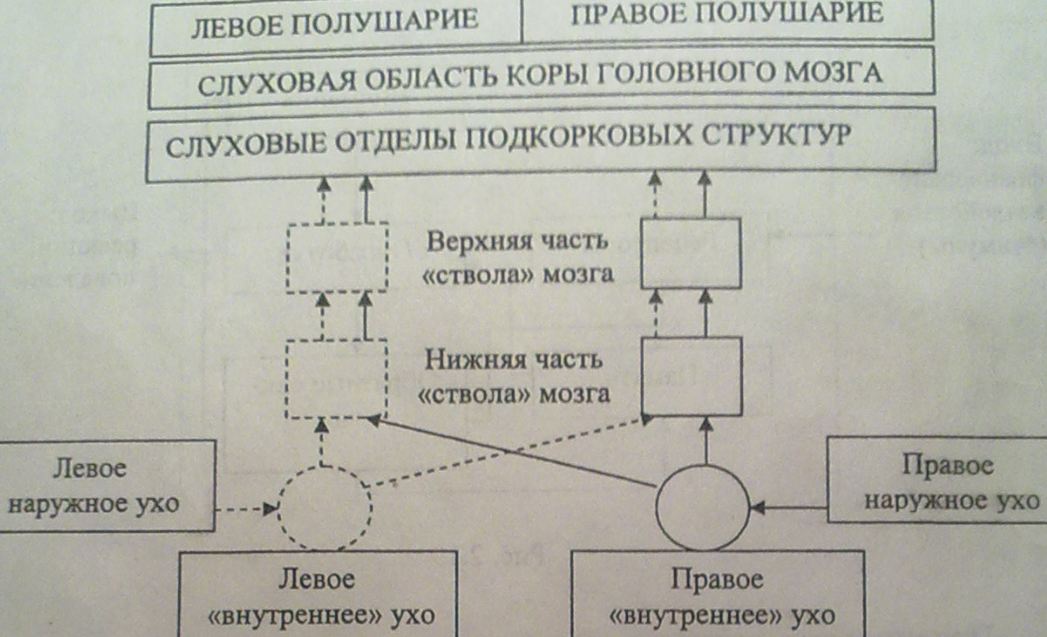
Воспринимаемые сигналы поступают в слуховую кору головного мозга по каналам связи, каковыми являются нервные волокна. На своем пути они встречают промежуточные центры распределения и обработки информации: 1)«внутреннее» ухо («улитковые» ядра); 2)нижняя часть ствола мозга (верхние оливы); 3)верхняя часть ствола мозга.

Информация, поступающая по слуховому нерву от правого уха к пра­вому «улитковому» ядру, распределяется в нем так, что большая ее часть пе­редается в левую верхнюю оливу и оттуда - в левое полушарие головного мозга. Меньшая часть информации через правую верхнюю оливу передается в правое полушарие. Аналогично распределяются сигналы из левого уха. В слуховых отделах головного мозга происходит первичная обработка звуко­вых сигналов: определяется высота тона, громкость и некоторые признаки тембра. Выше, в слуховой коре идут сложные процессы, многие из которых не являются врожденными, а формируются в процессе общения с людьми и природой.

38. Строение и свойства слуховых сенсоров.

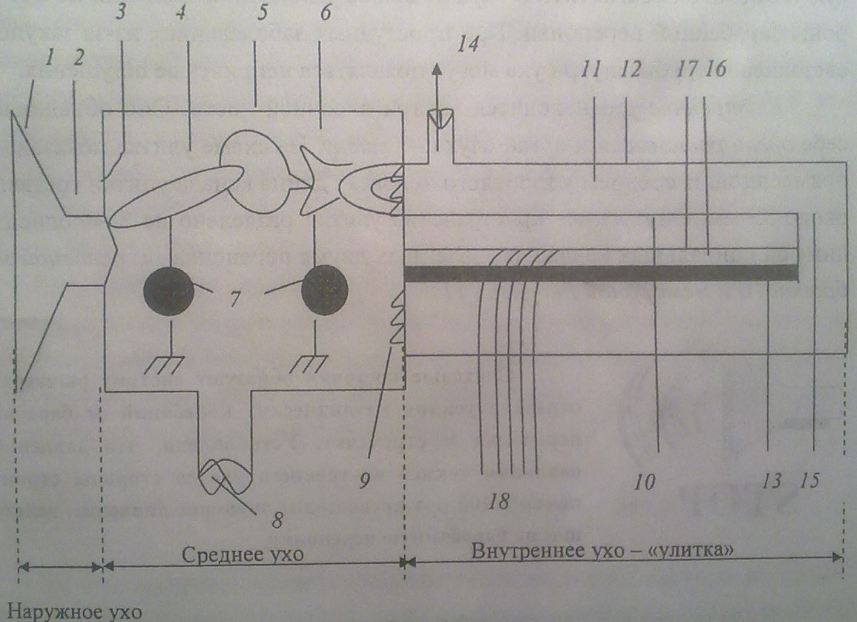
Звуковые волны принимаются акустической «рупорной» антенной - ушной раковиной I и через слуховой «ход» 2, который служит коротким вол­новодом, воздействуют на барабанную перепонку> 3.

Барабанная перепонка вогнута внутрь уха и натянута. В полости среднего уха (барабанной полости) расположены 3 слуховые косточки: молото­чек 4, наковальня 5 и стремечко 6, шарнирно соединенные между собой суставами и оснащенные поддерживающим мышечным аппаратом 7.

Рукоятка молоточка прикреплена к барабанной перепонке, а мышца последней поддерживает ее в натянутом состоянии. Основание «стремени» закрывает собой овальное окно, за которым находится внутреннее ухо. Стре­мя в овальном окне закреплено нежестко и может совершать возвратно-поступательные движения. Слуховые косточки образуют систему рычагов для передачи усилия механических колебаний от барабанной перепонки к стремечку. Установлено, что давление на овальном «окне» внутреннего уха со стороны стремечка почти в 100 раз превосходит звуковое давление, дейст­вующее на барабанную перепонку. Евстахиева труба 8 соединяет барабан­ную полость с носоглоткой и служит для выравнивания давлений по обе сто­роны барабанной перепонки. При простудных заболеваниях из-за закупорки евстахиевой трубы внутри уха могут появляться неприятные ощущения.

Внутреннее ухо находится внутри височной кости. Оно объединяет в себе орган равновесия и орган слуха - улитку. На схеме улитка показана вы­прямленной. В среднем у взрослого человека длина канала улитки составляет около 35 мм. Внутреннее пространство улитки разделено на 3 заполненных лимфой спиральных канала, разделенных двумя перепонками: основной мем­браной 10 и мембраной Рейснера 11.

Из-за сходства с «винтовыми» лестницами эти каналы называют: лест­ницей «преддверия» 12; «срединной» лестницей 13 и лестницей «барабан­ной» 14. Между лестницей «преддверия» и барабанной полостью находится овальное «окно» («окно» преддверия), в котором расположено основание стремечка, а между лестницей барабанной и барабанной полостью - «окно» круглое 9 улитки, закрытое упругой мембраной.

Срединная лестница заполнена вязкой биологической жидкостью - эндолимфой, а две другие - перилимфой. Эндолимфа обладает значительно бо­лее высокой вязкостью и плотностью, чем перилимфа. Полости, заполненные перилимфой, сообщаются между собой через отверстие-канал, расположен­ный вблизи от вершины улитки - геликотрему 15.

Основная мембрана представляет собой аморфную ненатянутую пере­понку, закрепленную по краям. Длина ее (для взрослого человека) составляет примерно 32 мм, ширина у основания - 0.1 мм, а возле геликотремы - 0.5 мм. Со стороны эндолимфы на основной мембране расположен кортиев орган 16 с покровной мембраной 17. Кортиев орган - это множество (около 4000) «волосковых» клеток, чувствительных к давлению и деформации основной мем­браны.

С волосковыми клетками контактируют основания нервных волокон, соединенных в пучок и образующих слуховой нерв 18, связанный с «ядрами» ствола головного мозга. Субъективные ощущения высоты звука тем выше и громкости тем больше, чем, соответственно, ближе к основанию основной мембраны находится область с максимальной амплитудой колебаний и чем больше амплитуда смещений тканей мембраны.

39. Слух и восприятие звуковых сигналов.

Слуховой анализатор можно уподобить особому преобразователю, где со стороны входа параметрами сигнала являются звуковое давление и частота, а со сто­роны выхода - «громкость» и «высота» тона.

Экспериментально получены сенсорные характеристики передачи «чистых тонов» слуховой системой человека, т. е. в установившемся режиме при достаточно продолжительном звучании измерительного сигнала.

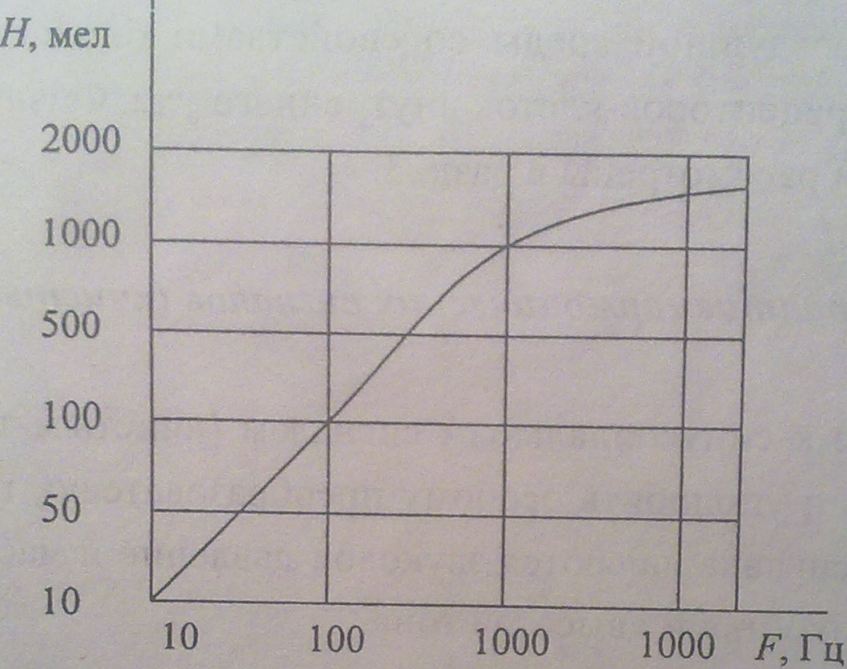
Идеализированными моделями таких сигналов условно являются сигналы гармонического типа. Существует несколько принципов построения измерительных шкал Н (высоты тона) от F (частоты звука) для таких сигна­лов: 1)Шкала Г. Флетчера: частоте 1000 Гц соответствует высота тона в 1000 мел (1 мел - единица измерения высоты тона). На практике эта шкала не всегда удобна. 2)Шкала Э. Цвиккера: частоте 131 Гц (нота «до» малой октавы) соот­ветствует высота в 131 мел. 3)Музыкальная шкала: в ее основе лежит тональный интервал в одну

октаву, при которой верхняя частота F_В вдвое превышает нижнюю частоту F_Н, т. е. F_B/F_H = 2. Интервал частот F₁ и F₂ в октавах равен F₁ — F₂ = log₂F1/F2. Октава делится на 12 полутонов так, что в каждом полутоне частоты соотносятся между собой как F_B/F_H = . Каждый полутон делится на 100 центов. Высота полутонов имеет свои обозначения (нотацию) — до (С), ре (D), ми (Е), фа (F), соль (G), ля (А), си (В) с указанием октавы (большая, малая, первая и т. д.) и с добавлением знаков альтерации (бемоль, диез, бе­кар). Диапазон 20 Гц...20 кГц составляет около 10 октав. Примерный вид сенсорной характеристики «высоты» тона по шкале Цвиккера представлен на рис. 2.22.

На рис. 2.23 изображены стандартные кривые равной громкости («изо­фоны») при прослушивании чистых тонов. За «пороговое» значение принято р_зв =2 *10^-5 Па, называемое стандартным порогом слышимости на частоте 1000 Гц. Легко показать, что значение «пороговой» интенсивности звука составит

I_O=p₀ ²/ρ_воздс_возд≈10^-12 Вт/м². Относительное значение слышимости, дБ, определяется по формуле N = 20lg p_зв/p₀, где p_зв - «пороговое» значение давления.

В качестве примеров на рис. 2.23 приведены: 1 - линия «порога» слы­шимости; 2 - линия «порога» болевого ощущения, за пределами (выше) которой возможно механическое травмирование слухового аппарата человека; 3- промежуточные линии «равной громкости».

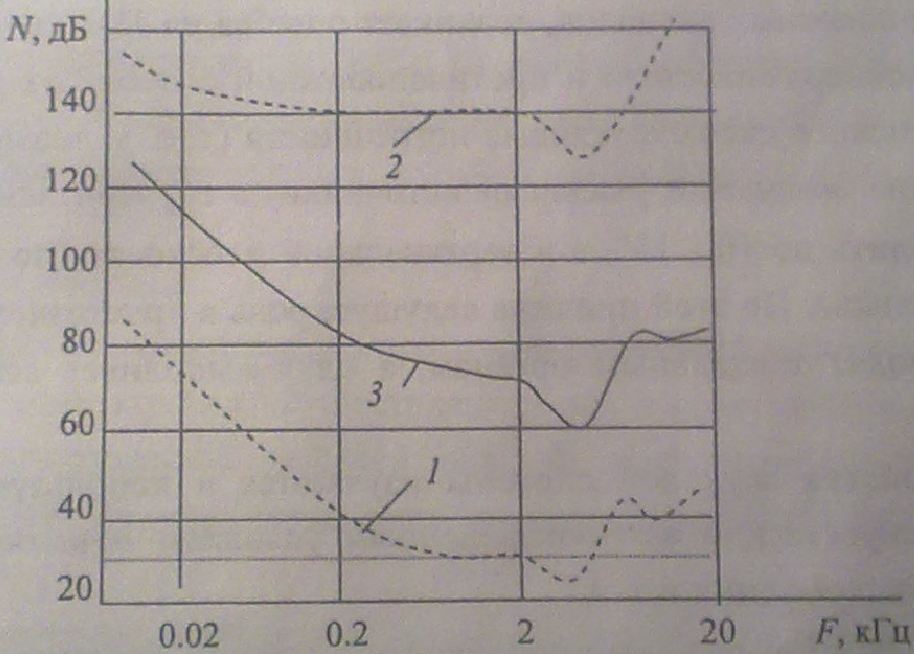
Очевидно подобие кривых, а также заметное снижение чувствительно­сти на краях частотного диапазона. Громкость L в «фонах» совпадает со слышимым уровнем громкости N в децибелах по (2.2) на частоте f = 1000

Гц: L = N _{1000 Гц}. «Провал» в области частот 3000 Гц соответствует резо­нансу объема воздушного канала слухового хода. Наряду с выделением соответствующих тональных составляющих большое практическое значение имеет возможность пространственной лока­лизации источников звуковых колебаний. Слуховые сенсоры, как и сенсоры

визуальной информации, относятся к парным сенсорам. При этом сущест­венно важными оказываются бинауральные свойства слуха по определению различий акустических сигналов, воспринимаемых правым и левым слухо­выми органами по времени прихода и амплитуде (бинауральный эффект).

Физическая основа этих различий - разновременность прихода звуко­вых волн к разным сенсорам и разные уровни сигналов, что делает возмож­ные образование «бинауральных разностей» ∆Nбин и ∆Tбин.

К бинауральным свойствам слуха относят способность определять на­правление на «кажущийся» источник звука. При этом следует различать по крайней мере две ситуации: 1)Слуховая система выполняет роль акустического пеленгатора. 2)Свойства слуховой системы изучаются и используются примени­тельно к искусственно воспроизведенным условиям объемного звука: сте­реофонии, квадрофонии и т. д. Еще слабее выражены способности слуховой системы к определению расстояния до кажущегося источника звука.

Даже при восприятии тональных сигналов возможности человеческого уха заметно ограничены. Так, в диапазоне слышимых звуков 20 Гц...20 кГц человек запоминает не более 150...200 градаций на частоте. Разница в часто­тах, свободно улавливаемая человеком, составляет ≈ 4 %. Разумеется, у от­дельных индивидуумов, обладающих «музыкальным» слухом, эти данные могут значительно отличаться. Существенно изменяются возможности уха и с возрастом человека.

Если различия по частоте и интенсивности еще сравнительно доступны для слуховых сенсоров, то определить различия по фазе человек практически не в состоянии. Это справедливо до тех пор, пока фазовый сдвиг не приведет к сдвигу по времени.

Частоты звуковых (слышимых) колебаний нахо­дятся в полосе частот от 20 до 20 000 Гц. Инфразвуковые, ультразвуковые и гиперзвуковые колебания органом слуха человека не воспринимаются. В жидкостях и газах волна распространяется только в направлении колебательного движения самих частиц среды. Такой процесс характерен для продольных волн, или волн сжатия, представляющих собой последовательность чередующихся сгущений и раз­режений частиц среды.