9. Статическая мера информации.

События можно рассматривать в виде полной группы событий .

Вообще событиями могут быть n возможных дискретных состояний, при этом выполняется соотношение .

В материальных системах неопределенность каждой ситуации характеризуется энтропией. Энтропия количественно выражается как средняя функция множества вероятностей каждого из возможных исходов опыта: . Энтропия в термодинамике означает вероятность теплового со­стояния вещества, в математике - степень неопределенности ситуации в аб­страктной задаче, в информатике она характеризует способность источника отдавать информацию.

В общем случае нужно считать, что количество информации есть уменьшение энтропии вследствие опыта. Если неопределенность снимается полностью, то информация равна энтропии: I = Н.

В случае неполного разрешения образуется частная информация, яв­ляющаяся разницей между начальной и конечной энтропией: I = Н₁- Н₂.

Наибольшее количество информации получается тогда, когда полно­стью снимается неопределенность. Если бы эта неопределенность была наи­большей - вероятности всех событий были бы одинаковы. Это соответствует максимально возможному количеству информации, оцениваемому мерой Хартли: I _Н =log₂Q = log₂1/p = -log₂p где Q - число событий, р - вероятность их реализации в условиях равноопределенности. Таким образом, I_н = Н _mах .

Абсолютная избыточность информации D_a6c представляет собой раз­ность между максимально возможным количеством информации и энтропи­ей: D_абс =1_Н- Н = Н_max- Н. Пользуются также понятием относительной из­быточности.

10. Оценка качества измерений и контроля.

Измерением называется совместимость экспериментальных и дополнительных вычислительных операций, имеющих целью определение значения измеряемой величины, выраженного в принятых единицах.

Прямые измерения – есть измерения, проводимые непосредственно над самой величиной, подлежащей оцениванию.

Косвенные измерения – есть измерения, при которых измерительные, прямые операции осуществляются над величинами, имеющими известную (аналитическую) связь с оцениваемой величиной.

Абсолютная погрешность измерения е определяется как разность меж­ду результатом измерения и действительным значением измеряемой вели­чины

х: ε = у -х.

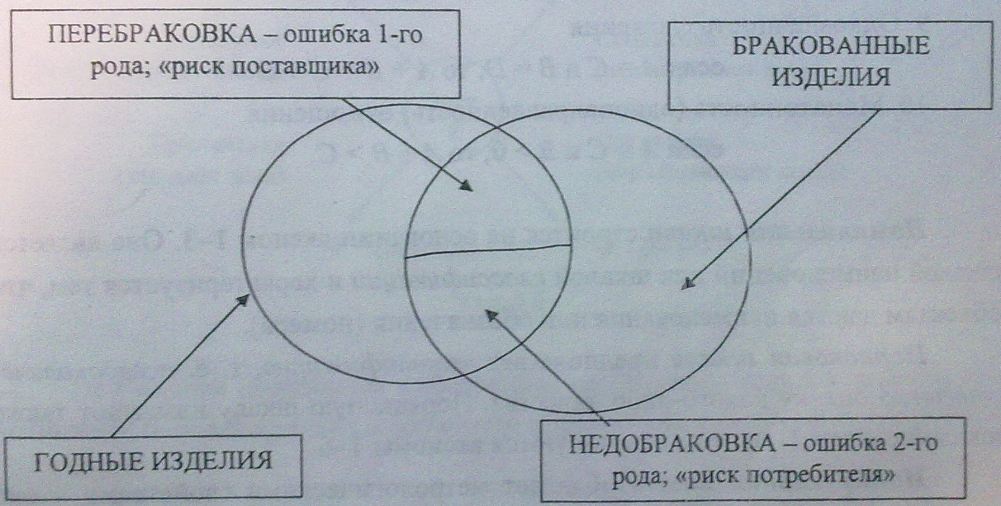
Сплошной контроль всей продукции осуществить невозможно, поэтому в производственный условиях осуществляют выборочный, статистический контроль. Принципиальным отличием операций контроля от операции измерений заключается в том, что при выборочном контроле помимо подмножеств годных и бракованных изделий, возникают два подмножества, основанные на «ошибках» двух видов: 1-го и 2-го рода.

Ошибка 1-го рода – «риск поставщика» связана с неправильной браковкой заведомо годных изделий.

Ошибка 2-го рода – «риск потребителя» связана с необоснованной приемкой заведомо бракованных изделий.

Процесс измерения можно описать как отображение множества возможных значений измеряемых величин на множество элементов шкалы измерительного устройства. Различают неметрические и метрические шкалы. К неметрическим относятся: номинальная шкала - отображение на нее есть «классификация»; порядковая шкала - отображение на нее есть «квантификация».

базисными аксиомами теории множеств:

1.Дихотомия (последовательное деление целого на две части)А = В или А ≠ В

2.Симметрия (симметричность) отношения равенстваесли А = В, то В = А

3.Транзитивность (переход) отношения равенства если А = В и В = С, то А = С

4.Необратимость (невозможность обращения одной величины) если А ≡ А, то А > А недействительно

5.Асимметричность (отношения неравенства) если А ≠ В, то А > В или А < В

6.Транзитивность отношения неравенства если A>BиB>C,тоA>C

7.Коммуникативность (переместимость слагаемых) А + В = В + А

8.Ассоциативность (независимость суммы от перемены слагаемых) (A + B) + С = A + (B+ С)

9.Однозначность сложения если А = С и В = D то А + В = С + D

10.Монотонность (однонаправленность) отношения если A = С и B > 0, то А+ В> С.

Номинальная шкала характеризуется тем, что объектам даются наименования или обозначения (номера).

Порядковая шкала предполагает квантификацию, т. е. псевдоколичественную оценку какого-либо качества.

Интервальная шкала характеризуется значениями интервала и допускает операцию арифметиче­ского сложения.

Пропорциональная шкала имеет абсолютную «нулевую» точку, вследствие чего «смещение» не допус­кается.