Перемещения и деформации

Изменение размеров и формы тела называется деформацией. Изменение линейных размеров характеризуется абсолютной линейной деформацией

∆l = l1 −l0 .

Изменение формы связано с угловой деформацией. Абсолютная деформация не характеризует механические свойства материала и зависит от первоначальных размеров тела. Поэтому вводят понятие относительной линейной деформации

=∆L1/L0*100%

Эта безразмерная величина характеризует свойство материала. Деформации бывают упругими и пластическими.

Если после снятия нагрузки тело возвращается в исходное состоя-ние, то такие деформации называют упругими.

Если после снятия нагрузки происходит изменение размеров и фор-мы, то такие деформации называют остаточными или пластическими.

Деформации не связаны с системой отсчета. Перемещения (сечений, точек) тела связывают обязательно с некоторой системой отсчета.

Перемещения могут быть линейными и угловыми.

Основные гипотезы и принципы

В сопротивлении материалов принимают следующие допущения о свойствах материалов рассчитываемых элементов конструкций:

1. Материал однороден, т.е. свойства любых сколь угодно малых его частиц совершенно тождественны.

2. Материал тела полностью заполняет весь объем тела без каких-либо пустот, т.е. тело рассматривается как сплошная среда. Допущение о сплошности можно рассматривать как следствие допущения об однород-ности материала.

3.Материал изотропен, т.е. физико-механические свойства его по всем направлениям одинаковы.

4.В известных пределах нагружения материал обладает идеальной упругостью.

5.До приложения внешней нагрузки внутренние силы (напряжения) в материале отсутствуют, т.е. не учитывают их существование вслед-ствие термообработки и других причин, их вызывающих.

В отношении характера деформаций конструкций приняты следующие допущения:

1.Перемещения точек конструкции, обусловленные ее упругими деформациями, весьма малы по сравнению с размерами элементов конструкции. Следствием этого допущения, называемого иногда принципом начальных размеров, является, в частности, возможность при составлении уравнений равновесия не учитывать изменения в расположении и направлении сил, происходящие вследствие деформации конструкции.

2.Перемещения точек элементов конструкции прямо пропорцио-нальны силам, вызвавшим эти перемещения. Конструкции, обладающие указанным свойством, называются линейно деформируемыми.

Линейно деформируемые конструкции (системы) подчиняются принципу независимости действия сил: результат от действия всех сил равен сумме результатов от действия каждой силы в отдельности и не зависит от порядка (последовательности) нагружения конструкции этими силами.

В сопротивлении материалов применяется :

1. гипотеза плоских сечений (гипотеза Бернулли): сечения плоские и нормальные к оси бруса до деформации остаются плоскими и нормальными после деформации.

2. принцип Сен-Венана. Внутренние усилия и напряжения в сечениях, достаточно удаленных от мест приложения нагрузки, не зависят от характера данной нагрузки.

Учет собственного веса бруса при растяжении и сжатии

Пусть вертикально расположенный брус постоянного сечения закреплен на верхнем конце и нагружен на нижнем свободном конце центрально приложенной силой F

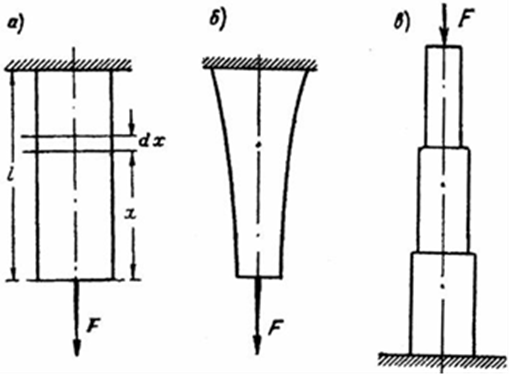
Определим напряжение в произвольном сечении бруса, расположенном на расстоянии х от оси свободного конца, принимая во внимание собственный вес бруса, причем вес единицы объема материала полагаем равным γ.

В сечении x растяжение вызывается силой F и весом нижней от се-чения части бруса, равным А⋅ γ ⋅ x. Напряжение в этом сечении составит

σ =	F + Aγx .
	A

Напряжение растет с увеличением x и достигает наибольшего значе-ния у верхнего конца

σmax =	F + Aγl	.	(2.7)
	A

Полагая σ_max =[σ], получим

A =		F	(2.8)
	[σ] − γl

Найдем удлинение бруса ∆dx = (F + γAx)dx / EA

Полагая вес всего бруса Q = Alγ, получим

∆l = _EA^Fl + ₂^Ql_EA.

Обычно влияние собственного веса в растянутых стержнях незначительно. Оно заметно сказывается лишь для очень длинных стержней. В этом случае можно сделать брус переменного сечения, подобрать такое очертание бруса, при котором во всех его сечениях напряжение будет одинаковым.

Такой брус называется брусом равного сопротивления при растяжении

На практике плавное изменение сечения заменяют ступенчатым