Вопрос 30. Методы нахождения оценок: метод моментов и метод наибольшего правдоподобия.

1.Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретич. моментов рассматриваемого распределения соответствующим эмпирич. моментам того же порядка. Дана случ. велич. Х, и ф-ция распределения известна с точностью до параметра θ (тетра). F θ (Х). Требуется оценить параметр θ. Приравниваем выборочные моменты к теоретич. моментам, и получ. оценка является состоятельной оценкой оцениваемого параметра.

Пример:

Х –случ.велич. По закону Пуассона: МХ= . Х1-число пассажиров за 1 день, х2- число пассажиров за 2-ой день. n-объём выборки; х1,х2…xn – выборка. Предлагается найти выборочное среднее, которое является выборочным начальным моментом и приравнять его матем. случ вел-ну. Таким образом случ процесс записX(t), ξ(t).

t обыч предст как время. F(x,t)=P(X(t)<x) – ф-ия распр-ия кажд сечения X(t)

Хар-ки: Мат ожидание MX(t)→m(t) ф-ия не случ, завис от t. Зав-сть случ вел-н между различ вел-ми: μ(t1,t2)=M(X(t1))-m(t1))/X(t2)-m(t2)) – корреляц момент.Чем дальше t1 от t2

тем менее зависимы случ вел-ны, тем ближе к 0 корреляц момент.

2 5. Общ. Форм-ка зад стат. Оценивания. Ген. Сов-ть и выб-ка, групп-е выб-ки.

Общая формулировка задачи статистического оценивания. Генеральная совокупность и выборка. Группирование выборки. Гистограмма частот.

Постановка задачи:

Задача статистического оценивания неизвестных параметров - одна из двух основных (наряду с задачей проверки статистических гипотез) задач математической статистики.

Предположим, что имеется параметрическое семейство распределений вероятностей   (для простоты будем рассматривать распределение случайных величин и случай одного параметра). Здесь   - числовой параметр, значение которого неизвестно. Требуется оценить его по имеющейся выборке   значений, порожденной данным распределением.

Различают два основных типа оценок: точечные оценки и доверительные интервалы.

Точечное оценивание - это вид статистического оценивания, при котором значение неизвестного параметра   приближается отдельным числом. То есть необходимо указать функцию от выборки (статистику)

,

значение которой будет рассматриваться в качестве приближения к неизвестному истинному значению  .

К общим методам построения точечных оценок параметров относятся: метод максимального правдоподобия, метод моментов, метод квантилей.

Доверительный интервал - это случайный интервал, построенный по выборке (верхняя и нижняя границы этого интервала должны быть статистиками), который содержит (накрывает) истинное значение параметра с вероятностью, не меньшей заданного значения.

Доверительные интервалы используются, когда нам нужны надежные границы, в которые попадает значение оцениваемого параметра.

Часто вместе с точечной оценкой параметра строят доверительный интервал, середина которого равна этой оценке. Его ширина является наглядной характеристикой того, насколько точна может быть данная точечная оценка.

Иногда бывает наоборот: естественным образом строится некоторый доверительный интервал, а в качестве точечной оценки параметра рассматривают его середину.

Подробнее см. статью доверительный интервал.

Генеральная совокупность – совокупность элементов, удовлетворяющих неким заданным условиям; именуется также изучаемой совокупностью.

Генеральная совокупность - все множество объектов (субъектов) исследования, из которого выбираются (могут выбираться) объекты (субъекты) для обследования (опроса).

ВЫБОРКА или выборочная совокупность — это множество объектов (субъектов), отобранных специальным образом для обследования (опроса).

Группирование выборки - группировка элементов выборки по каким-либо признакам.

Гистограмма частот - аналог функции плотности случайной величины.

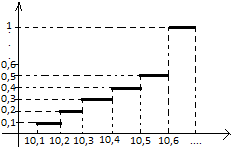F*n(x)=Mn(x)/n - выборочная функция распределения)

Гистограмма накопленных частот - график выборочной функции распределения, построенный по группированной выборке.

Выборочная функция распределения - аналог функции распределения F(x).

Эти числа можно упорядочить, группировать

31.Распределение хи-квадрат, Стьюдента и Фишера. Предположим, что есть n сл вел, нормально-распред-ых с параметрами N(0;1)

ξ 1, ξ2,… ξn;

(хи квадрат с n степенями свободы)

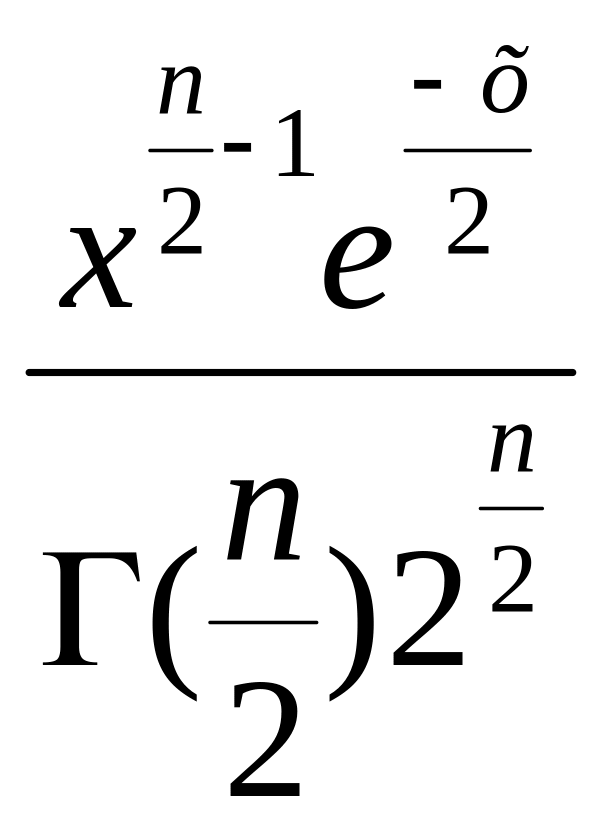- непрерывная СВ, мн-во знач-ий кот-ой лежат в (0;+∞). ф-ия плотности распределения:

f(x)= (Г-«гамма», Г(z)-гамма ф-ия);

Г(n)=(n-1)!.

М _n²=n; D_n²2n. Пусть ξ-СВ, а F(x)- ф-ия распределения. Квантилью порядка р наз-ся реш-е ур-я F(xp)=p. Распред-е Стьюдента(τ)- СВ, равная , ξ0-норм распред

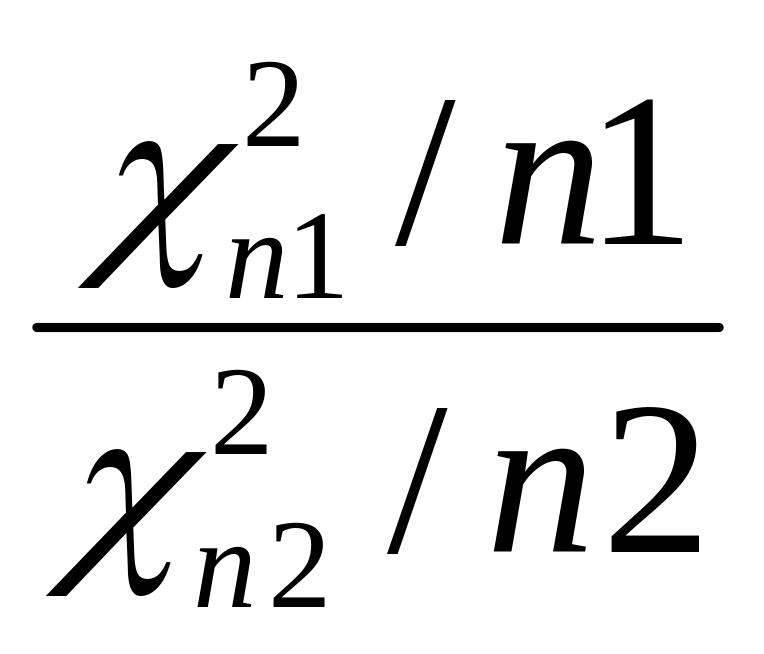~N(0;1)

Распред-е Фишера (Fn1,Fn2)=

…..(квантили найти)

33,34.Построение доверительного интервала для мат ожид-я СВ. Доверительный интервал для пар-ра θ – это такой интервал, в кот-ой попадет оцениваемый параметр с вер-тью γ. (γ-надежность доверительного интервала; [0,9; 0,95; 0,99]) выбор надежн опред-ся задачей, для кот-ой строится довер-ый интервю Пусть есть Х, х1,х2…хn- не полная инфор-ия о генер совок-ти. Полная инфор-ия – ф-ия распред, ф-ия плотности распред, таблица распределения.

М ат ожид-е – истинное знач-е измеряемой величины а. N(a,σ)~X. σ-известна (разброс результатного измерения; точность прибора, метода) а-оцениваем. Для σ есть точечная оценка - S². а,σ-неизвестны, х-выборочное среднее -эта величина имеет

распред Стьюдента с n-1 степ своб.

Где F – ф-ия распред-я Стьюдента. Ответ записывается так:

[ ], где t-квантили распред

Стьюдента, кот-ые строятся по доверительным вероятностям.