18. Сл вел, равномо распред на отрезке -

Э то непрер сл вел, для кот вер-ть попадания в люб промеж [α,β] на отрезке [а,b] пропорцион длине этого промежутка. Вер-ть того, что  попад в пром [α,β] P([α,β])=k(β-α),где k-коэф пропорциональности. Если [α,β]=[а,b],то вер-ть попадания в [а,b]=1; P([a,b])=k(b-a)=1,

Ф-ия распред сл вел имеет вид:

Если она равномерно

Распред на отрезке

Ф ункция плотности распред f(x)=F’(x)

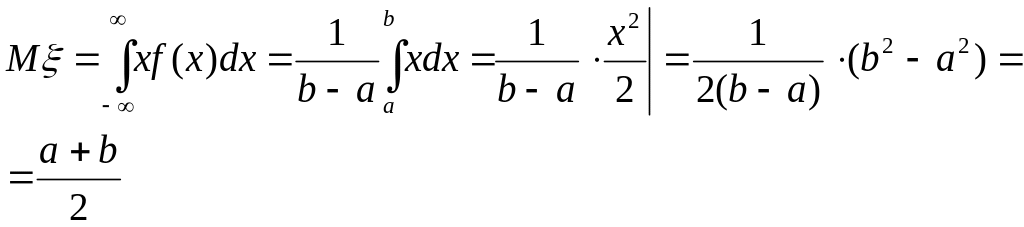
-середина отрезка [а,b]

19. сл вект и осн его хар-ки. Независ случе вел СЛ ВЕКТ-Это упорядоч набор случ вел-н ξ=(ξ1+ξ2+…+ξn). Н-р: кол-во товара на складе, стрельба по мишени (Z=(XY) отклонение точки попадания от центра по Оx и Оy). Ф-ия распред сл вектора F(x1,x2,…xn)= P(ξ1<x1,…ξn<xn)

Св-ва: 1)0<=F(x1,x2…xn)<=1. 2)

С л.вектор дискретно-распределенный, если его мн-во знач сост из изолированных точек. Дискр сл.вектор может быть задан через табл. распред

Pij=P(X=xi;Y=yj). Pij>=0

Сл.вект непрерывен, если мн-во знач заполн замкнутое мн-во с непустой внутренностью. Ф-ия плотности сл вектора:

Св-ва:

По прострRⁿ

независимые сл.в- если F(x1,x2)=F1(x1)F2(x2) или P(ξ1<x1;ξ2<x2)= P(ξ1<x1)P(ξ2<x2) или f(x1x2)=f(x1)f2(x2)

32. Теорема Стьюдента и Фишера. Распреределение Стьюдента. Расп-е случ. вел. сл. вел. U и X нез-мы, U имеет стандарт норм. расп-е N(0,1), а X – расп-е хи – квадрат с n степ. свободы. При этом n наз-ся «числ степ. свободы» расп-я Стьюдента.Расп-е Стьюдента:  — незав. стандарт норм. случ. вел., Тогда расп-е случ. вел. t, где наз-ся расп-м Стьюдента с n степенями свободы.

Пишут  . плотность расп-я , где Г — гамма-функция Эйлера. Расп-е Стьюдента симм-но.

Пример: x1…xn незав. случ. вел., .  выбор-ое ср-ее этой выб-ки, а   её выб-ую дисперсию. Тогда

Распределение Фишера –расп-е случ.вел.

где случ.вел.Х₁ и Х₂ независ. и имеют расп-я хи – квадрат с числ. степ. свободыk₁ и k₂ . k₁ – числ степ. свободы числ-ля, а k₂ – числ степ. свободы зн-ля.

Расп-е Ф. исп-т при пров-ке гипотез об адек-ти модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики.

Теорема Фишера для нормальных выборок в математической статистике —утв-е, характ-ее расп-е выб-ой дисперсии.

Пусть   — нез.вы-ка из норм. расп-я.   — выб-ое сред., а   — несмещ выб-ая дисп-я.

Случ. вел.   и   нез-мы;

Случ. вел.

20. Нер-во Чебышева. Теорема Чебышева

Пусть ξ неотр случ велич имеющ мат ожид. Тогда вер-ть того, что Р( t)M/t, t0

Пусть ξ – дискрет случ велич (т е мн-во её знач сост из изол точек) х₁, х₂…х_n-все возможн знач; p₁, p₂…p_{n –} вер-ти с кот эти знач прин

Разобьем на 2 суммы:

Т.к. все Xit = P(t) M/t

Ннер-во Чебышева: Пусть ξ случ велич имеющ мат ожид и дисперс, тогд верно ннер-во:

(1)

Док-во: рассмотр сл велич =(-М)²0

М=М(-М)²=D, t=² тогда Р(²⁾ М/²

з аменим : Р((-М)²² ) Dξ /² извлечем корень Р((-М) ) Dξ /² вер-ть больших отклон сл вел от ее среднего  ее дисперсии, деленной на ² Dξ – мера отклон СВ от её ср значПриведем ннер-во (1) к отрицанию

-вер-ть того, что кси попадет в окресность эпсилант