22 Вопрос.
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Если предел функции существует, но он не совпадает со значением функции в данной точке:
тогда точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).
Точки разрыва первого и второго рода:
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
23 Вопрос.
24 Вопрос.
Дифференциа́л (от лат. differentia — разность, различие) в математике — линейная часть приращения функции или отображения. Это понятие тесно связанное с понятием производной по направлению.
Произво́дная в математике — функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции. Физический смысл производной - скорость изменения величины или процесса.
"Приращение это в общем на сколько функция увеличилась. то есть точно. дифференциал - это то на сколько функция увеличилась, с точностью до бесконечно малых высшего порядка. то есть приближение, линейное. производная - это "скорость" увеличение дифференциала при увеличении приращения аргумента."
25 Вопрос.
Рассмотрим следующие вопросы, который касаются функций.
Если функция непрерывна, то она дифференцируема?
Если функция дифференцируема, то она непрерывна?
Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.
Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.
Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.
Найдем
производную следующей функции
.
Хорошо известно, данная функция является
непрерывной и, что ее производная будет
следующей:
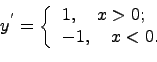
Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:
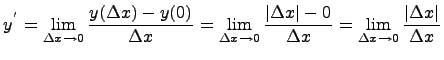
данный
предел равен 1, если
и равен (-1), если
, получаем, что предел не существует,
следовательно в нуле производной нет
и функция в нуле не дифференцируема.
Если u ( x ) ≡ const , то
u’ ( x ) ≡ 0
Если u ( x ) и v ( x ) - дифференцируемые функции в точке x0 , то:
( c u )’ = c u’ , d ( c u ) = c du , ( c – const );
( u ± v )’ = u’ ± v’ , d ( u ± v ) = du ± dv ;
( u v )’ = u’ v + u v’ , d ( u v ) = v du + u dv ;
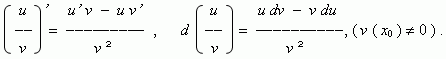
Производная сложной функции. Рассмотрим сложную функцию, аргумент которой также является функцией:
h ( x ) = g ( f ( x ) ).
Если функция f имеет производную в точке x0, а функция g имеет производную в точке f ( x0 ), то сложная функция h также имеет производную в точке x0 , вычисляемую по формуле:
h’ ( x0 ) = g’ ( f ( x0 ) ) · f’ ( x0 ) .