
- •Математика
- •1 Вопрос.
- •1. Сложение матриц.
- •2. Умножение матрицы на число.
- •3. Перемножение матриц.
- •2 Вопрос.
- •3 Вопрос.
- •4 Вопрос.
- •Миноры и алгебраические дополнения:
- •Разложение определителя по строке или столбцу:
- •5 Вопрос.
- •6 Вопрос. Системы линейных уравнений: основные определения.
- •8 Вопрос.
- •9 Вопрос.
- •10 Вопрос.
- •Переместительное свойтво:
- •11 Вопрос.
- •12 Вопрос.
- •13 Вопрос.
- •14 Вопрос.
- •15 Впорос.
- •16 Вопрос. Общее уравнение плоскости
- •Как составить уравнение плоскости?
- •Как составить уравнение плоскости по точке и двум неколлинеарным векторам?
- •17 Вопрос.
- •18 Вопрос.
- •19 Вопрос.
- •20 Вопрос.
- •21 Вопрос.
- •22 Вопрос.
- •23 Вопрос.
- •24 Вопрос.
- •25 Вопрос.
- •26 Вопрос.
- •27 Вопрос.
- •28 Вопрос.
- •29 Вопрос.
- •30 Вопрос.
- •Необходимое условие экстремума
- •Достаточное условие экстремума
- •1) Первое достаточное условие:
- •2) Второе достаточное условие
- •3) Третье достаточное условие
- •Абсолютный экстремум
- •Вопрос 31
- •Вопрос 32. Выпуклость функции и точки перегиба
- •Вопрос 33.
- •Вопрос 36. Дифференциал функции двух переменных
- •Вопрос 37. Частные производные высших порядков
- •38. Производные неявно заданной функции
- •Вопрос 39. Касательная плоскость и нормаль к поверхности
- •Примеры решения задач
- •Решение.
- •Вопрос 40.
- •Свойства градиента
- •Примеры решения задач
- •Решение.
- •Вопрос 41.
- •Вопрос 42.
19 Вопрос.
Отображение называется инъекцией, если для любых элементов x1, x2 X, для которых f(x1) = f(x2) следует, что x1 = x2. (рис. 7)
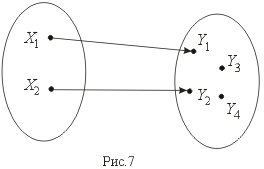
Сюръекцией (или отображением "на" ) называется отображение, при котором f(X) = Y (рис. 8).
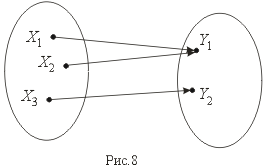
Биекция – это одновременно и сюръекция и инъекция (рис.9).
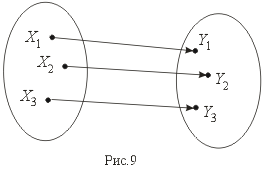
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
алгебраические:
степенная;
рациональная.
трансцендентные:
показательная и логарифмическая;
тригонометрические и обратные тригонометрические.
20 Вопрос.
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
В математике пределом последовательности элементов метрического пространства или топологического пространства называют элемент того же пространства, который обладает свойством «притягивать» элементы заданной последовательности. Пределом последовательности элементов топологического пространства является такая точка, каждая окрестность которой содержит все элементы последовательности, начиная с некоторого номера. В метрическом пространстве окрестности определяются через функцию расстояния, поэтому понятие предела формулируется на языке расстояний.
Преде́льная то́чка множества в общей топологии — это такая точка, любая проколотая окрестность которой пересекается с этим множеством.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Свойства бесконечно малых
Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если — бесконечно малая последовательность, сохраняющая знак, то — бесконечно большая последовательность.
21 Вопрос.
Предел суммы
Предел суммы равен сумме пределов, если каждый из них существует, т.е.
![]()
Предел разности
Предел разности равен разности пределов, если каждый из них существует, т.е.
![]()
Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
![]()
Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
![]()
Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.
![]()
Предел частного
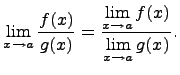 Предел
частного равен частному пределов, если
каждый из них существует и знаменатель
не обращается в нуль, т.е.
Предел
частного равен частному пределов, если
каждый из них существует и знаменатель
не обращается в нуль, т.е.
Предел степенной функции
![]()
где степень p - действительное число.
Предел показательной функции
![]()
где основание b > 0.
Предел логарифмической функции
где основание b > 0.
Теорема "о двух милиционерах"
Предположим, что для всех x близких к a, за исключением, быть может, самой точки x = a. Тогда, если
![]()
Т![]() о
о
То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу A.
