15 Впорос.
Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида:
a11x^2+ 2a12xy + a22y^2+ 2a13x + 2a23y + a33 = 0
Невырожденные кривые:
∆=/0
Вырожденные кривые:
∆=0.
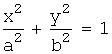ЭЛЛИПС
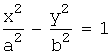ГИПЕРБОЛА
px
ПАРАБОЛА
16 Вопрос. Общее уравнение плоскости
Общее
уравнение плоскости имеет вид 
,
где коэффициенты 
одновременно
не равны нулю.
Как составить уравнение плоскости?
Конструировать уравнение плоскости будем с помощью векторов и точек. Их должно быть как можно меньше, но достаточно, чтобы однозначно определить плоскость. Одним словом, красивая математическая лаконичность. Математика – царица наук, не стерва, но строгА. А уж насколько доступна, во многом зависит от вашего к ней отношения =)
Казалось бы, плоскость можно определить с помощью двух неколлинеарных векторов. Но векторы свободны и бродят по всему пространству, поэтому ещё нужна фиксированная точка.
Как составить уравнение плоскости по точке и двум неколлинеарным векторам?
Рассмотрим
точку 
и
два неколлинеарных вектора 
.Уравнение
плоскости,
которая проходит через точку 
параллельно
векторам 
,выражается
формулой:
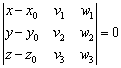
! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.
Принципиально
ситуация выглядит так:
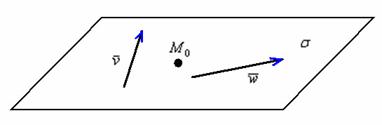Обратите
внимание, что точка и два коллинеарных вектора
не определят плоскость (векторы будут
свободно «вертеться» вокруг точки).
Пример 1
Составить
уравнение плоскости по точке 
и
векторам 
.
Решение:
Составим уравнение плоскости по точке
и двум неколлинеарным векторам:
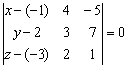
Определитель удобнее
всего раскрыть по первому столбцу:
Раскрываем
определители второго порядка:
На
первом месте у нас находится знак
«минус». Хорошим тоном считается убрать
наглеца, в этих целях меняем знак у
каждого слагаемого. Проводим дальнейшие
упрощения и получаем уравнение
плоскости:
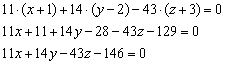
Сократить здесь ничего нельзя, поэтому:
Ответ: 
17 Вопрос.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множество
не содержащее ни одного элемента называют
пустым множеством. Его
обозначается знаком 
.
Пустое множество можно определить любым
противоречивым свойством, например
=
{х | x
х},
в области множеств оно играет как бы
роль нуля.
Множество N называется подмножеством множества М тогда и только тогда, когда каждый элемент множества N принадлежит множеству М.
а) Пересечением множеств М и N называют множество тех объектов, которые принадлежат множествам М и N одновременно.
Обозначение:
М
N
= {х|х
М
и х
N}.
б) Объединением
множеств М и N называют
множество тех элементов, которые
содержатся по крайней мере в одном из
множеств М или N. Обозначение: M
N
= {х | х
М
или х
N}.
18 Вопрос.
ограниченное множество. Множество X называется ограниченным сверху (снизу), если для всех элементов из X, существует такое число a, что x a (x a). Множество X называется ограниченным, если найдутся a и b: x X, a x b, x [a,b].
Эквивалентное определение ограниченного множества можно сформулировать следующим образом.
Определение 18. Множество X ограничено, если существует такое число c>0, что для всех x X выполнено неравенство |x| c.