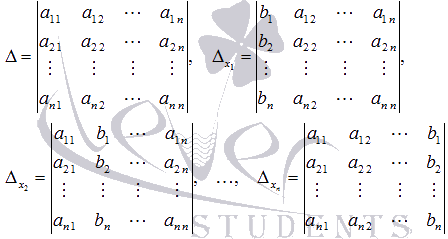Разложение определителя по строке или столбцу:
рассмотрим квадратную матрицу A n-го порядка. Выберем i,j-ый элемент этой матрицы и вычеркнем i-ую строку и j-ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом Mi j:
.
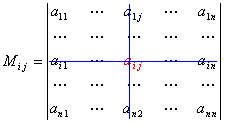Алгебраическое дополнение Ai,j элемента ai j определяется формулой
.
Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:
.
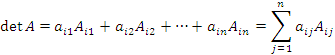Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:
.
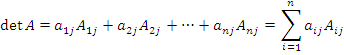Теоремы о разложении определителя имеют важное значение в теоретических исследованиях. Они устанавливают, что проблема вычисления определителя n-го порядка сводится к проблеме вычисления n определителей (n –1)-го порядка.
5 Вопрос.
Обратную
матрицу 
можно
найти по следующей формуле:
,
где 
–
определитель матрицы 
, 
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
6 Вопрос. Системы линейных уравнений: основные определения.
Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
Определение. Решение системы уравнений — это последовательность чисел (k1,k2, ..., kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1, x2, ..., xn дает верное числовое равенство.
Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
Определение: СЛАУ 1 называется совместной если существует хотя бы одно решение. Однородная система уравнений совместно потому что существует нулевое решение.
Теорема Кронекера – Капелли: Для того чтобы СЛАУ 1 была совместной необходимо и достаточно чтобы ранг матрицы при неизвестной равнялся расширенной матрице и равнялся числу ранга матрицы (r).
Замечание: Если ранг системы равен числу неизвестных то СЛАУ 1 называется определенной.
Если r<n то система называется неопределенной и тогда r неизвестных называется базисными,
оставшиеся n-r неизвестных называется свободными.
Определение: Если определитель матрицы коэффициентов системы не равен нулю то такая матрица называется невырожденной тогда СЛАУ 1 имеет решение.
Формулы
Крамера:
