Вопрос 40.

Пусть в каждой точке некоторой области   задана функция  . Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции   и обозначается   или   (читается «набла у»):  .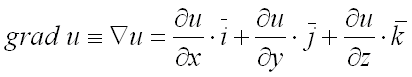

При этом говорят, что в области   определено векторное поле градиентов.

Для нахождения градиента функции   в заданной точке   используют формулу: .

 

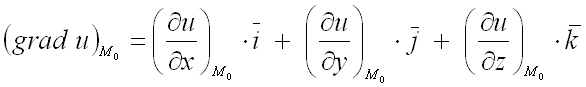Свойства градиента

1. Производная в данной точке по направлению вектора   имеет наибольшее значение, если направление вектора   совпадает с направлением градиента. Это наибольшее значение производной равно  .

2. Производная по направлению вектора, перпендикулярного к вектору  , равна нулю.

 

  

 

Примеры решения задач

Пример 1. Найти производную от функции   в точке   по направлению вектора  .

Решение.

Для решения задачи воспользуемся формулой для нахождения производной от функции   в заданной точке   по направлению вектора  : 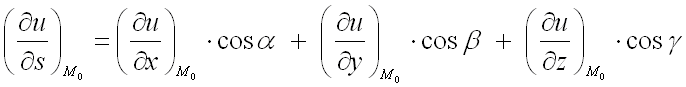, где   – направляющие косинусы вектора  , которые вычисляются по формулам: .

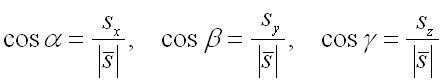По условию задачи вектор   имеет координаты  . Тогда его длина равна: .

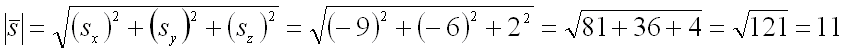Следовательно, для направляющих косинусов вектора получим следующие значения: .

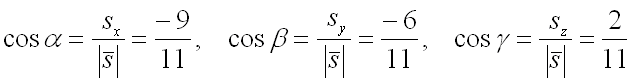Далее для решения задачи необходимо найти все частные производные первого порядка от функции  :

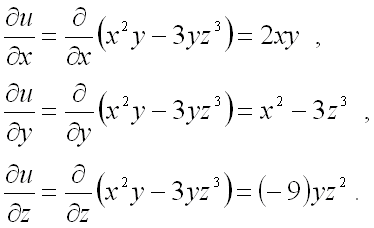
Вычислим значения этих частных производных первого порядка в точке  :

В заключении подставим полученные значения для направляющих косинусов вектора   и значения частных производных первого порядка от функции  в точке   в формулу для нахождения производной по направлению в заданной точке:

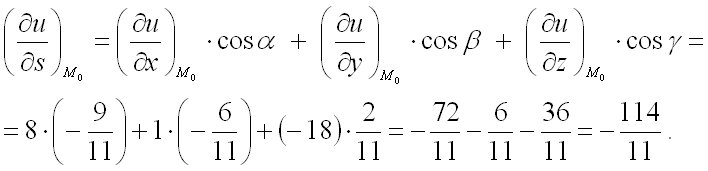
Ответ: производная от функции   в точке   по направлению вектора   равна  .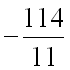

 

Вопрос 41.

Пусть в некоторой области   задана функция   и точка  . Проведем из точки   вектор  , направляющие косинусы которого  . На векторе  , на расстоянии   от его начала рассмотрим точку  , т.е.  .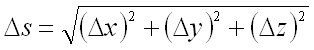

Будем предполагать, что функция   и ее частные производные первого порядка непрерывны в области  .

Предел отношения   при  называется производной от функции   в точке  по направлению вектора   и обозначается  , т.е.  .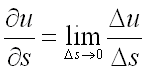

Для нахождения производной от функции  в заданной точке  по направлению вектора   используют формулу:  , где   – направляющие косинусы вектора  , которые вычисляются по формулам: .

Вопрос 42.

Линии и поверхности уровня.

Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х,у) плоскости Оху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.

Пример.

Найдем линии уровня для поверхности z = 4 — x² - y². Их уравнения имеют вид x² + y² = 4 — c  (c=const) — уравнения концентрических окружностей с центром в начале координат и с радиусами . Например, при с=0 получаем окружностьx² + y² = 4 .

Для функции трех переменных u = u (x, y, z)  уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называют поверхностью уровня.

Пример.

Для функции u = 3x + 5y — 7z —12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями 3x + 5y — 7z —12 + с = 0.