Вопрос 37. Частные производные высших порядков

Если функция f(x, y) определена в некоторой области D, то ее частные производные   и   тоже будут определены в той же области или ее части.  Будем называть эти производные частными производными первого порядка. Производные этих функций будут частными производными второго порядка.

    Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

Определение. Частные производные вида     и т.д. называются смешанными производными.

38. Производные неявно заданной функции

Пусть дана дифференцируемая функция   , для которой в некоторой точке  выполнено неравенство 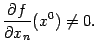  Тогда в некоторой окрестности точки   уравнение   определяет, как мы знаем из теоремы о неявной функции, некоторую функцию   , заданную вблизи точки   в   . Пусть требуется найти её частные производные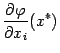  ,   . Это можно сделать, применив формулу производной сложной функции к функции   которая тождественно равна 0 в окрестности точки   ; следовательно, и все её частные производные в точке   обращаются в 0. Итак, считая параметром, от которого зависят все аргументы функции   , переменную   , где   , получаем по формуле  :   (производные  равны 0 при   ,   ), то есть   откуда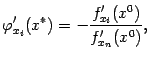 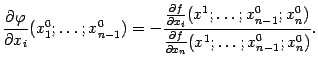    Эта важная формула позволяет вычислять производные неявно заданной функции   , не имея задающего её явного выражения.         Пример Пусть функция   задана неявно уравнением   в окрестности точки  (проверьте, что координаты этой точки удовлетворяют уравнению). Найдём производные  и   . Поскольку для функции  частные производные равны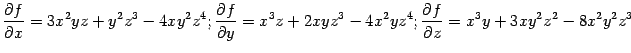 (и   так что данное уравнение действительно определяет неявную функцию), то по формуле ( 7.9 ) получаем: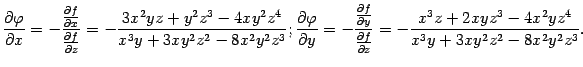 Подставляя координаты точки (1;2;1), находим: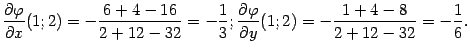      

Вопрос 39. Касательная плоскость и нормаль к поверхности

 

  

 

Пусть имеется поверхность, заданная уравнением  . Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку  , называется касательной плоскостью к поверхности в точке  .

Прямая, проведенная через точку   поверхности  , перпендикулярно к касательной плоскости называется нормалью к поверхности.

Если поверхность задана уравнением  , то уравнение касательной плоскости к этой поверхности в точке   записывается в виде: 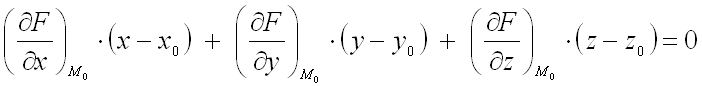, а уравнение нормали к поверхности в этой же точке – в виде: .

 

  

 

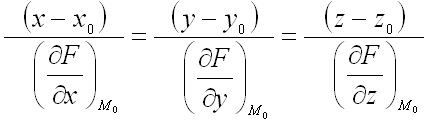Примеры решения задач

Пример 1. Найти уравнение касательной плоскости и нормали к поверхности   в точке  .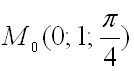

Решение.

Уравнение касательной плоскости к поверхности, заданной уравнением  , в точке   записывается в виде:  .

Так как в условии задачи уравнение поверхности задано в явном виде, то сначала его необходимо преобразовать к виду  : .

Теперь найдем частные производные 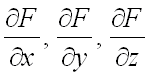  (при этом, в первых двух случаях используем правило дифференцирования сложной функции одной переменной):

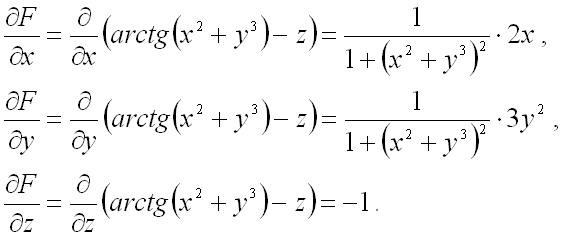
Вычислим значения частных производных первого порядка в точке  :

Подставим полученные значения в уравнение касательной плоскости:

  .
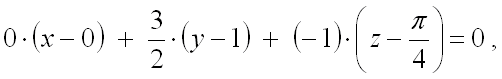
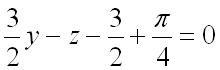