Вопрос 33.

Асимптоты

Во многих случаях построение графика функции облегчается, если предварительно построить асимптоты кривой.

Прямая называется асимптотой кривой, если расстояние от переменной точки М кривой до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви кривой.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты. Прямая x = a является вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно из условий:

или

(при этом функция f(x) может быть вообще не определена соответственно при

и

).

Замечание. Символом

о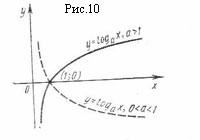 бозначается стремление x к a справа, причём x остаётся больше a, символом

стремление x к a слева, причём x остаётся меньше a.

Из сказанного следует, что вертикальные асимптоты кривой нужно искать в точках разрыва и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.

Пример . График функции y = ln x имеет вертикальную асимптоту x = 0 на границе области определения, так как

(рис. 10).

Горизонтальные асимптоты. Если

то y = b – горизонтальная асимптота кривой y = f(x) (правая при  , левая при  и двусторонняя, если пределы при  равны).

Пример . График функции

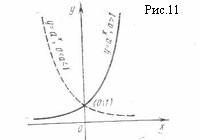
при a > 1 имеет левую горизонтальную асимпототу y = 0, так как

Правой горизонтальной асимптоты у кривой нет, поскольку

(рис. 11).

Наклонные асимптоты. Существование наклонной асимптоты определяется следующей теоремой.

Теорема. Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b, необходимо и достаточно, чтобы существовали конечные пределы

          (33)

или

      (34)

В первом случае получается правая наклонная асимптота, во втором – левая. Правая наклонная асимптота изображена на рис. 13.

П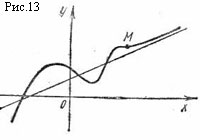 ри совпадении пределов (33) и (34) прямая y = kx + b является двусторонней асимптотой кривой.

Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).

Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0.

Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

 

Пример . Найти асимптоты графика функции

Решение. Функция определена на всей числовой прямой, кроме x = 0, т.е.

Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно,

Следовательно, x = 0 – вертикальная асимптота; при

слева

при

справа

Г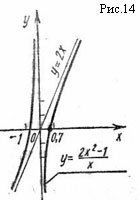 оризонтальной асимптоты кривая не имеет, так как

Выясним наличие наклонной асимптоты:

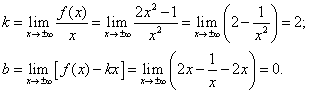
Прямая y = 2x является двусторонней наклонной асимптотой заданной кривой (рис. 14).

Вопрос 36. Дифференциал функции двух переменных

Пусть функция z = f(x,y), имеет в точке М₀(х₀,у₀) частные производные f ^/_x (х₀,у₀) и f ^/_у (х₀,у₀).

О. Полным приращением функции z = f(x,y) в точке М₀(х₀,у₀) называется разность

 

Пусть приращение функции z =f(x,y) можно представить в виде

где , то функция называется дифференцируемой в точке M ₀ (х₀,у₀).

О. Полным дифференциалом функции z=f(x,y) называется главная часть полного приращения     , линейная относительно приращений её аргументов  . Полный дифференциал функции (если он существует) равен сумме всех ее частных дифференциалов и вычисляется по формуле:

При достаточно малых (по абсолютному значению) приращениях аргументов, полное приращение функции можно с как угодно малой относительной погрешностью заменить ее полным дифференциалом. Дифференциалы dх и dy независимых аргументов функции х и у совпадают с их приращениями соответственно     . Таким образом,