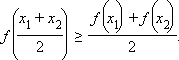2) Второе достаточное условие

     Если функция g(x) обладает второй производной  причем в некоторой точке первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка экстремум функции g(x), причем если  , то точка является максимумом; если  , то точка является минимумом.

3) Третье достаточное условие

     Пусть функция g(x) имеет в некоторой окрестности точки   N производных, причем значение первых (N - 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае:

а) Если N - четно, то точка   экстремум функции:  у функции точка максимума,    у функции точка минимума.

б) Если N - нечетно, то в точке  у функции g(x) экстремума нет.

Абсолютный экстремум

  Наибольшее(наименьшее) значение на сегменте [a;b] непрерывной функции g(x) достигается или в критической точке этой функции(т.е. где производная равна нулю или не существует), или в граничных точках а и b данного сегмента.

Вопрос 31

.Промежутки монотонности функции

Определение. Функция   называется возрастающей на множестве  , если для любых значений аргумента   из   выполняется условие  .

Теорема 1. Если функция   имеет положительную (отрицательную) производную в каждой точке промежутка  , то   возрастает (убывает) на этом промежутке.

Теорема 2. Если функция непрерывна на промежутке   и возрастает (убывает) на промежутке  , то она возрастает (убывает) и на промежутке  .

Промежутки, на которых функция   возрастает (убывает) называются промежутками монотонности функции  .

Замечание. Функция возрастающая (убывающая) на всей области определения называетсявозрастающей (убывающей) функцией.

Замечание. Функция, возрастающая (убывающая) на каждом из нескольких промежутках не обязательно убывает на их объединении.

Вопрос 32. Выпуклость функции и точки перегиба

Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x₁ и x₂ из этого отрезка 

График 3.2.3.1. Выпуклая вверх функция

Другими словами, если для любых точек x₁ и x₂ отрезка [a; b] секущая AB проходит под графиком функции f (x), то функция f выпукла вверх.

Аналогично определяется функция, выпуклая вниз.

Дважды дифференцируемая на [a; b] функция f (x) выпукла вверх, если для любого 

Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого 

Так, вторая производная функции   равна   откуда следует, что квадратичная функция выпукла вниз на всей области определения.

Пусть функция f (x) непрерывна в точке   и имеет в этой точке конечную или бесконечную производную. Тогда точка  называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.

Необходимое условие наличия точки перегиба. Если   – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то 

Достаточные условия наличия точки перегиба.

Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке   Если   меняет знак при переходе через точку   то   – точка перегиба функции f (x).

Если     то   – точка перегиба функции f (x).

 

В заключение приведем примеры, когда точка x₀ не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:

• если функция разрывна в точке   (например      );

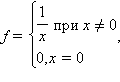
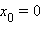• в случае угловой точки (например,    

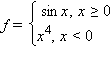
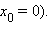
Не являются точками перегиба и точки возврата, например точка   у функции 

.