12. Цикл с подводом тепла при постоянном давлении

В 1894 г. немецкий инженер Р. Дизель теоретически разработал рабочий цикл двигателя с воспламенением от сжатия. Его именем и называется этот цикл – термодинамический цикл Дизеля.

Основные параметры данного цикла:

1) ε – степень сжатия, ;

2) – степень предварительного расширения, .

Рис. 2.4. Цикл Дизеля:

ас –адиабатное сжатие; сz – изобарный подвод теплоты; zb – адиабатное расширение; ba – изохорный отвод теплоты

Для определения термического КПД воспользуемся уравнением 1-го закона термодинамики

dQ = CpdT – Vdp. (2.23)

При р=const dQ = CpdT Q₁ = Cp (Tz - Tc). (2.24)

По аналогии с методом анализа цикла Отто получаем

Q₂ = Cv (Tв - Ta). (2.25)

Тогда термический КПД

. (2.26)

Выразим давления и температуры для цикла через исходные р_а и Т_а.

Для адиабаты ас (см. выраж. 2.6 и 2.7):

; ; (2.27)

, откуда . (2.28)

Для изобары cz:

p_{z =} p_{c =} p_{a ×} ε^k; (2.29)

, откуда . (2.30)

Для адиабаты zb

, (2.31)

, откуда . (2.32)

Подставляя полученные выражения в уравнение 2.25, получаем

. (2.33)

Из данной формулы видно:

А. Термический КПД η_t:

1. η_t повышается с увеличением степени сжатия . Это объясняется возрастанием средней температуры подводимой теплоты. В цикле Дизеля высокие показатели степени сжатия не лимитируются детонацией, как в цикле Отто. Однако по мере роста  интенсивность увеличения η_t постепенно уменьшается (рис. 2.5а);

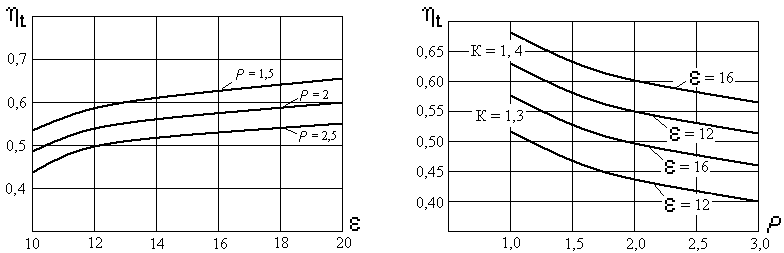
а б

Рис. 2.5. Зависимости: η_t от  и  при к = 1,35 (а);

η_t от  при различных  (б)

2. При любых значениях  термический КПД цикла Дизеля меньше термического КПД цикла Отто, т. к. множитель всегда больше единице (см. выраж. 2.17 и 2.28);

3. _t зависит от степени предварительного расширения , т. е. от нагрузки. Он уменьшается с увеличением . Это объясняется тем, что с увеличением  растёт количество теплоты, отведённой холодному источнику, а значит и уменьшается количество теплоты, превращённой в механическую работу. При увеличении  возрастает количество подведенной по изобаре теплоты Q₁, что в реальных условиях соответствует повышению нагрузки. Следовательно, максимальное значение _t достигается при минимальном количестве подведенной теплоты, что в реальных условиях имеет место при холостом ходе двигателя;

4. _t зависит от показания адиабаты к (рис. 2.5б). Это объясняется увеличением потерь теплоты и снижением среднего циклового давления;

5. При малых значениях  и значительном подводе теплоты цикл Дизеля вообще не существует, т. к.  не может превышать ;

6. Использование этого цикла в качестве прототипа рабочих процессов в реальных двигателях целесообразно только при значительных  (более 10), при работе с неполной нагрузкой (меньше ) и при значительно обеднённой смеси (приближение к к значению к воздушного цикла).

Всё, выше сказанное, свидетельствует о том, что данный цикл не используется в качестве прототипа для организации рабочего цикла в современных автомобильных двигателях.