49. Показатели тесноты связи между качественными признаками

Метод корреляционных таблиц применим не только к количественным, но и к описательным (качественным) признакам, взаимосвязи между которыми часто приходится изучать при проведении различных социологических исследований путем опросов или анкетирования. В этом случае такие таблицы называют таблицами сопряженности. Они могут иметь различную размерность. Простейшая размерность – 2х2 (таблица «четырех полей»), когда по альтернативному признаку («да» – «нет», «хорошо» – «плохо» и т.д.) выделяются 2 группы.

В корреляционном анализе недостаточно лишь выявить тем или иным методом наличие связи между исследуемыми показателями. Теснота такой связи может быть различной, поэтому весьма важно ее измерить, т.е. определить меру связи в каждом конкретном случае. В статистике для этой цели разработан ряд показателей (коэффициентов), используемых как для количественных, так и для качественных признаков.

Для измерения тесноты связи между группировочными признаками в таблицах взаимной сопряженности могут быть использованы такие показатели, как коэффициент ассоциации и контингенции (для «четырехклеточных таблиц»), а также коэффициенты взаимной сопряженности Пирсона и Чупрова (для таблиц любой размерности).

50. Прогнозирование ряда динамики с учетом сезонного фактора

К сезонным относят такие явления, которые обнаруживают в своем развитии определенные закономерности, регулярно повторяющиеся через определенные промежутки времени. Статистическое изучение сезонности ставит следующие задачи: численно выразить проявление сезонных колебаний, выявить их силу, вскрыть факторы, вызывающие сезонные колебания, выяснить экономические последствия проявления сезонности.

В статистике используются различные приемы исследования сезонных колебаний. Числовым выражением измерения сезонности являются индексы сезонности. Наиболее доступным способом исчисления индексов сезонности являются результаты сравнения средних, исчисленных по годовым данным для каждого сезонного периода (месяца или квартала), с общей средней, т.е.:

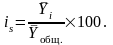
Для определения индексов сезонности широко используется способ скользящих средних. В этом случае фактические уровни (У_i) сравнивается со сглаженными средними:

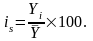
Такие индексы сезонности рассчитываются по всем сезонным периодам (допустим кварталам) каждого года, а затем на их основе определяются общие индексы сезонности, а именно:

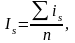
i_s – индивидуальные индексы сезонности;

n – число лет, данные которых используются в исследовании сезонности.

Если при изучении сезонных колебаний четко проступает тенденция в развитии явлений, то в подобных случаях индексы сезонности рассчитываются в результате сравнения уровней данного месяца или квартала с уровнями, исчисленными при выявлении основной тенденции для того же месяца или квартала:

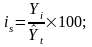общие индексы сезонности для каждого квартала вычислим:

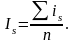
Уровни тренда данного ряда определяют методом наименьших квадратов.

Определив влияние сезонного фактора, можно найденные закономерности использовать для прогнозирования развития изучаемого процесса.

Сезонный временной ряд можно разложить на следующие компоненты:

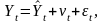
где 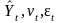- соответственно тенденция, сезонные волны, случайные колебания.

Тенденция отражает общий характер показателя за длительный промежуток времени: постоянное возрастание или убывание.