28. Дисперсия как общая мера вариации. Правило сложения дисперсий

Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные измененияпризнака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсий. Выделяют дисперсию общую, межгрупповую, внутригрупповую. Общая дисперсия измеряет вариации признака во всей совокупности под влиянием всех факторов. Пример: потребление йогурта: при выборке 100 человек

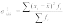Межгрупповая дисперсия характеризует систематическую вариацию, то есть различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основании группировки.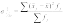 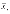- средняя по группе

Внутригрупповая дисперсия отражает случайную вариацию, то есть часть вариации, происходящую под влиянием неучтенных факторов и независящую от признака фактора, положенного в основании группировки. Данное соотношение называют правилом сложения дисперсий. 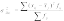x_ij – i значение признака в j группе; - среднее значение признака в j группе

f_ij – частота i-го признака в j группе

Существует правило которое связывает 3 вида дисперсии, оно называется правило сложения дисперсии.

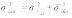
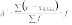- средний квадрат отклонения, взвешенный;

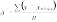- средний квадрат отклонения, невзвешенный. Согласно этому правило, общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсий, появляющейся под влиянием всех прочих факторов и дисперсий, возникающей за счетгрупп-ого признака. Зная, любые два вида дисперсий можно определить или проверить правильность расчета третьего вида.

29. Структурные средние: мода, медиана, квартиль, дециль. Смысл и применение для анализа распределений

На ряду с рассмотренными средними величинами в качестве статистических характеристик вариационных рядов распределения рассчитываются так называемые структурные средние – мода и медиана. Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.

Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины

Квартили представляют собой значение признака, делящие ранжированную совокупность на 4 равновеликие части. Различают квартиль нижний (Q₁), отделяющий ¼ часть совокупности с наименьшими значениями признака, и квартиль верхний (Q₃), отсекающий ¼ часть с наибольшими значениями признака. Это означает, что 25%процентов единиц совокупности будут меньше по величине Q₁; 25% единиц будут заключены между Q₁ и Q₂ ; 25% - между Q₂ и Q₃ и остальные 25% превосходят Q₃ .Средним квартилем Q₂ является медиана.

Кроме квартилей в вариационных рядах распределения могут определятсядецили – варианты, делящие ранжированный ряд на 10 равных частей.

Первый дециль ( d₁ ) делит совокупность в соотношении 1/10 к 9/10, второй дециль – в соотношении 2/10 к 8/10 и т.д.