18. Разрывы функций первого и второго рода. Устранимые разрывы.

Опр.1: т. Х₀ называется точкой разрыва функции f(x) , если в этой точке нарушается условие непрерывности функции.

Опр.2: т. Х₀ называется точкой устраненного разрыва функции f(x) , если в этой точке существует конечный предел функции f(x).

Опр.3: х₀ – точка разрыва первого рода функции f(x), если в этой точке существуют конечные односторонние пределы, но эти пределы не совпадают.

Опр.4: х₀ – точка разрыва второго рода функции f(x), если в этой точке не существует хотя бы один из односторонних пределов или хотя бы один равняется бесконечности.

19. Задача о мгновенной скорости движения. Механический смысл производной.

Рассмотрим прямолинейное движение некоторого тела, которое будем характеризовать материальной точкой М. Расстояние S, отсчитываемое от М_о , будет зависеть от t: S = f(t) (1)

Пусть в момент t, М находилась на расстоянии S от М_о, а в момент t+t на расстоянии S+S. То за t S изменилось на S. Отношение 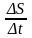дает среднюю скорость движения за t: 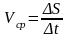(2)

t и S называются прирощениями времени и пути соответственно.

При этом, чем меньше t, тем точнее мы будет знать скорость в момент t. Наиболее точной скоростью т. М в t будет тот предел, к которому стремится V_ср при t0: 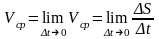(3)

Этот предел, если он существует, и называют мгновенной скоростью движения М в момент t.

Определение: Скоростью движения в данный момент (мгновенной скоростью) называется предел отношения приращения пути S к приращению времени t, когда t0.Т.к. S=f(t+t) - f(t) 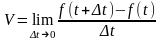 (3`)

Из (3`) следует, что V не зависит от t, а определяется только видом зависимости f(t) и моментом времени t.

1. Механический смысл первой производной.

Если S=S(t)-закон прямолинейного движения материальной точки, то производная S^/ (t) выражает значение скорости движения точки в момент времени t ( мгновенную скорость). V(t)= S^/ (t).

2. Механический смысл второй производной.

Если S=S(t)-закон прямолинейного движения материальной точки, то вторая производная S^{/ /} (t) выражает значение изменения скорости этого движения, т.е. значение ускорения будет составлять а(t)= S^{/ /} (t).

20. Математическое определение и геометрический смысл производной.

Пусть задана функция y=f(x) и пусть аргумент x получил приращение x. Тогда функция получит некоторое приращение y:

y=f(x+x) - f(x)

Составим отношение

Если предел этого соотношения существует, то его называют производной функции f(x):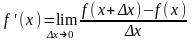

Определение: Производной функции f(x) по аргументу x называется предел отношения приращения y к приращению х, когда последнее произвольным образом стремится к нулю (0).

Геометрический смысл производной

Пусть имеется некоторая кривая y=f(x). Возьмем на ней фиксированную точку М₀ (x₀,y₀=f(x₀)) и точку М₁y=f(x). Тогда М₀М₁ - прямая, которая называется секущей. Пусть теперь М₁ М₀, но всегда М₁y. Если при неограниченном приближении М₁ к М₀ секущая М₀М₁ стремиться занять предельное положение, которое называется касательной к y в точке М₀.

Итак, пусть М₀=(x₀,y₀), а М₁=(x₀+x,y₀+y) и пусть - угол между М₀М₁ и ОХ. Тогда

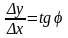
Если x0  М₀М₁, М₀М₁будет поворачиваться вокруг М₀ и  будет меняться с изменением x . Если при x0 , то прямая, проходящая через точку М₀ и составляющая с ОХ угол  и будет некоторой касательной:

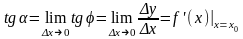 , т.е. f(x₀)=tg

Геометрический смысл: Значение производной f(x) при заданном x равно tg,  - угол, образованный касательной к графику f(x)в точке M(x,y) с положительным направлением оси ОХ..

Чтобы вывести уравнение касательной к f(x) в точке М₀=(x₀,y₀) можно поступить следующим образом. Нам известна точка, через которую она проходит, и ее угловой коэффициент, равный tg или f(x₀), т.е. k₀=f(x₀). Уравнение такой прямой имеет вид:

y-y₀=k₀(x-x₀) или y-y₀=f(x₀)(x-x₀)