
- •Числа, множества и операции над ними.
- •Функция. Основные определения и понятия .Способы её задания.
- •3.Взаимообратные и сложные функции. Сложная функция.
- •Обратная функция.
- •4.Классы элементарных функций. Основные элементарные функции.
- •5.Бесконечно малые и бесконечно большие величины и функции.
- •6. Свойства бесконечно малых величин
- •7. Свойства б.Б.В.
- •3. Произведение бесконечно большых величин есть величина бесконечно большая.
- •8. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции.
- •Определения
- •Эквивалентные величины
- •9. Бесконечные числовые последовательности. Предел последовательности.
- •Предел последовательности
- •10. Предел функции.
- •11. Теоремы о пределах.
- •12. Односторонние пределы.
- •13. Предел функции в бесконечности
- •14. Свойства непрерывных функций
- •15. Предел рациональной и дробно - рациональной функций.
- •16. Первый и второй замечательные пределы
- •17. Непрерывность функции в точке, на интервале и на отрезке.
- •18. Разрывы функций первого и второго рода. Устранимые разрывы.
- •19. Задача о мгновенной скорости движения. Механический смысл производной.
- •Механический смысл первой производной.
- •Механический смысл второй производной.
- •20. Математическое определение и геометрический смысл производной.
- •Составим отношение
- •Геометрический смысл производной
- •21. Непрерывность и дифференцируемость функций
- •22. Основные Правила дифференцирования
- •23. Производная обратной и сложной функций.
- •Доказательство. Итак
- •30. Дифференцирование неявных функций
- •31.Дифференцирование функций заданных параметрически и в полярной
- •32.Понятие о дифференциале функции и его геометрический смысл.
- •33. Производные высших порядков.
- •34.Дифференциалы высших порядков. Формула Лейбница .
- •Формула Лейбница
- •35. Теоремы Ферма, Ролля, Лагранжа и Коши. Их геометрический смысл.
- •38.Возрастание и убывание функций. Понятие об экстремуме.
- •39.Признак возрастания и убывания функции.
- •Доказательство. 1-я часть. Пусть f(X) на [a,b]. Придадим X приращение X и рассмотрим
- •40.Необходимое и достаточное условие существования экстремума.
- •41.Схема исследования функции на экстремум.
- •42. Исследование функции на экстремум с помощью второй производной.
- •Наибольшее и наименьшее значения функции на отрезке.
- •43.Формулы Тейлора и Маклорена Формула Тейлора
- •45.Исследование функций на экстремум с помощью формулы Тейлора
- •46.Выпуклость и вогнутость графика функции. Точки перегиба. Необходимое и
- •47.Асимптоты функции.
- •Горизонтальные асимптоты.
- •48.Исследование кривых, заданных параметрически (астроида, циклоида)
- •Пусть , исследуем аналогично .
- •Исследование функций, заданных в полярных координатах , можно исследовать как и параметрические, если перевести в декартовую систему координат.
- •49.0Бший план исследования функции и построения ее графика.
- •50.Касательная и нормаль к плоской кривой.
- •51.Приближенное решение уравнений. Метод Ньютона (касательных) Действительные корни .
- •52.Приближенное решение уравнений. Методы хорд, итераций и
- •54. Векторная функция скалярного аргумента и ее дифференцирование.
- •55.Свойства производной от векторной функции по скалярному аргументу.
- •56,Кривизна пространственной кривой. Сопровождающий трехгранник
- •57.Уравнения касательной, нормали, бинормали и плоскостей
- •51.Приближенное решение уравнений. Метод Ньютона (касательных) Действительные корни .
- •52.Приближенное решение уравнений. Методы хорд, итераций и
- •60.61.Интерполяция. Интерполяционный многочлен Лагранжа. Конечные разности и интерполяционная формула Ньютона
- •Интерполирующая функция Лагранжа.
38.Возрастание и убывание функций. Понятие об экстремуме.
Определение1. Функция y=f(x) называется возрастающей в промежутке (a,b), если для любых x1, x2(a,b) большему из них соответствует и большее значение функции.
x1(a,b), x2(a,b), x2>x1 f(x2)>f(x1)
Определение 2. Функция y=f(x) называется убывающей на (a,b), если для любых x1, x2(a,b) большему x соответствует меньшее значение f(x).
x1(a,b), x2(a,b), x2>x1 f(x2)<f(x1)
Значения x, при которых f(x) достигает своих наибольших или наименьших значений по сравнению с соседними, называют точками максимума и минимума.
Определение 3. x=x0 - точка максимума f(x), а f(x0) - максимум функции, если существует некоторая окрестность x0 (т.е. x0-, x0+) такая, что значение функции в любой точке x1(x0-, x0+) будет меньше, чем ее значение в x0, то есть меньше, чем максимум f(x0)
f(x0+x)<f(x0) при любом |x|<
Аналогично определяются точки максимума и минимума функции
f(x0+x)>f(x0) при любом |x|<. Точки минимума и максимума объединяются под общим названием – точки экстремума (экстремальные точки), а минимум и максимум функции – экстремумы функции.
39.Признак возрастания и убывания функции.
Теорема 1) Если f(x), дифференцируемая на отрезке [a,b], возрастает на этом отрезке, то f(x) неотрицательна на [a,b], то есть
f(x)0, x[a,b], если f(x),
2) Если f(x) непрерывна на [a,b] и дифференцируема в (a,b), причем f(x)>0, x(a,b), f(x) возрастает на [a,b].
Доказательство. 1-я часть. Пусть f(X) на [a,b]. Придадим X приращение X и рассмотрим
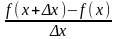 т.к.
f(x)
f(x+x)>f(x),
если x>0
т.к.
f(x)
f(x+x)>f(x),
если x>0
f(x+x)<f(x),
если x<0
Но в обоих
случаях
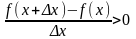 и
следовательно
и
следовательно
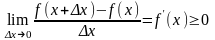 ,
что и следовало доказать.
,
что и следовало доказать.
2-я часть. Пусть f(x)>0, x(a,b). Рассмотрим x1 и x2, x1>x2, x1,x2[a,b]. По теореме Лагранжа f(x1)-f(x2)= (x1-x2). По условию теоремы f()>0, x1-x2>0 и f(x1)-f(x2)>0 f(x) возрастает.
Аналогично формулируется теорема для убывающей функции:
Теорема. Если f(x), дифференцируемая на отрезке [a,b], убывает на этом отрезке, то f(x)0 на [a,b], то есть f(x)0, x[a,b], если f(x) непрерывна на [a,b] и дифференцируема в (a,b), причем f(x)<0, x(a,b), f(x) убывает на [a,b].
Геометрический смысл. Если f(x), касательная к кривой образует острый угол с ОХ, или в некоторых точках угол =0 касательная параллельна оси ОХ, так как tg0. Если f(x), угол - тупой (или =180о в отдельных точках параллельна оси ОХ), так как tg=f(x)0.
Таким образом, теоремы позволяют судить о возрастании или убывании функций по знаку производных.
40.Необходимое и достаточное условие существования экстремума.
Экстремальные значения f(x) и расположение точек экстремума характеризуют, в некотором смысле, изменение функции в зависимости от изменения аргумента.
Теорема 1. (Необходимое условие существования экстремума).
Если f(x) дифференцируема на (a,b) и при x=x1 имеет max или min (x1(a,b)), ее производная обращается в нуль в этой точке, то есть f(x1)=0 .
Доказательство: Пусть x1 - точка максимума, …При достаточно малых x, точка x1+x независимо от знака x.(х0 заменяем везде на х1)
Пусть x>0 , переходя к пределу при x+0 получим: , как предел неположительной величины.
b) x<0
Так как для дифференцируемой в x0 функции производная слева равна производной справа f(x0)=0, теорема доказана.
Замечание. Если f(x) определена на [a,b], то она может достигать max или min только на (a,b). Так как ее поведение при x<a или x>b неизвестно.
Геометрический смысл: в точках min и max касательная параллельна ОХ.
Следствие. Если f(x) дифференцируема при любом x, то она может иметь экстремумы только в тех точках, в которых ее производная обращается в нуль. Обратное же, вообще говоря, неверно. То есть max или min не обязательно достигаются в точках, в которых f(x)=0.
функция может иметь экстремум лишь в 2-х случаях: либо в точках, где производная существует и равна 0, либо в точках, где f не существует (терпит разрыв).
Определение. Значения аргумента, при которых f(x)=0, или f(x) терпит разрыв, называются критическими точками или критическими значениями.
Поэтому для нахождения эктремумов находят все крит. точки, затем исследуют каждую из них, опираясь на теорему
Теорема 2. (Достаточные условия существования экстремума). Пусть f(x) непрерывна в некоторой окрестности критической точки x1(a,b) и дифференцируема в этой окрестности, за исключением может быть самой x1. Если при переходе слева направо через крит. т. производная меняет знак с + на -, то в x=x1 функция достигает максимального значения, если же с - на + - минимум f(x).
Таким образом, если
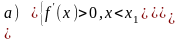
Доказательство. Пусть f(x) изменяет знак с + на -, то есть рассмотрим случай a). Применим теорему Лагранжа:
f(x)-f(x1)=f()(x-x1), где (x,x1)
1). Пусть далее x<x1. < x1, f()>0, f()(x-x1)<0 и следовательно f(x)-f(x1)<0 или f(x)<f(x1) (*)
2). x>x1. > x1, f()<0, f()(x-x1)<0 и следовательно f(x)-f(x1)<0 или f(x)<f(x1) (**)
Соотношения (*) и (**) показывают, что для любого x1(a,b) f(x)<f(x1) f(x1)=max f(x), x1(a,b).
Аналогично доказывается вторая часть теоремы о достаточном условии минимума.
Геометрический смысл. Пусть x1 достигается max f(x) x< x1, касательная к кривой образует острый угол , а при x< x1, - тупой. То есть до x1 f(x) возрастает, а после x1 f(x) убывает, таким образом в x1 происходит переход от возрастания к убыванию.
Аналогично для минимума f(x) убывает до x1, а затем возрастает.
Если же f(x3)=0, но и для x< x3 и x< x3 f(x) не изменяет знака f(x) возрастает или убывает и до и после x3 и экстремум не достигается.
