Ядерно-физические методы измерения состава вещества:
* спектроскопия резерфордовского рассеяния.
В спектре резерфордовского обратного рассеяния в кач-ве анализирующего излучения используются пучки укоренных моноэнергетических легких ионов водорода и гелия. Важнейшими факторами, определяющими разрешение метода по массам анализируемых веществ и глубине, являются энергетическое разрешение спектрометра и энергетический разброс анализирующих ионов.
* ядерный активационный микроанализ.
Это высокочувствительный неразрушающий метод кач. и колич-ого определения очень малых количеств атомов элементов в исследуемом образце. На исследуемое вещество в кач-ве возбуждающего излучения направляется поток либо нейтронов, либо высокоэнергетических заряженных частиц – ионов. Энергия заряженной частицы должна быть достаточной для того. чтобы преодолеть энергию кулоновского отталкивания ядра атома исследуемого вещества и перевести ядро в возбужденное состояние.
67.Физические основы спектроскопии резерфордовского рассеяния.
В спектроскопии резерфордовского обратного рассеяния (РОР) в качестве анализирующего излучения, направляемого на исследуемое вещество , используются пучки ускоренных моноэнергетических лёгких ионов водорода (₁Н) или гелия (₄Не). Анализирующие частицы являются ядрами (протоны и двукратно ионизированные атомы гелия);однократно ионизированные атомы гелия ведут себя в процессах ядерных столкновений также подобно ядрам. Коллимированный пучок ионов с начальной энергией направляется на образец исследуемого вещества. При этом небольшая часть падающих ионов испытывает столкновение с ядрами атомов мишени, в результате чего происходит существенное изменение энергии ионов и направления их движения. Часть падающих ионов рассеивается на угол, превышающий 90°, т.е. испытывает обратное рассеяние и может покинуть исследуемый образец.
Р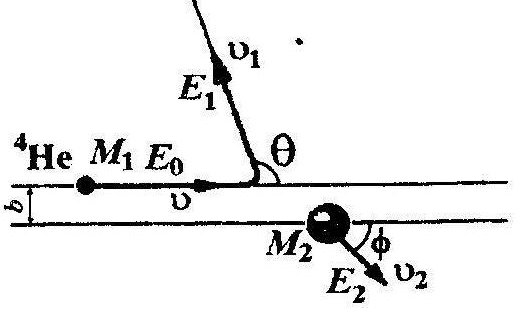
ис.
2.58. Частица массой М₁,
имеющая скорость υ и энергию Е₀
(Е₀=
М₁
υ²/2),налетает на ядро покоящегося в
выбранной системе отсчёта атома вещества
массой М₂.
После столкновения налетающая частица
и
ядро атома приобретают соответственно
скорости υ₁
и
υ₂
и энергии Е₁
и Е₂,
значения которых определяются углом
рассеяния Ѳ
и углом отдачи ф. Углы Ѳ
и ф отсчитываются от начального
направления движения налетающей частицы
и всегда принимаются положительными.
Массы ядер М₁
и М₂
измеряются в атомных единицах массы
(а.е.м.).
Законы сохранения энергии и компонентов импульса, параллельных и перпендикулярных направлению движения налетающей частицы, выражаются уравнениями
М₁υ² / 2 = М₁ υ₁² / 2 + М₂ υ₂² / 2 М₁υ = М₁ υ₁ cosѲ + М₂ υ₂ cosф 0 = М₁ υ₁ sinѲ - М₂ υ₂ sinф
Отсюда соотношение скоростей налетающей частицы:
υ₁ / υ = [ ± ( М₂² - М₁² sin²Ѳ )½ + М₁ cos Ѳ ] / [ М₂ + М₁ ]
Отношение энергий налетающей частицы в случае М₁ < М₂ определяется выражением
К = Е₁ / Е₀ = ( [ (М₂² - М₁² sin²Ѳ )½ + М₁ cos Ѳ ] / [М₂ + М₁ ] ) ²
Это отношение энергий К = Е₁ / Е₀ называют кинематическим фактором рассеяния или К – фактором . Это соотношение показывает, что энергия рассеянной частицы Е₁ определяется только массами частиц М₁ и М₂ и углом рассеяния Ѳ. Чем больше М₂ рассеивающего ядра, тем меньше потери энергии анализирующей частицы и тем больше значение К-фактора. При ↑ Ѳ К-фактор ↓ монотонно. Скорость убывания зависит от М₁ и М₂ , она растёт с ↑ М₁ и уменьшается с ↑М₂ .
Энергия рассеянной частицы зависит от массы ядра, с которым произошло столкновение, благодаря чему метод позволяет проводить анализ элементного состава вещества.
Обычно приводятся значения К-фактора при рассеянии ионов ₄Не на ядрах различных элементов в зависимости от угла рассеяния Ѳ. Различия в К-факторах рассеяния на ядрах соседних элементов достигают своих максимальных значений при углах Ѳ, близких к 180°. При изменении К-фактора изменяется и энергия рассеянных частиц Е₁ (Е₁ = К Е₀ ) . Поэтому при проведении элементного анализа методом РОР наилучшее разрешение по массам достигается при возможно больших углах Ѳ; обычно они выбираются близкими к 170° (из-за конечных размеров детектора рассеянных частиц).
68.При измерении состава вещества методом РОР на расположенный в аналитической камере исследуемый образец в условиях высокого вакуума направляется из ионного источника узкий моноэнергетический пучок анализирующих ионов. Моноэнергетичность ионного пучка достигается путём выделения из первичного пучка ионов с одинаковым удельным зарядом при отклонении в магнитном поле и последующего ускорения пучка постоянным электрическим полем. Для ускорения ионов необходимо высокое напряжение. Заряд, приносимый анализирующим пучком на образец, регистрируется интегратором тока. Измерительная информация, получаемая методом РОР, регистрируется в виде энергетического спектра обратнорассеянных ионов, где по оси абсцисс откладывается номер канала анализатора, а по оси ординат – выход обратного рассеяния в импульсах. Т.к. каждому каналу многоканального анализатора соответствует определённый небольшой интервал энергий, то спектр представляет собой распределение ионов, рассеянных на ядрах атомов исследуемого вещества, по кинетическим энергиям. Форма спектра зависит от природы анализирующих ионов, их энергии, а также от природы и состава исследуемого образца. Рис 2.60 – спектр РОР ионов ₄Не с энергией Е₀ = 3 МэВ, рассеянных под углом Ѳ = 170° на алюминиевой плёнке толщиной 400 нм, покрытой с обеих сторон золотыми маркерами. В спектре в области более низких энергий (Е ~1,5 МэВ) имеет пик, соответствующий рассеянию ионов гелия на ядрах атомов Al. Значение К – фактора для Al равно 0,5525, и ионам ₄Не , рассеянным на ядрах атомов Al, расположенных на поверхности анализируемого образца, соответствует энергия Е= 1,6575 МэВ . На спектре эта энергия обозначена вертикальной стрелкой. Ионы ₄Не с меньшей энергией, формирующие обсуждаемый спектральный пик, рассеяны на ядрах более глубоких атомов алюминиевой плёнки. Толщину плёнки можно определить по полуширине спектрального пика на половине высоты ∆ЕAl . Ионам гелия, рассеянным на ядрах поверхностных атомов золота, соответствует энергия Е= 2,7675 МэВ ( К Au = 0,9225) , поэтому спектральные пики , формируемые ионами ₄Не , рассеянными на золоте , расположены в области более высоких энергий. Правый спектральный пик Au ₁ соответствует ионам ₄Не , рассеянным на правом маркере, обращённом к налетающим ионам гелия , а левый пик Au ₂ - ионам гелия, рассеянным на левом маркере и потерявшим часть энергии при прохождении алюминиевой плёнки туда и обратно. Рис 2.61 – спектры РОР ионов ₄Не от поверхности кремния с нанесённой плёнкой никеля. В случае чёткой границы между плёнкой и кремниевой подложкой ( рис. а ) имеют место спектральные пики, соответствующие рассеянию анализирующих частиц на кремнии и никеле. Т.к. масса атомов никеля больше массы атомов кремния, то при рассеянии на ядрах атомов никеля энергетические потери ионов гелия меньше; этому соответствует большее значение К-фактора, и спектральному пику, обусловленному рассеянием ни никеле, соответствуют большие энергии. В отсутствие плёнки сигнал, обусловленный рассеянием анализирующих ионов на ядрах атомов массивной ( толстой) кремниевой подложки, простирался бы на интервал энергий Е ≤ КSi Е₀ . Но т.к. кремниевая подложка находится под плёнкой никеля и атомы кремния не выходят на поверхность , то сигнал от подложки расположен при энергиях намного меньше значения КSi Е₀. Сигналу от тонкой плёнки никеля соответствует определённый небольшой энергетический интервал ∆Е, расположенный при Е ≤ КNi Е₀. В результате термообработки из-за взаимной диффузии атомов никеля и кремния в приповерхностной области формируется силицид никеля Ni₂Si. В спектре (рис. б) на сигнале от кремния появляется ступенька АSi, соответствующая наличию кремния в слое силицида; при этом атомы кремния , входящие в состав силицида металла , выходят на поверхность исследуемого образца. Ширина сигнала от никеля ∆ЕNi несколько увеличивается из-за уширения никельсодержащего слоя . Порядок обработки спектров РОР.
Калибровка энергетической шкалы анализатора. При этом осуществляется переход от шкалы «№ канала анализатора» по оси абсцисс к шкале «энергия». По соответствующим таблицам определяются значения К-фактора для обоих элементов при заданном угле рассеяния и рассчитываются энергии, соответствующие этим каналам Еi = Кi Е₀ После этого рассчитывается энергетическая ширина канала, измеряемая в кэВ/канал δЕ = ( Е₂ - Е₁) / (n₂ - n₁) , где n₁ и n₂ - номера каналов, соответствующие положению сигналов от поверхности. С использованием вычисленного значения δЕ и табличных значений К-факторов по соответствующим спектральным пикам определяются другие элементы, входящие в состав анализируемого слоя мишени. Энергии и номера каналов анализатора, соответствующие анализирующим ионам, претерпевшим упругое рассеяние на ядрах атомов, расположенных на поверхности, наносятся на спектр. 2)Построение шкалы глубин ( определение толщины δt, соответствующей одному каналу анализатора, и нанесение полученного масштаба на ось энергии) для каждого из элементов. Причём шкалы глубин для основного материала ( матрицы) и каждой из примесей могут существенно различаться. Для построения шкалы глубин с использованием табличных значений сечений торможения ε рассчитывается фактор тормозного сечения [ε] ' j [ε] ' j = [ [ К j /cos Ѳ₁] * εi (Ε₀ ) + [ 1/ cos Ѳ ₂] * εi ( К j Ε₀ ) ], где индекс i относится к тормозящей среде – основному материалу, а индекс j – к рассеивающему центру – ядру атома примеси. ε = эВ / (ат. / см²). Определяется также толщина δt поверхностного слоя, соответствующая одному каналу анализатора δt = δЕ / ( N [ε] ' j ),где N – атомная плотность основного материала исследуемого образца. δt = нм/канал. Высота спектра РОР от отдельного элемента на определённом участке определяется соотношением . Нi = q Ω σi Ni δt ,где q – количество (заряд) направляемых на образец анализирующих ионов; Ω – телесный угол захвата детектора ; σi – дифференциальное сечение рассеяния анализирующих ионов на ядрах i-го элемента ; Ni δt - количество атомов элемента в слое образца толщиной δt. Тогда высота сигнала от мишени Нi = q Ω σi δЕ / [ε] 'i и примеси Нj = q Ω σj ( Nj δЕ) / ( N i [ε] 'j ) ,где N i и Nj - концентрации соответственно атомов мишени и примеси в слое δt. Отношение высоты сигнала примеси к высоте сигнала матрицы Нj / Нi = ( σj Nj δЕ [ε] 'i ) / (σi N i δЕ [ε] 'j ) = ( σj Nj [ε] 'i ) / (σi N i [ε] 'j ) . Отсюда отношение концентраций элементов Nj / N i = ( σi [ε] 'j Нj) / (σj [ε] 'i Нi) . Так определяется относительная концентрация примеси, а также рассчитывается профиль распределения примеси, который проводится пошагово, начиная от уровня поверхности. Вначале строят шкалы глубин для матрицы и примеси. Затем вычисляется отношение концентрации элементов в слое δt вблизи поверхности мишени. Далее расчёт отношения концентраций проводится с определённым шагом по глубине. При этом высоты сигналов от примеси и матрицы берутся на одинаковой глубине исследуемого образца. 3)Определение интегрального количества атомов примеси в исследуемом веществе осуществляется по площади Аj под спектральным пиком примеси. Просуммировав все отсчёты ( в импульсах ) под пиком примеси, получаем Аj = q Ω σj Nj t = q Ω σj ( Nt )j ,где ( Nt )j - интегральное количество примеси в анализируемом слое ( слоевое содержание примеси) , измеряемое в атом/см². Сопоставляя площадь под пиком примеси Аj и высоту сигнала матрицы Нi , получим ( Nt )j = ( Аj σi δЕ ) / ( Нi σj [ε] 'i ). При определении Аj под спектральным пиком той или иной примеси нужно провести вычитание фона. Таким образом, метод РОР позволяет измерять элементный состав материалов, концентрацию элементов в приповерхностном слое, их стехиометрию, распределение элементов по глубине и т.д.
6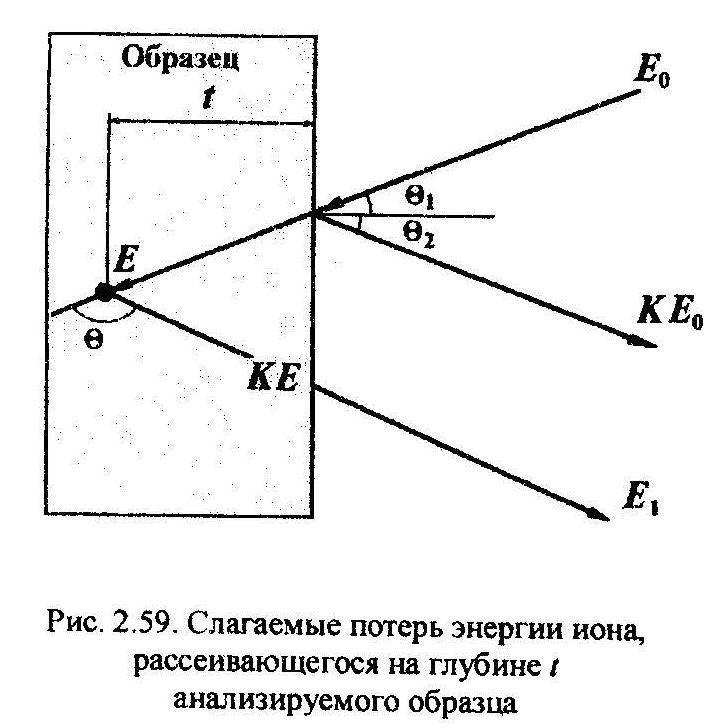
9.
В
спектроскопии резерфордовского обратного
рассеяния (РОР) в качестве анализирующего
излучения, направляемого на исследуемое
вещество , используются пучки ускоренных
моноэнергетических лёгких ионов водорода
(₁Н)
или гелия (₄Не).
Анализирующие частицы являются ядрами
(протоны и двукратно ионизированные
атомы гелия);однократно ионизированные
атомы
гелия ведут себя в процессах ядерных
столкновений также подобно ядрам.
Коллимированный пучок ионов с начальной
энергией направляется на образец
исследуемого вещества. При этом небольшая
часть падающих ионов испытывает
столкновение с ядрами атомов мишени, в
результате чего происходит существенное
изменение энергии ионов и направления
их движения. Часть падающих ионов
рассеивается на угол, превышающий 90°,
т.е. испытывает обратное рассеяние и
может покинуть исследуемый образец.Поскольку
вероятность рассеяния анализирующих
ионов на ядрах атомов весьма мала, то
большинство из них проникает на глубину
до тысяч атомных слоёв, прежде чем
произойдёт ядерное столкновение. При
этом энергия ионов расходуется на
возбуждение электронной подсистемы
мишени. Величина , на которую регистрируемая
энергия рассеянных частиц меньше
максимально возможной, соответствующей
столкновениям на поверхности, зависит
от пути, пройденного ионом в мишени.
Рис 2.59 – слагаемые потерь энергии для частицы, рассеивающейся на ядре атома, расположенного на некоторой глубине t. Они включают потери энергии в результате электронного торможения на пути входа в вещество:
∆Е вх = ( dE/ dx) *( t / cos Ѳ₁ ),где Ѳ₁ - угол падения анализирующих ионов на поверхность образца; (dE/ dx) – потери энергии на единице пути иона. Тогда энергия иона на глубине t , Еt = Е₀ - ∆Е вх.Затем часть энергии иона теряется при упругом рассеянии на ядре атома мишени ∆Е s = (1-К) Еt. В результате электронного торможения на пути выхода иона из вещества имеют место потери энергии ∆Е вых = ( dE/ dx)’ * ( t / cos Ѳ₂ ),где Ѳ₂ - угол между нормалью к поверхности образца и направлением на детектор; (dE/dx)’ – потери энергии на единице пути иона. Конечная энергия частицы : Е₁ = Е₀ - ∆Е вх - ∆Е s - ∆Е вых
Разность энергий ионов , рассеянных на поверхности и на глубине t
∆Е = К Е₀ - Е₁ = [ (К / cos Ѳ₁) * ( dE/ dx) + ( 1/ cos Ѳ₂ )* (dE/ dx)’] * t
Потери энергии анализирующих ионов нелинейно зависят от энергии, но, в случае если относительные потери энергии невелики, можно считать их постоянными и равными потерям при Е вх и Е вых соответственно. dE / dx = эВ/Å или эВ/ нм. Из-за энергетических потерь метод является чувствительным к глубине, на которой находятся атомы того или иного элемента.