11. Характер и параметры задержки сигнала измерительным преоб­разователем определяют, как правило, экспериментальным пу­тем. При этом на вход измерительного преобразователя воздействуют известным тестовым сигналом x_e(t), который определенным образом изменяется во времени, и наблюдают соответствующее изменение выходного сигнала x_a(t), или отклик.

Задержку отклика измерительного преобразователя во времени можно описать соответствующим уравнением, отображающим функ­циональную зависимость выходной величины х_а от входной х_е: x_a(t) = K_px_e(t), где К_р - коэффициент преобразования. (1.20)

При наличии временных задержек выходной величины относи­тельно соответствующих изменений входной величины в уравнении (1.20) появляются члены, содержащие производные выходной вел-ны x_a(t) по врем. Наивысший порядок производной опред-ся порядком задержки. Напр, ур-ние, опис-щее изме­рит преобразователь с задержкой первого порядка, имеет вид Суммируемые в левой части ур-ия выражения должны иметь одинак размерности. Поэтому след-но dima₀ =1, dima₁ = T. Величину a₁, называют постоянной времени и обозначают Т, а a₀=1.

Тогда дифференциальное уравнение для измерительного преобра­зователя с задержкой первого порядка . Решением этого диф ур-ия является ф-ия 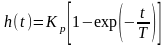. Ф-ия опис временную задержку отклика измерит-го преобразователя на скачкообразный тестовый сигнал и назыв-ся переходной ф-ей преобразователя с задержкой первого порядка.

М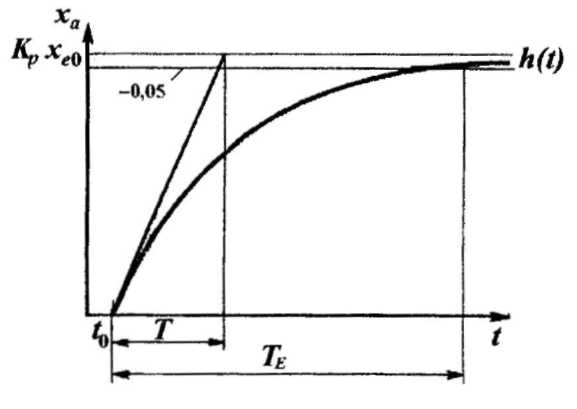 ногие величины можно изменять скачкообразно и использовать эти скачки в качестве тестовых сигналов при определении времени задержки измерительного преобразователя. Для обеспечения единого подхода независимо от вида изменяющейся величины выбирают ее значение, =1, и такой скачок называют единичным. Реакцию преобра­зователя на такой единичный ска­чок называют пе­реходной функ­цией h(t) измери­тельного преобразо­вателя, которая вы­ражается аналитиче­ски (при использовании в качестве тестового сигнала единично­го скачка принима­ется К_р=1).

Это график переходной функции для измерительного преобразователя с задержкой перво­го порядка, переходный процесс в котором является апериодиче­ским. Т. к. теоретич выходная величина достигает своего дей­ствительного значения за бесконечно большой интервал времени, то для характеристики процесса установления действит-го значения величины Хао = КрХео определяют время установления T_e=T₉₅, за которое эта величина достигает определенного уровня, обычно 95% от устанавливающегося действительного значения. Абсцисса точки пересечения касательной к графику функции в точке, соответствующей моменту времени t_o, с линией х_а определяет постоянную времени Т.

Поскольку при t=3T exp(-t/T)=ехр(-З)≈0,05, т. е. h(t) отли­чается от значения, равного единице, с отклонением ±5%, то время установления T_E≈ ЗТ.

К моменту, равному постоянной времени (при t = T), переходная ф-ия

h(t)= К_p[1-ехр(-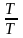 )] = К_р[1-ехр(-1)] = 0,632К_р

и выходная величина приним значение, = 63,2% от ее уста­навливающегося действит значения.

Откликом на очень короткий (∆t→0) интенсивный (амплитуда А → ) тестовый сигнал (единичный импульс), который модулирует­ся δ-функцией Дирака , является импульсная переходная, или весовая, функция g(t). Импульсная переходная функция g(t) получается дифференцировани­ем по времени переходной функции h(t):

. График этой функции также представлен на соответствующем ри­сунке. Постоянная времени Т определяется с применением касательной к графику функции в точке t = 0.

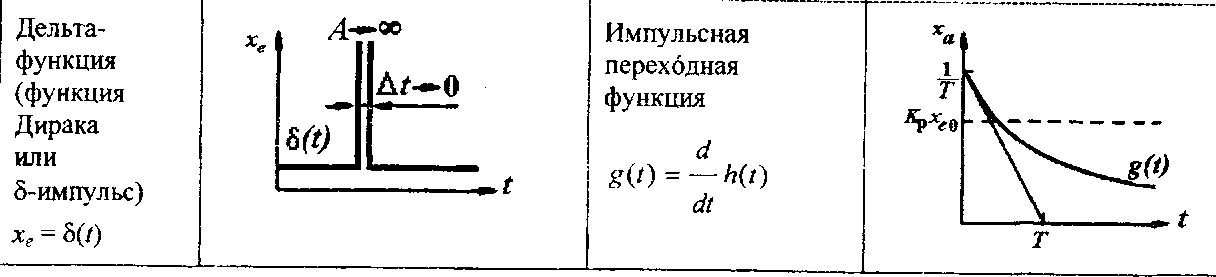
12. Характер и параметры задержки сигнала измерительным преоб­разователем определяют, как правило, экспериментальным пу­тем. При этом на вход измерительного преобразователя воздействуют известным тестовым сигналом x_e(t), который определенным образом изменяется во времени, и наблюдают соответствующее изменение выходного сигнала x_a(t), или отклик.

Задержку отклика измерительного преобразователя во времени можно описать соответствующим уравнением, отображающим функ­циональную зависимость выходной величины х_а от входной х_е: x_a(t) = K_px_e(t), где К_р - коэффициент преобразования. (1.20)

При наличии временных задержек выходной величины относи­тельно соответствующих изменений входной величины в уравнении (1.20) появляются члены, содержащие производные выходной вел-ны x_a(t) по врем. Наивысший порядок производной опред-ся порядком задержки.

Напр, ур-ние, описывающее изме­рит преобразователь с задержкой втор порядка, имеет вид

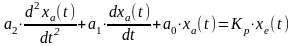(!) Суммируемые в левой части ур-ия выражения должны иметь одинаковые размерности. Поэтому а . Отсюда следует, что dima₀ =1, dima₁ = T, dima₂=T². Величину a₁, называют постоянной времени и обозначают Т. Аналогично, величину a₂, называемую постоянной времени второго поряд­ка, можно обозначить Т². И, следовательно, в этих обозначениях a₀=1.

Тогда дифференциальное уравнение для измерительного преобра­зователя с задержкой второго порядка можно записать в виде

. Решением диф ур-ния явл-ся ф-ия 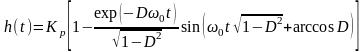, где D - коэффициент затухания, (D=T₁/T₂²=(T₁/T₂) , T₂=1/ω₀), где ω₀ – собств-я циклич частота незатух-их колебаний измерит цепи. Эта ф-ия описывает временную задержку отклика измерительного преобразователя на скачкообразный тестовый сигнал и называются переходной функцией преобразователя с задержкой второго порядка.

Затухающие колебания совершаются под действием возвращающей квазиупругой силы F_возвр=-kx и затухают при наличии силы сопротивления среды F_conp=-bυ. Уравнение дина­мики движения системы: -kx- bυ=ma, где m - масса системы; а - ускорение ее движения; υ - скорость; х - смещение от положения равновесия (координата); b - коэффициент сопротивления среды; k - коэффициент упругости (пропорционально­сти между смещением х и значением возвращающей силы).

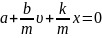ma + bυ + kx = 0 или (**) → или (*)

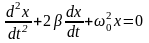где является циклической частотой собственных колебаний системы; β=b/2m называется коэффициентом затухания колебаний. Выражение (*) -дифференциальное уравнение затухающих колебаний.

Левые части выражений (**), (*) и (!), с учетом соотноше­ний m=Т₂², b=2Т₁ и k=1, аналогичны. Из их сопоставления получаем следующие выражения для коэф­фициента затухания и частоты собственных колебаний измерительной цепи: β→D=T₁/T₂², и соотношения T₂=1/ω₀ и . Выражения (1.32) и (1.33) позволяют выразить коэффициент зату­хания (демпфирования) D и собственную частоту через постоян­ные времени T₁ и Т₂, которые, в свою очередь, могут быть определены экспериментально с применением тестовых сигналов и анализа от­кликов на них.

Г рафик переходной функции h(t) для преобразователей с задержкой второго по­рядка, с затухающим колебательным переходным процессом и за­паздыванием представлен на рис. 1.7. Время запаздывания сиг­нала Т_т представляет собой интервал от момента t₀ начала действия единичного скачка до появления воспринимаемого значения отклика, что зависит от порогов чувствительности испытуемого преобразова­теля и регистрирующего устройства. Время задержки колебаний Т_v определяется по точке пересечения с осью абсцисс касательной в точке w перегиба графика. Время установления колебаний Т_А определяется моментом времени пересечения касательной в точке w с действительным значением х_а0 = К_рх_е0. Период колебаний средства измерения равен Т_р. В качестве времени установления средства измерения Т_Е принимается интервал времени, по истечении которо­го выходная величина в затухающем колебательном переходном про­цессе перестает выходить за границы, превышающие ±0,05 (±5%) действительного значения х_а0 = К_рх_е0.

13.При использовании периодического синусоидального сигнала в качестве тестового откликом является также синусоидальный сигнал с временной задержкой. Частота обоих сигналов - входного и выходного - остается одной и той же, но их амплитуды различны, и имеется фазовый сдвиг (рис. 1.8). Отношение амплитуд выходного и входного сигналов и сдвиг фаз δφзависят от частоты испытательного сигнала: х_а0/х_е0 =f₁(ω) иδφ= f₂(ω).

Э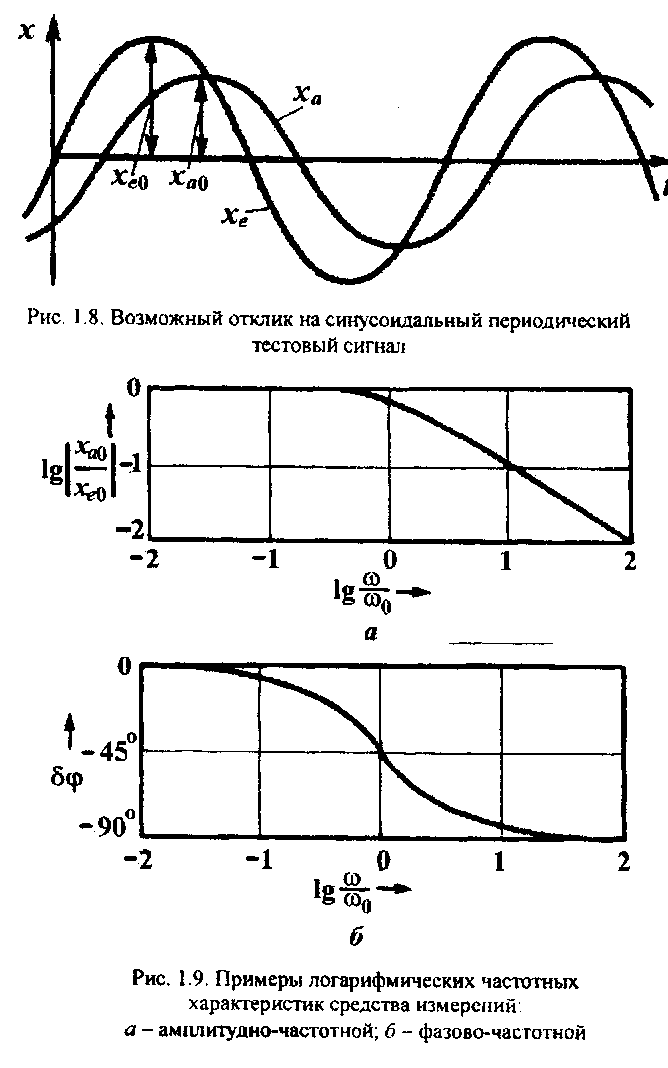 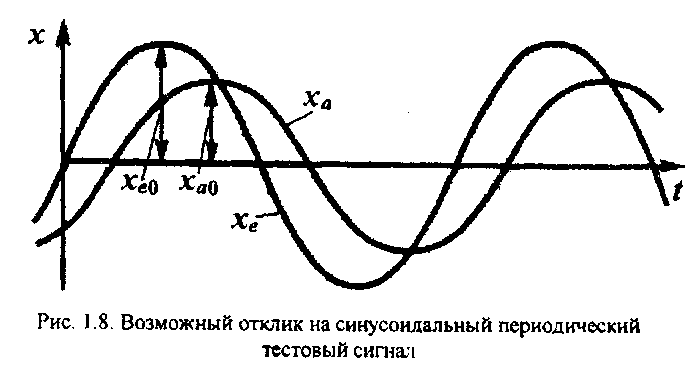ти зависимости используются в качестве динамических частотных характеристик измерительных преобразовате­лей и средств измерений. Часто динамические характеристики представляют графически в логарифмическом масштабе в зависи­мости от lg(ω/ω₀) (где ω₀ ^_ собственная частота колебаний средства измерения): амплитудно-частотная характеристика - зависимость lg от lg(ω/ω₀) и фазово-частотная характеристика - зависимость δφ от lg(ω/ω₀). Примеры таких характеристик приведены на рис. 1.9.

Частотные характеристики - амплитудно-частотная и фазово-частотная - в совокупности образуют комплексный коэффици­ент передачи G(iω), равный отношению комплексных выходной и входной величин:

где модуль отношения действительных амплитуд в зависимости от частоты ω

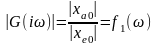есть амплитудно-частотная характеристика, а зависимость аргумента этой функции от частоты δφ(ω) =f₂(ω) - фазово-частотная характери­стика.

К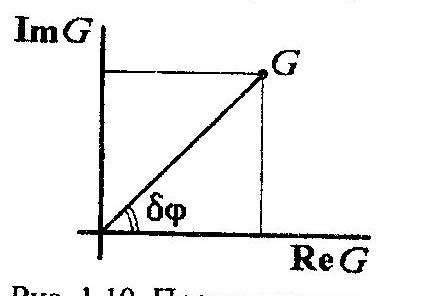 омплексный коэффициент передачи G( ) можно представить как в тригоно­метрической, так и в обычной форме: G( ) = ReG + i*ImG, и изобразить графически на комплексной плоскости. При этом модуль компл коэф передачи: 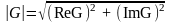, а сдвиг фаз: .

8.Если же входная измеряемая величина изменяется во времени х_е = x_e(t), то имеет место соответствующее изменение выходной вели­чины x_a(t) и измерение осуществляется в динамическом режиме. Ре­жим измерений, результатом которого является функциональная зависимость выходной величины от времени, т. е. когда выходной сигнал средства измерения изменяется во времени в соответствии с изменением входной измеряемой величины, называется динами­ческим. Динамические параметры и характеристики измеритель­ных преобразователей отражают реакцию преобразователей на изме­нения во времени входных воздействий.

Динамические характеристики средств измерений под­разделяются на:

Полные:

• переходная и импульсная переходная характеристики;

• амплитудно-частотная и фазово-частотная характеристики;

• комплексный коэффициент передачи, представляющий собой совокупность амплитудно-частотной и фазово-частотной характеристик;

• передаточная функция.

Частные динамические характеристики относят лю­бые функционалы или параметры полных динамических характери­стик:

времена задержки: время установ­ления, время успокоения, время запаздывания, а также по­рядок задержки, постоянная времени и др.

Динамические характеристики средств измерений можно также подразделить на: временные и частотные. К полным временным характеристикам относятся переходная и импульсная перехо­дная; к полным частотным - амплитудно-частотная и фазово-частотная характеристики, а также комплексный коэффициент передачи и передаточная функция.

9. Характер и параметры задержки сигнала измерительным преоб­разователем определяют, как правило, экспериментальным пу­тем. При этом на вход измерительного преобразователя воздействуют известным тестовым сигналом x_e(t), который определенным образом изменяется во времени, и наблюдают соответствующее изменение выходного сигнала x_a(f), или отклик.

Задержку отклика измерительного преобразователя во времени можно описать соответствующим уравнением, отображающим функ­циональную зависимость выходной величины х_а от входной х_е:

x_a(t) = K_px_e(t),где К_р - коэффициент преобразования.

При наличии временных задержек выходной величины относи­тельно соответствующих изменений входной величины в уравнении появляются члены, содержащие производные выходной вели­чины x_a(t) по времени. Наивысший порядок производной определяет­ся порядком задержки. Например, уравнение, описывающее изме­рительный преобразователь с задержкой второго порядка, имеет вид

Суммируемые в левой части уравнения выражения должны иметь одинаковые размерности. Поэтому

Отсюда следует, что dim a₀ = 1, dim a₁= T, dim a₂ = Т². Величину а ₁, называют постоянной времени и обозначают Т. Аналогично, величину а₂, называемую постоянной времени второго поряд­ка, можно обозначить Т². И, следовательно, в этих обозначениях а₀= 1.

Тогда дифференциальное уравнение для измерительного преобра­зователя с задержкой второго порядка можно записать в виде

, а для преобразователя с задержкой первого порядка

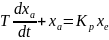
Так как теоретически выходная величина достигает своего дей­ствительного значения за бесконечно большой интервал времени, то для характеристики процесса установления действительного значения величины х_а0 = КрХ_е0 определяют время установления Т_Е = Т₉₅, за которое эта величина достигает определенного уровня, обычно 95% от устанавливающегося действительного значения.

А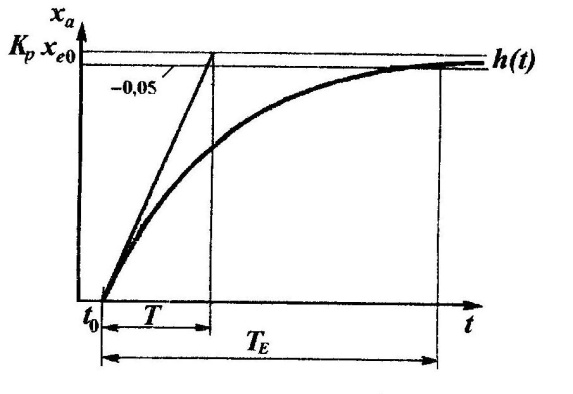 бсцисса точки пересечения касательной к графику функции в точке, соответствующей моменту времени to, с линией х„ определяет постоянную времени Т.

Поскольку при t = ЗТ ехр(-t/T) = ехр(-З) ≈0,05, т. е. h(t) отли­чается от значения, равного единице, с отклонением +5%, то время установления T≈ ЗT.К моменту, равному постоянной времени (при t = Т), переходная функция h(t) = К_р[1- ехр(- )] = К_р[1 - ехр(-1)] = 0,632 К_р, и выходная величина принимает значение, равное 63,2% от ее уста­навливающегося действительного значения.

В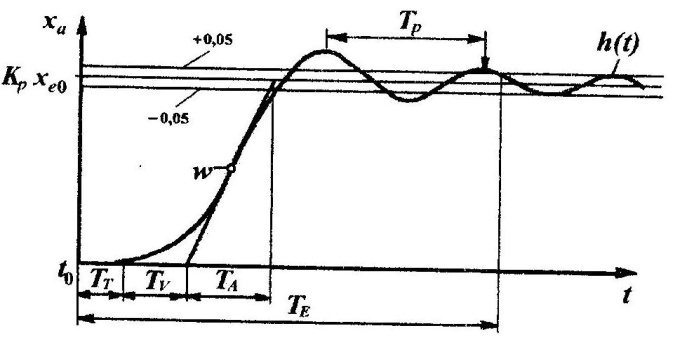 ремя задержки колебаний Т_v определяется по точке пересечения с осью абсцисс касательной в точке w перегиба графика. Время установления колебаний Т_А определяется моментом времени пересечения касательной в точке w с действительным значением х_a0 = KрXe₀. Период колебаний средства измерения равен Т_р. В качестве времени установления средства измерения Т_Е принимается интервал времени, по истечении которо­го выходная величина в затухающем колебательном переходном про­цессе перестает выходить за границы, превышающие ±0,05 (±5%) действительного значения x_a0 = КрХ_е0.

10. С использованием первой из формул Эйлера

cos α + i sin α) = exp(i α); cos α - i sin α = ехр(-iα)

где i= - мнимая единица (г = -1), входной и выходной перио­дические синусоидальные сигналы можно представить в экспоненци­альной форме в виде комплексной величины:

х_е = x_eQ[cosωt + isin(ωt)] = x_e0 exp(iωt),

х_а = x_o0[cos(ωt + δφ) + isin(ωt + δφ)] = х_а0 exp[i(ωt + δφ)] = х_а0 ехр(i ωt) ехр(δφ). (1.38)

Частотные характеристики - амплитудно-частотная и фазово-частотная - в совокупности образуют комплексный коэффици­ент передачи G(i ), равный отношению комплексных выходной и входной величин:

Комплексный коэффициент передачи G( ) можно представить как в тригоно­метрической, так и в обычной форме:G( ) = ReG + i*ImG, и изобразить графически на комплексной плоскости

С использованием производной в операторной форме (или комплексной частоты р = ), получаем передаточную функцию измерительного преобразователя с за­держкой второго порядка

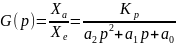,описывающую его динамические свойства.

Передаточная ф-ция G(p) СИ, характеризуемого временной задержкой, является величиной, аналогичной передаточ­ному коэффициенту К_р при статических измерениях.

Передаточную функцию для измерительного преобразователя с задержкой второго порядка можно представить в виде

При р = 0, что соответствует статическим измерениям, передаточ­ная функция будет равна для линейного преобразователя его переда­точному коэффициенту К_р.

Аналогично для измерительного преобразователя с задержкой первого порядка, переходный процесс которого описывается диффе­ренциальным уравнением (1.38), получим выражения для комплекс­ного коэффициента передачи и передаточной функции соответственно:

К динамич хар-кам СИ относятся также интервал рабочих частот, собственная (резонансная) частота колебаний самой системы при ее возбуждении в отсутствие внеш воздействий и добротность. Интервал рабочих частот - диапазон частот входного сигнала, в пределах кот. погрешность измерений не превышает допускаемого предела. При частоте входного сигнала, близкой к собственной частоте СИ (при ω ≈ω₀), имеет место явление резонанса, при кот. возрастает амплитуда выходного сигнала. Добротность Q СИ показывает, во сколько раз амплитуда выходного сигна­ла при резонансе превышает амплитуду входного сигнала. Доброт­ность системы есть умноженное на π число полных колебаний, по истечении которых амплитуда уменьшается в е раз; след-но, Q тем выше, чем меньше затухание колебаний в системе. Чем выше значение добротности, тем более четко проявляется резо­нанс, более узким является максимум амплитудно-частотной характе­ристики вблизи собственной частоты со₀. Значение добротности зави­сит от параметров средства измерения.

27. СВЧ электрическое поле с напряженностью Е возникает за счет возбуждения электромагнитных колебаний в объемных резонаторах генератора. Объемный резонатор обеспечивает необходимую для генерирования излучения положительную обратную связь и представляет собой замкнутую, например цилиндрическую с торце­выми стенками, полость с хорошо проводящими стенками, внутри которой могут осуществляться свободные электромагнитные колеба­ния. Торцевые электроды расположе­ны по обе стороны анодного блока перпендикулярно его оси. Принцип действия объем­ного резонатора.

Пусть имеем плоский конденсатор, обклад­ки которого выполнены в виде дисков.Между дисковыми обкладками кон­денсатора, включенного в цепь переменного тока, создается однородное по сечению пере­менное электрическое поле (ток смещения), которое порождает перемен­ное магнитное поле. Связь между электриче­ским и магнитным полями определяется урав­нением Максвелла

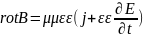которое в отсутствии токов проводимости(j=0) имеет вид Из уравнения следует, что изменяющееся во времени электрическое поле порождает вихревое магнитное поле. Силовые линии магнитного поля представляют собой окружности, центры которых расположены на оси конденсатора. С увеличением частоты изменения напряженности Е электрического поля увеличивается индукция В возбуждаемого переменного магнитного поля. Магнитное поле вызывает появление дополнительного электрического поля в соответствии с другим из уравнений Максвелла:

Возбужденное электрическое поле стре­мится уменьшить первоначальное электрическое поле, а также возбу­ждает дополнительное магнитное поле.Т.о. при высоких частотах плоский конденсатор объединяет в себе два элемента - ем­кость и индуктивность. При достаточно высокой частоте поочередное возбуждение магнитным полем электрического и электрическим -магнитного может проходить неоднократно. В результате нарушается однородность электрического поля между обкладками плоского кон­денсатора. Направление напряженности электрического поля может несколько раз изменяться при переходе от оси конденсатора к его краю. При этом на определенных расстояниях от оси, соответствую­щих точкам изменения направления вектора E, напряженность поля равна нулю. Если между обкладками плоского конденсатора поместить прово­дящий полый цилиндр, внутренний радиус которого r₀ соответствует нулю напряженности Е, то сила тока по стенкам такого цилиндра будет близкой к нулю. Внутри цилиндра могут существовать взаимо­связанные переменные электрическое и магнитное поля. Такой ци­линдр настроен на определенную резонансную частоту, зависящую от размеров цилиндра, и является объемным резонатором. В идеальном резонаторе сами по себе поля существовали бы бесконечно долго. Чтобы в реальном резонаторе поля не затухали, в резонатор вводят через боковое отверстие резонансной полости электромагнитную энергию резонансной частоты. В результате формируются электро­магнитные колебания с очень узкой полосой пропускания и высокой добротностью, достигающей ~10⁵ и выше.За счет электромагнитных колебаний, возбуждаемых в резонато­рах магнетронного генератора, вблизи щелей анода возникает сверх­высокочастотное электрическое поле. На электро­ны, испускаемые катодом и движущиеся от катода к аноду, действуют три поля: постоянное электрическое поле, постоянное магнитное поле и электрическое СВЧ поле резонаторной системы. Под действием по­стоянного электрического поля электроны приобретают радиальную скорость, при этом энергия источника анодного напряжения преобра­зуется в кинетическую энергию электронов. Под действием магнитно­го поля электроны приобретают тангенциальную составляющую ско­р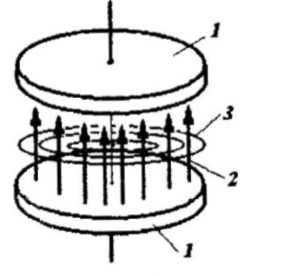 ости. СВЧ поле, проникающее через щели резонаторов в промежуток между катодом и анодом, либо тормозит электроны (если тангенци­альные составляющие скорости электронов и напряженности СВЧ поля совпадают по направлению), либо дополнительно ускоряет их (в противоположном случае).Под действием СВЧ поля и взаимно перпендикулярных (скрещен­ных) статических электрического и магнитного полей электроны ска­пливаются вблизи щелей и образуют сгустки (спицы). При взаимо­действии с СВЧ полем электроны в сгустках отдают полю кинетиче­скую энергию и под действием постоянного электрического поля приближаются к аноду. Они достигают анода, отдав электромагнит­ному полю почти всю энергию, что обусловливает высокий (до 90%) КПД Этим процессом обеспечивается возможность приборов магне­тронного типа усиливать и генерировать СВЧ колебания.

Пояснения к рисунку(Схема принципа действия объемного резонатора):1-торцевые электроды обкладки конденсатора;2-силовые линии электрического поля;3-силовые линии магнитного поля;

28. Работа прибора основана на длительном взаимодействии электромагнитной волны и электронного потока, направленных противоположно друг другу. При увеличении напряжения, ускоряющего электроны, возрастают ско­рость электронов и частота переменного электрического поля, при которой происходит взаимодействие. Это дает возможность элек­тронной перестройки частоты генерируемого излучения.

П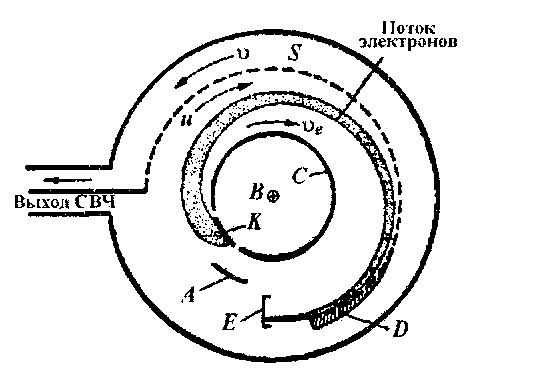 ринцип действия. Элек­троны эмиттируют из нагреваемого катода К и под действием уско­ряющего напряжения, приложенного между катодом К и анодом А, приобретают начальную скорость. Постоянное магнитное поле, ин­дукция которого В направлена вдоль оси лампы, искривляет траекто­рию электронов. Для фор­мирования электронного пучка используется допол­нительный электрод С. По­ток электронов, движущий­ся во взаимно перпендику­лярных электрическом и магнитном полях, проходит вблизи замедляющей сис­темы S, которая применяет­ся для уменьшения фазовой скорости электромагнитной волны. Эффективное взаи­модействие электромагнит­ной волны и электронного потока происходит при условии, что средняя скорость электронов близка к фазовой скорости волны (условие синхронизма элек­тронов и волн). Электроны под действием электрического и маг­нитного полей двигаются по сложным криволинейным траекториям. При выполнении условия синхронизма воздействие поля волны на электроны приводит к образованию сгустков электронов, которые на участке движения в направлении силовых линий затормаживаются полем и отдают ему при этом часть своей энергии. После взаимодей­ствия электроны попадают на коллектор Е, а генерируемое электро­магнитное излучение направляется на выход из прибора. Вблизи кол­лектора электронов расположен слой D поглотителя электромагнит­ного излучения, отраженного от выхода. Фазовая и и групповая и ско­рости электромагнитной волны в лампе обратной волны направлены в противоположные стороны (отрицательная дисперсия), и энергия электромагнитной волны распространяется на­встречу электронному потоку. Разнонаправленность скоростей элек­тронов и групповой скорости волны создает положительную обрат­ную связь, что и позволяет генерировать энергию электромагнитного излучения.

Основным условием, при котором электрическое СВЧ поле груп­пирует электроны в сгустки пространственного заряда и тормозит большую часть электронов, отбирая у них энергию, полученную от постоянного электрического поля, является условие синхронизма электронов и волн. Условие синхронизма:состав­ляющая средней скорости, характеризующая переносное движение электронов, должна быть равна фазовой скорости СВЧ волны.

Для достижения условия синхронизма электронов и волн осущест­вляют замедление электромагнитных волн с помощью замедляющих систем. Замедляющая система - устройство, позволяющее уменьшить фазовую скорость электромагнитной волны. По конструкции раз­личают спиральные, резонансные и штыревые замедляющие системы.

Замедляющая система характеризуется коэф­фициентом замедле­ния n, равным отноше­нию скорости распро­странения с электромаг­нитной ВОЛНЫ в свободном пространстве к ско­рости ее распространения в среде, волноводе или замедляющей сис­теме. Для электромагнитной волны в средах коэффициент замедления п называют показателем преломления. Различают коэффициент замедления фазовой скорости n=c/v и коэффициент за­медления групповой скорости n_g=c/u.Величины nи n_gсвя­заны между собой формулой Рэлея

n_g=n-λ(dn/dλ)

что следует из соотношения между фазовой v и групповой и скоро­стями

u = v-λ(dv/dλ)

где dv/dλ -дисперсия электромагнитной волны; dn/dλ -дисперсия среды, в которой распространяется волна.

Условие синхронизма электронов и волн требует выполнения со­отношения

,где

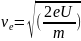
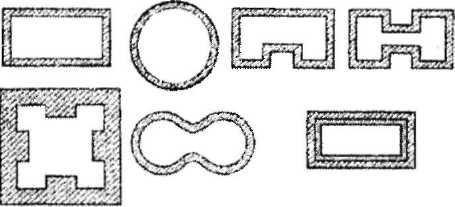29. Передача СВЧ излучения в определенном направлении с возмож­ностью изменения направления передачи осуществляется с помощью волноводов. Волноводы для электромагнитных волн обычно пред­ставляют собой полые или частично заполненные диэлектриком ме­таллические трубы либо стержни из диэлектрика.Преиму­щественное распространение получили волноводы прямоугольного сечения. Полые волноводы используются в диапазоне длин волн 0,2-30 см; металлические волноводы, частично заполненные диэлектриком (преимущественно прямоугольного и кругового сечений), применяются в диапазоне миллиметровых волн в основном для пере­дачи сигналов повышенной мощности.

Механизм распростра­нения электромагнитной волны в волноводе обу­словлен ее многократным отражением от стенок вол­новода. При наклонном па­дении электромагнитной волны на плоскую отра­жающую поверхность за счет наложения падающей и отраженной волн образуют­ся: бегущая волна в направлении, параллельном отражающей поверх­ности, и стоячая волна, расположенная вдоль направления, перпенди­кулярного к этой поверхности. В узлы стоячей волны можно помес­тить идеально проводящую тонкую металлическую пластину без ис­кажения поля. Такая пластина будет расположена параллельно отра­жающей поверхности на расстоянии от нее, равном длине стоячей волны. Образующаяся при отражении от обеих поверхностей бегущая волна будет переносить электромагнитную энергию.

Волноводы и резонаторы характеризуются волновым сопро­тивлением. Для полых волноводов различают волновое сопротивле­ние двух типов. Волновое сопротивление первого типа назы­вается характеристическим сопротивлением и определяется отношением поперечных к оси волновода компонентов напряженностей электрического и магнитного полей. Оно не зависит от размера волновода и характеризует лишь тип волны в нем; для волн, исполь­зуемых для передачи сигналов,

где ε и µ - диэлектрическая и магнитная проницаемости среды в вол­новоде; λ₀ и λ_в - длины волн соответственно в свободном пространст­ве и в волноводе. Волновое сопротивление второго типа вы­ражается как отношение амплитудных значений напряжения и тока в любом сечении волновода:

Волновое сопротивление резонатора - величина, равная реактив­ной части полного сопротивления одной из ветвей (индуктивной или емкостной) параллельного колебательного контура, эквивалентного данному резонатору, при резонансной частоте ωo :

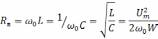
где U_m- амплитуда напряжения между точками резонатора, по отно­шению к которым определяется волновое сопротивление; L и С - ин­дуктивность и емкость параллельного контура; W - энергия, запасен­ная в резонаторе.

Рис.( Прим.поперечных сечений полых волноводов в виде метал. Труб)

24. Электромагнитное излучение - распространяющиеся в пространстве электромагнитные колебания (взаимосвязанные переменные электрическое и магнитное поля (электромагнитная волна)), или поток квантов электромагнитной энергии –фотонов.

Электромагнитная волна является поперечной волной, в которой векторы напряженности электрич-го Е и магнитного H полей колеблются (периодически изменяются) во взаимно перпендикулярных плоскостях. Эти векторы составляют с вектором Пойтинга S=[E х H], определяющим направление распространения энергии монохроматической электомагнитной волны, правую тройку.

Ур-ие плоской электромагнитной волны, записанное для модуля вектора напряженности электрического поля Е (в оптике- светового вектора), имеет вид Е = )

Где - амплитудное значение; х - координата вдоль направления распространения волны; t – время; - частота распростр-ся электромагнитных колебаний; L- длина волны.

Основными харак­теристиками электро­магнитной волны яв­ляются: частота v и длина волны L = /ν, где - фазовая ско­рость распространения волны. Используются также циклическая частота = 2nv и волновое число к= 2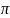 /L = / . Волна, в которой распростр-иеся коле­бания имеют определенную строго заданную частоту и неизменную амплитуду, является монохроматич. Энергия монохромати­ч волны переносится в пространстве со скоростью, равной фазо­вой скорости (завис от среды распространения).

Скорость света в среде зависит от показателя преломления среды п, различного для различных частот электромагнитного излучения. Зависимость показателя преломления среды от частоты называют дисперсией среды, а фазовой скорости от частоты - дисперсией света. Если электромагнитная волна не является монохроматической, то энергия волны переносится со скоростью, отличной от фазовой. Такая скорость называется групповой. В вакууме фазовая и групповая скорости равны.

Во многих процессах электромагнитное излучение проявляет кор­пускулярные свойства. При учете корпускулярной природы электро­магнитное излучение рассматривается как поток квантов электромаг­нитной энергии = hv, где h = 6,626*10-³⁴ Дж*с- постоянная Планка (квант действия). Квант электромагнитного излучения рас­сматривается как элементарная частица - фотон, - обладающая энер­гией = hv,импульсом р=h и рядом других квантовых хар-к. Скорость света в вакууме с и постоянная Планка h являются фундаментальными физическими константами.

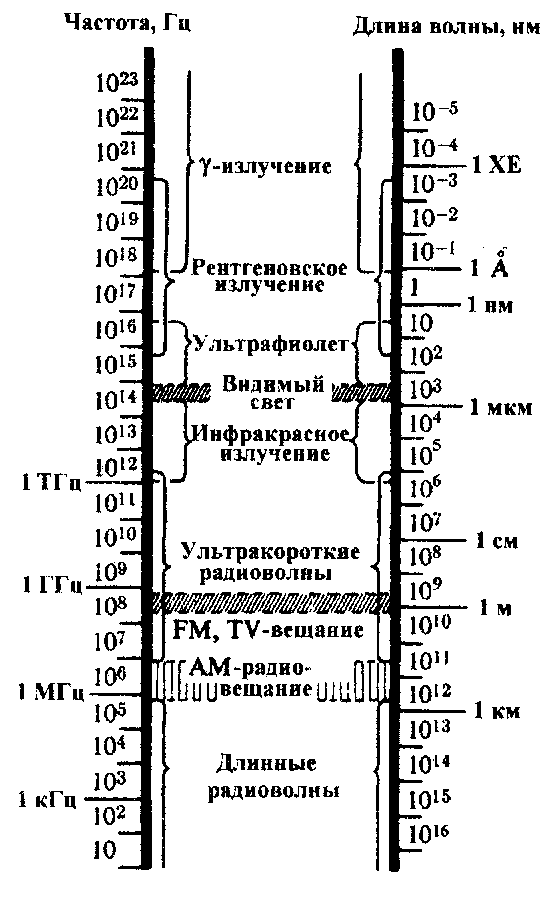
Шкала электромагнитных волн представленна в порядке изменения длины волны L и частоты v излучения (v = с/L.) на рис.1.

Электромагнитные волны с частотами v = 3*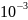 -3*10⁴ Гц и длина­ми L=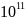 -10⁴ м, возбуждаемые переменными электрическими токами в различных устройствах, относящиеся к низкочастотным (сверх­длинным), на рисунке не отображены.

Затем в порядке возрастания частоты следует диапазон радиоволн с широким интервалом частот: v = 3*10⁴-3*10¹² Гц и длин волн: L = - м. Радиоволны возбуждаются за счет электромагнитных колебаний в вибраторах (электрических колебательных контурах) специальных радиопередающих устройств. Они могут генерировать­ся, излучаться и приниматься радиоаппаратурой. Радиоволны, в свою очередь, подразделяют на длинные (v = 3-10⁴—3-10⁵ Гц), средние (у = 3-10⁵-3-10⁶Гц), короткие (v = 3-10⁶-3-10⁷ Гц) (радиовещание амплитудно-модулированными (AM) сигналами), ультракороткие (v = 3-10⁷—3-10" Гц) и субмиллиметровые (v = 310"-3-10¹² Гц). Ульт­ракороткие радиоволны, в свою очередь, подразделяют на метровые (L = 10—1 м) и дециметровые (L = 10-1 дм) (радиовещание передачей частотно-модулированных (FM)

сигналов и телевизионное вещание), сантиметровые (L = 10-1 см) (радиолокация) и миллиметровые (L = 10-1 мм).

В измерительной технике при реализации ряда аналитических ме­тодов, а также в технологических процессах достаточно широко ис­пользуется электромагнитное сверхвысокочастотное (СВЧ) из­лучение, интервал частот которого v = 300 МГц - 300 ГГц. Это из­лучение охватывает дециметровые, сантиметровые и миллиметровые волны. В соответствующий этому излучению диапазон частот входят частоты колебаний молекул веществ, а также частоты переходов элек­тронов в атомах между энергетическими подуровнями. СВЧ излуче­ние используется в качестве анализирующего в аналитических мето­дах, объединенных названием микроволновая спектроскопия, или радиоспектроскопия.

Далее следует оптический диапазон электромагнитного излучения. К оптическому диапазону обычно относят инфракрас­ное, видимое и ультрафиолетовое излучения, испускание которых обусловлено переходами оптических электронов атомов, расположен­ных на внешних электронных оболочках. Природа электромагнитного излучения в видимой области спектра, а также ультрафиолетового и рентгеновского излучений - электронные переходы в атомах. Харак­теристическое рентгеновское излучение испускается при переходе электронов из более возбужденных состояний на внутренние элек­тронные оболочки атомов.

Инфракрасное (ИК) излучение характеризуется частотами у = 310¹²-3,95-10^,4Гц и длинами волн L = 10^_4-0,7410м. Оно ис­пускается веществом за счет колебательного движения молекул и электронных переходов в атомах. ИК излучение подразделяется на следующие диапазоны: далекое (X = 50-2000 мкм), среднее (L = 2,5-50 мкм) и ближнее (L - 0,74-2,5 мкм).

Более высоким частотам соответствует очень узкий и очень важный диапазон оптического излучения - видимый свет. Электромагнитные волны, соответствующие видимому свету, имеют длины L = 380-740 нм.

Ультрафиолетовое (УФ) электромагнитное излучение имеет длины волн L = 380-10 нм и подразделяется на ближнее (L = 380-200 нм) и крайнее (вакуумный ультрафиолет) (L = 200-10 нм).

Рентгеновское излучение характеризуется длинами волн L = 10²-10^-5 нм и энергиями фотонов = hv = 100 эВ - 1 МэВ. Его подразделяют на мягкое (L > 0,2 нм) и жесткое (L < 0,2 нм).

Радиоактивное -изл учение может сопровождать процессы 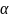- и ( -распада атомных ядер, а также испускаться при ядерных реакциях. Ему соответствуют следующие значения частот: v > 3-Ю¹⁸ Гц и длин волн: L.<0,1 нм. у-излучение испускается при переходах ядер атомов из более возбужденных состояний в менее возбужденные.

25.Генераторные лампы - электровакуумные электронные при­боры, предназначенные для преобразования энергии источника посто­янного или переменного тока в энергию высокочастотных электро­магнитных колебаний.

Рассмотрим принцип действия простейшего лампового генератора, состоящего из вакуумного триода и колебательного контура.

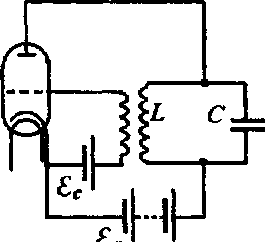В контуре под влиянием случайных электрических колебаний возникают собственные колебания тока и напря­жения. Чтобы колебания в контуре не затухали из-за потерь энергии, ее не­обходимо пополнять. Это осуществля­ется с помощью триода: переменное напряжение, поступающее от контура к сетке триода через трансформатор­ную связь, вызывает изменение анод­ного тока; в результате в цепи анода появляются пульсации тока, которые электромагнитных колебаний при правильном подборе фазы напря­жения, подаваемого на сетку лампы (цепь обратной связи), будут по­полнять энергию колебательного контура (положительная обратная связь).

Если пополнение энергии в колебательном контуре превосхо­дит потери ее за то же время, то амплитуда начальных колебаний, возникших в контуре, будет расти. Однако по мере нарастания ампли­туды колебаний коэффициент усиления уменьшается за счет нелиней­ности вольтамперной характеристики триода. В результате устанав­ливается стационарная амплитуда генерируемых колебаний. Частота v электромагнитных колебаний определяется при этом параметрами колебательного контура - электроемкостью С и индуктивностью L. Так, частота генерируемых колебаний будет равна резонансной часто­те колебательного контура:

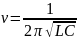
В области частот, соответствующих СВЧ излучению, существен­ными становятся емкости и индуктивности деталей не только элек­тронной схемы генератора, но и самого вакуумного триода. Поэтому в генераторных лампах СВЧ диапазона внешний колебательный контур отсутствует, а роль элементов колебательного контура выполняют межэлектродные емкости и индуктивности самих электродов вакуум­ного триода. Наиболее распространенными генераторными лампами являются металлокерамические триоды.

На рис. представлена конструкция металлокерамического генераторного триода средней мощности. Основными рабо­чими элементами триода являются нагреваемый катод 7, эмиттирующий электроны, анод 5 и сетка 6. Эти электроды расположены на оп­ределенных достаточно близких расстояниях друг от друга; их по­верхности параллельны. Межэлектродные емкости и индуктивности электродов (совместно с их цилиндрическими вывода­ми) играют роль элементов колебательного контура, в котором возбуждаются электромагнитные колеба­ния соответствующей час­тоты. Электроды разделены керамическими изолятора­ми /, которые плотно со­единены с металлическими электродами. При изготов­лении триода осуществля­ется высоковакуумная от­качка его рабочего объема через штенгель 2, верхний конец которого после отсо­единения от откачивающей вакуумной системы герме­тизируется. Для воздушного охлаждения работающего триода применяется метал­лический радиатор 3. Ци­линдрические выводы 4 и 9 электродов метал­лический радиатор 3. Ци­линдрические выводы 4 и 9 электродов предназначены для подачи на электроды соответствующих напряже­ний и приспособлены к не­посредственному подклю­чению генератора к резонаторной колебательной системе, например к объемному резонатору.

В общем случае генераторные лампы различают по числу электро­дов (триоды, тетроды, пентоды), роду работы (непрерывного действия и импульсные), уровню мощности (малой мощности - до 25 Вт, сред­ней мощности - до 1 кВт, мощные - до 200 кВт, сверхмощные - свы­ше 200 кВт), диапазону рабочих частот (коротковолновые (KB) - до 30 МГц, ультракоротковолновые (УКВ) - до 300 МГц, сверхвысоко­частотные (СВЧ) - свыше 300 МГц). С целью увеличения мощности генерируемых электромагнитных колебаний используются нагревае­мые катоды с большой - в десятки квадратных сантиметров - эмиттируюшей поверхностью.

26.Для генерирования электромагнитных колебаний более высоких частот СВЧ диапазона используются магнетронные генераторы. Магнетрон, в общем случае, прибор, принцип действия которого основан на движении заряженных частиц, в частности электронов, во взаимно перпендикулярных электрическом и магнитном полях.

Принцип действия магнетронных генераторов СВЧ излучения ос­нован на взаимодействии электронов, движущихся в электрическом и магнитном полях по криволинейным траекториям, с возбуждаемым электромагнитным полем. В магнетронном генераторе энергия посту­пает от источника анодного напряжения, колебательной системой яв­ляются объемные резонаторы, а функции активного элемента выпол­няет поток электронов.

Анод 1магнетронного генератора представляет собой массивный полый цилиндр, изготовленный чаще всего из меди, во внутренней части которого вырезаны объемные резонаторы 2 со ще­лями, выходящими на внутреннюю поверхность цилиндра. Вдоль оси цилиндра расположен также цилиндрический накаляемый катод 4. Электроны эмиттируют из нагреваемого катода. Под действием маг­нитного поля, индукция которого направлена также параллельно оси цилиндра, траектория электронов искривляется (рис. 2.7). Постоянные электрическое и магнитное поля создаются в пространстве взаимодействия внешними источниками: электрическое с напряженностью Е - напряжением между катодом и анодом (анодным напряжением); магнитное с индукцией В - током, пропускаемым по обмотке внеш­ней катушки. Под действием сил со стороны электрического (F_e = еЕ) и магнитного (F_m =е х В) полей электроны движутся по сложным траекториям, но с определенной средней скоростью.

Рис.2.6. Схема многорезонаторного магнетронного генератора СВЧ излучения: / - анод; 2 - резонатор; 3 - выводы нагревателя катода; 4 - катод; 5 - петля связи для вывода СВЧ энергии; 6 - устройство вывода СВЧ энергии.

5. Измерение, состоящее в сравнении измеряемой величины с величиной меры, есть процесс преобразования, в результате которого измеряемая величина не отображается другой величиной Xа. Это преобразование реализуется функциональным элементом измерительного прибора, который называется измерительным преобразователем.

Измерительный преобразователь - это техническое устройство, созданное на определенном физическом принципе действия, выполняющее одно частное измерительное преобразование, т.е. преобразующее входную физическую величину в другую физическую величину или в соответствующий сигнал отображения, удобный для последующих преобразований, обработки и хранения, и имеющее нормированные метрологические характеристики.

Физическая величина Xе подаваемая на вход преобразователя, называется входной; величина Xа, отображающая входную величину, называется выходной.

В общем случае алгоритм преобразования можно представить в виде Xа=f(Xе), где f - функция преобразования.

Схематич процесс измерения можно представить следующим обобщенным образом: