27 . Основная теорема зацепления (теорема Виллиса)
Для постоянства передаточного отношения при зацеплении двух профилей зубьев необходимо, чтобы радиусы начальных окружностей зубчатых колёс, перекатывающихся друг по другу без скольжения, оставались неизменными. Если рассмотреть обращённое движение начальных окружностей, когда всей системе задана угловая скорость (), то второе колесо будет условно неподвижным и точка Р является мгновенным центром относительного вращения колёс (рис. 70,а). Эта точка, называемая полюсом зацепления, где контактируют начальные окружности, делит межцентровое расстояние на отрезки, обратно пропорциональные угловым скоростям, т. к.
.
i12=w1/w2=rw2/rw1=const rw=const
Рассмотрим обращённое движение профилей зубьев зубчатых колёс
рис. 70
Точка контакта зубьев (точка к), принадлежащая первому колесу, вращается вокруг точки Р, которая будет мгновенным центром скоростей. Скорость и совпадает с общей касательной к профилям в точке к при условии постоянства этого контакта.
В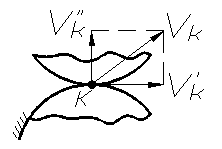
противном случае постоянного контакта
не будет, так как появится составляющая
и профили разомкнутся (рис. 71). Так как
рассматривается произвольное положение
зубьев, то можно сформулировать теорему.
Нормаль NN к касающимся профилям
зубьев, проведённая через точку их
касания, делит межцентровое расстояние
на части, обратно пропорциональные
угловым скоростям. Эта теорема,
сформулированная Виллисом в 1841 г.,
определяет основной закон зацепления
профилей, которые не могут быть
произвольными, а должны быть специально
подобраны.
28. Основные элементы эвольвентного зацепления. Анализ эвольвентного зацепления.Эвольвентное зацеплениеПодавляющее большинство зубчатых передач, применяемых в технике, имеет зубчатые колеса с эвольвентным профилем. Эвольвента как кривая для формирования профиля зуба была предложена Л. Эйлером. Она обладает значительными преимуществами перед другими кривыми, применяемыми для этой цели, – удовлетворяет основному закону зацепления, обеспечивает постоянство передаточного отношения, нечувствительна к неточностям межосевого расстояния (что облегчает сборку), наиболее проста и технологична в изготовлении, легко стандартизируется (что особенно важно для такого распространенного вида механизмов как зубчатые передачи).Эвольвента – это траектория движения точки, принадлежащей прямой, перекатывающейся без скольжения по окружности. Данная прямая называется производящей прямой, а окружность, по которой она перекатывается – основной окружностью (рисунок 38 а).
Эвольвента обладает следующими свойствами, которые используются в теории зацепления:
1) форма эвольвенты определяется радиусом основной окружности;
2) нормаль к эвольвенте в любой ее точке является касательной к основной окружности. Точка касания нормали с основной окружностью является центром кривизны эвольвенты в рассматриваемой точке;
3) эвольвенты одной и той же основной окружности являются эквидистантными (равноотстоящими друг от друга) кривыми.
Положение любой точки на эвольвенте может быть однозначно охарактеризовано диаметром окружности, на которой она расположена, а также характерными для эвольвенты углами: углом развернутости (обозначается ν), углом профиля (α), эвольвентным углом – invα (рисунок 38 б). На рисунке 38 б показаны эти углы для произвольно выбранной на эвольвенте точки Y, поэтому они имеют соответствующий индекс:
- νY – угол развернутости эвольвенты до точки у;
- αY – угол профиля в точке Y;
- invαY – эвольвентный угол в точке Y (на окружности диаметра dY ).
29Основные геометрические элементы зубчатого колеса
Зубчатое звено (колесо, рейка или сектор) состоит из тела звена и зубчатого венца. В дальнейшем будем рассматривать зубчатые колеса, распространяя присущие им свойства на остальные звенья ввиду общности строения их венцов. Форма колеса зависит от взаимного расположения осей вращения зубча тых колес в передаче: цилиндрическая – при параллельных осях, коническая – при пересекающихся осях и гиперболоидная– при перекрещивающихся осях. Колесо – пространственное тело, но для изучения большинства его геометрических элементов и свойств достаточно рассмотреть любое торцовое сечение колеса (сечение плоскостью перпендикулярной его оси), т. к. в остальных торцовых сечениях сохраняется та же геометрия, которая наблюдается в выбранном торцовом сечении. Венец цилиндрического зубчатого колеса в торцовом сечении (рис. 1) представлен контуром, очерченным отрезками кривых линий. Венец заключен между двумя соосными окружностями: между окружностью вершин зубьев диаметра da и окружностью впадин диаметра d f .Положение венца относительно оси колеса зависит от числа зубьев и задается делительной окружностью диаметра d , которая расположена между ок-ружностью вершин и окружностью впадин, ближе к окружности вершин. Этоглавная геометрическая окружность колеса. С ее помощью определяют радиальные размеры колеса. Она делит зубья по высоте на две неравные части: делительную головку высотой ha и делительную ножку высотой hf . Делительная головка короче делительной ножки на величину радиального зазора с . О радиальном зазоре см. 1.2.
30.
Модулем зацепления называется линейная
величина в p раз
меньшая окружного шага или отношение
шага по любой концентрической окружности
зубчатого колеса к p .
В зависимости от окружности по которой
определен модуль различают делительный,
основной, начальный. Для косозубых колес
еще и нормальный, торцевой и осевой
модули
-
диаметр окружности произвольного
радиуса,
-
диаметр делительной окружности,
-
шаг по окружности произвольного
радиуса,
-
шаг по делительной окружности,
Радиус
окружности вершин
Высота
зуба
Р
адиус
окружности впадин
Толщина
зуба по делительной окружности. Так как
стночно-начальная прямая перекатывается
в процессе огибания по делительной
окружности без скольжения, то дуга s-s по
делительной окружности колеса равна
ширине впадины e-e по
станочно-начальной прямой инструмента.
Тогда, c учетом схемы на рис. 12.5, можно
записать
3
1.
Cуществует
два принципиально различных метода
нарезания: 1) метод копирования; 2)
метод обкатки. В первом случае впадина
зубчатого колеса фрезеруется на
универсальном фрезерном станке фасонными
дисковыми или пальцевыми фрезами,
профиль которых соответствует профилю
впадины (рис. 76). Затем заготовку
поворачиваютна угол 360º/Z и
нарезают следующую впадину. При этом
используется делительная головка, а
также имеются наборы фрез для нарезания
колёс с различным модулем и различным
числом зубьев. Метод непроизводителен
и применяется в мелкосерийном и единичном
производстве. Второй метод обката или
огибания может производиться с помощью
инструментальной рейки (гребёнки) на
зубострогальном станке; долбяком на
зубодолбёжном станке или червячной
фрезой на зубофрезерном станке. Этот
метод высокопроизводителен и применяется
в массовом и крупносерийном производстве.
Одним и тем же инструментом можно
нарезать колёса с различным числом
зубьев. Нарезание с помощью инструментальной
рейки имитирует реечное зацепление
(рис. 77, а), где профиль зуба образуется
как огибающая последовательных положений
профиля инструмента, угол исходного
контура которого α=20º (рис. 77, б). Зацепление
между режущим инструментом и нарезаемым
колесом называется станочным.
В станочном зацеплении начальная
окружность всегда совпадает с делительной.
Самым производительным из рассмотренных
методов является зубофрезерование с
помощью червячных фрез, которые находятся
в зацеплении с заготовкой по аналогии
с червячной передачей (рис. 77, в). При
нарезании долбяком осуществляется его
возвратно поступательное движение при
одновременном вращении. Фактически при
этом осуществляется зацепление
заготовки с инструментальным
зубчатым колесом – долбяком (рис.
77, г). Этот метод чаще всего используется
при нарезании внутренних зубчатых
венцов.
34) Изобразим сопряжённые профили у полюса зацепления. Так как линия является общей касательной к основным окружностям, то, исходя из геометрии построения эвольвенты, профили зубьев всегда будут касаться только на этой линии. Линия всегда будет перпендикулярна к сопряжённым профилям. Поэтому линию принято называть линией зацепления.Линия зацепления — геометрическое место точек контакта двух сопряжено работающих профилей.На линии различают теоретический и рабочий участки линии зацепления.Теоретический участок — отрезок между основаниями перпендикуляров, опущенных на линию зацепления из центров.Практический или рабочий участок — участок линии зацепления, ограниченный внешними окружностями колёс.Если за пределами теоретического участка частично окажется рабочий участок, то нарушится постоянство передаточного соотношения. Чтобы передаточное отношение было постоянным необходимо, чтобы рабочий участок находился в пределах теоретического.Изобразим профили зубьев в момент встречи и расставания, и отметим на начальной окружности положение профилей при встрече и расставании. Дуга на начальной окружности есть путь в процессе контакта. Дуга - дуга зацепления на основной окружности.Коэффициент перекрытия - коэффициент, показывающий количество шагов, укладывающихся в дуге зацепления, . - угол зацепления. Угол зацепления гостирован, так как положение нормали определяет кривизну профиля.Коэффициент перекрытия оптимален, если он больше единицы. Чем больше коэффициент перекрытия , тем лучше работает передача, то есть улучшается плавность зацепления. Если коэффициент перекрытия меньше единицы, то встречи и расставания зубьев будут сопровождаться ударами.
35) Эвольвентное зацеплениеПодавляющее большинство зубчатых передач, применяемых в технике, имеет зубчатые колеса с эвольвентным профилем. Эвольвента как кривая для формирования профиля зуба была предложена Л. Эйлером. Она обладает значительными преимуществами перед другими кривыми, применяемыми для этой цели, – удовлетворяет основному закону зацепления, обеспечивает постоянство передаточного отношения, нечувствительна к неточностям межосевого расстояния (что облегчает сборку), наиболее проста и технологична в изготовлении, легко стандартизируется (что особенно важно для такого распространенного вида механизмов как зубчатые передачи).Эвольвента – это траектория движения точки, принадлежащей прямой, перекатывающейся без скольжения по окружности. Данная прямая называется производящей прямой, а окружность, по которой она перекатывается – основной окружностьюЭвольвента обладает следующими свойствами, которые используются в теории зацепления:1) форма эвольвенты определяется радиусом основной окружности;2) нормаль к эвольвенте в любой ее точке является касательной к основной окружности. Точка касания нормали с основной окружностью является центром кривизны эвольвенты в рассматриваемой точке;3) эвольвенты одной и той же основной окружности являются эквидистантными (равноотстоящими друг от друга) кривыми. Положение любой точки на эвольвенте может быть однозначно охарактеризовано диаметром окружности, на которой она расположена, а также характерными для эвольвенты углами: углом развернутости (обозначается ν), углом профиля (α), эвольвентным углом – invα (рисунок 38 б). На рисунке 38 б показаны эти углы для произвольно выбранной на эвольвенте точки Y, поэтому они имеют соответствующий индекс:- νY – угол развернутости эвольвенты до точки у;- αY – угол профиля в точке Y;- invαY – эвольвентный угол в точке Y (на окружности диаметра dY ).