15. Принцип неопределенности. Гейзенберг, Планк,Шредингер.

Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых , описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределенностей[* 1] задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Принцип неопределённости, открытый Вернером Гейзенбергом в 1927 г., является одним из краеугольных камней квантовой механики.

h-постоянна Планка 1,054*10 в -34 степени. коэффициента, связывающего угловую частоту ( — частота) фотона (или другого кванта) с его энергией

16. Опыт Резерфорда. Основные задачи и выводы.

Опыт Резерфорда (1906 г.) по рассеянию быстрых заряженных частиц при прохождении через тонкие слои вещества позволили исследовать внутреннюю структуру атомов. В этих опытах для зондирования атомов использовались – частицы – полностью ионизированные атомы гелия, – возникающие при радиоактивном распаде радия и некоторых других эле-ментов. Этими частицами Резерфорд бомбардировал атомы тяжелых металлов.

Резерфорду было известно, что атомы состоят из легких отрицательно заряженных частиц – электронов и тяжелой положительно заряженной частицы. Основная цель опытов – выяснить, как распределен положительный заряд внутри атома. Рассеяние – частиц (то есть изменение направления движения) может вызвать только положительно заряженная часть атома.

Опыты показали, что некоторая часть частиц рассеивается на большие углы, близкие к 180, то есть отбрасывается назад. Это возможно только в том случае, если положительный заряд атома сосредоточен в очень малой центральной части атома – атомном ядре. В ядре сосредоточена также почти вся масса атома.

Оказалось, что ядра различных атомов имеют диаметры порядка 10-14 – 10-15 см, в то время как размер самого атома 10-8 см, то есть в 104 – 105 раз превышает размер ядра.

Таким образом, атом оказался «пустым».

На основании опытов по рассеянию частиц на ядрах атомов Резерфорд пришел к плане-тарной модели атома. Согласно этой модели атом состоит из небольшого положительно заряженного ядра и обращающихся вокруг него электронов.

С точки зрения классической физики такой атом должен быть неустойчив, так как электроны, движущиеся по орбитам с ускорением, должны непрерывно излучать электромагнитную энергию.

17.Понятия колебаний механических систем. Малые колебания. Вынужденные колебания. Затухающие колебания. Примеры и основные

идеи и результаты.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие коле-

баний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение

тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестно-

сти положения равновесия. Положением равновесия называется такое состояние системы, в

котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение рав-

новесия — это положение маятника при отсутствии отклонения. В этом положении маятник,

если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз

проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл поло-

жение равновесия, достиг противоположного крайнего положения, на мгновение остановился в

нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад.

Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения рав-

новесия.

Период колебаний T — это время одного полного колебания. Можно сказать, что за период

тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: = 1=T. Частота измеряется в

герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

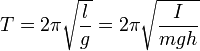
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида   в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний   или её квадрата.