18. Экстремум функции двух переменных

Определение 1.11. Пусть задана функция двух переменных z=z(x,y), (x,y) D. ТочкаM₀(x₀;y₀) - внутренняя точка области D.

Если в D присутствует такая окрестность UM₀ точки M₀, что для всех точек

то точка M₀ называется точкой локального максимума. А само значение z(M₀) - локальным максимумом.

А если же для всех точек

то точка M₀ называется точкой локального минимума функции z(x,y). А само значение z(M₀) - локальным минимумом.

Локальный максимум и локальный минимум называются локальными экстремумами функции z(x,y). На рис. 1.4 поясняется геометрический смысл локального максимума: M₀ - точка максимума, так как на поверхности z =z (x,y) соответствующая ей точка C₀ находится выше любой соседней точки C (в этом локальность максимума).

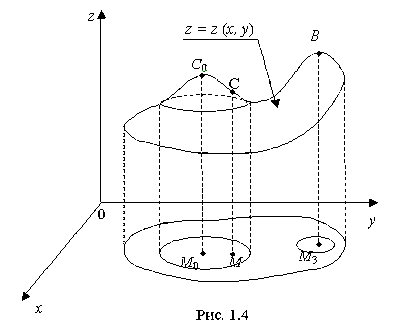
Заметим, что на поверхности в целом есть точки (например, В), которые находятся выше C₀, но эти точки (например, В) не являются "соседними" с точкой C₀.

В частности, точке. В соответствует понятие глобального максимума:

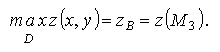
Аналогично определяется и глобальный минимум:

Нахождение глобальных максимумов и минимумов будет рассмотрено в п.1.10.

Теорема 1.3 (необходимые условия экстремума).

Пусть задана функция z =z (x,y), (x,y) D. Точка M₀(x₀;y₀ D - точка локального экстремума.

Если в этой точке существуют z'_x и z'_y, то

Геометрическое доказательство "очевидно". Если в точке C₀ на (рис.1.4) провести касательную плоскость, то она "естественно" пройдет горизонтально, т. е. под углом 0° к оси Ох и к оси Оу.

Тогда в соответствии с геометрическим смыслом частных производных (рис.1.3):

что и требовалось доказать.

Определение 1.12.

Если в точке M₀ выполняются условия (1.41), то она называется стационарной точкой функции z (x,y).

Теорема 1.4 (достаточные условия экстремума).

Пусть задана z =z (x,y), (x,y) D, которая имеет частные производные второго порядка в некоторой окрестности точки M₀(x₀,y₀) D. Причем M₀ - стационарная точка (т. е. необходимые условия (1.41) выполнены). Вычислим:

Если:

Доказательство теоремы использует темы (формула Тейлора функции нескольких переменных и теория квадратичных форм), которые в этом пособии не рассматриваются.

1. Определенный интеграл

Пусть функция y=f(x) определена на отрезке [a,b], а<в. Разобьем этот отрезок на n произвольных частей точками: а=х₀<х₁<х₂<…<х_i-1<х_i<х_n=b.

Обозначим это разбиение через τ, a точки x₀, x₁,…,x_n будем называть точками разбиения. В каждом из полученных частичных отрезков [x_i-1,x_i] выберем произвольную точку ξ_i(x_i-1 ξ_i x_i). Через Δx_iобозначим разность x_i-x_i-1, которую условимся называть длиной частичного отрезка [x_i-1, x_i].

Образуем сумму:

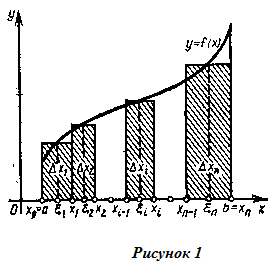
которую назовем интегральной суммой для функции f(x) на [a,b], соответствующее данному разбиению [a,b] на частичные отрезки и данному выбору промежуточных точек ξ_i. Геометрический смысл суммы σ очевиден: это сумма площадей прямоугольников с основаниями Δx₁, Δx₂, … , Δx_n и высотами f(ξ_i), f(ξ₂), … , f(ξ_n) (рис 1) (если f(x) 0).

Обозначим через λ длину наибольшего частичного отрезка разбиения τ: 

ОПРЕДЕЛЕНИЕ. Если существует конечный предел I интегральной суммы (1) при λ→0, то этот предел называется определенным интегралом от функции f(x) по отрезку [a, b] и обозначается следующим образом:

В этом случае функция f(x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, х – переменной интегрирования.