Відстань від точки до прямої.

Нехай задана пряма L рівнянням і точка M₀(x₀;y₀) (див. рис. 25). Потрібно знайти відстань від точки М₀ до прямій L.

рис. 25.

Розв’язок: Відстань d, від точки М₀ до прямою L рівно модулю проекції вектора , де M₁(x₁;y₁) - довільна точка прямої L, на напрям нормального вектора . Отже

.

Оскільки точка M₁(x₁;y₁) належить прямою L, то, тобто . Тому

(2.13)

що і потрібно було отримати.

Різні види рівнянь прямої в просторі. Взаємне розміщення прямих в просторі.

Рівняння прямої у тривимірному просторі також записується багатьма способами.

Пряму як перетин двох площин задають системою лінійних рівнянь

. (2.11)

Симетричне (канонічне) рівняння прямої, що проходить через точку (x₀;y₀;z₀) паралельно до напрямного вектора , має вигляд

. (2.12)

Параметричне рівняння прямої є таким:

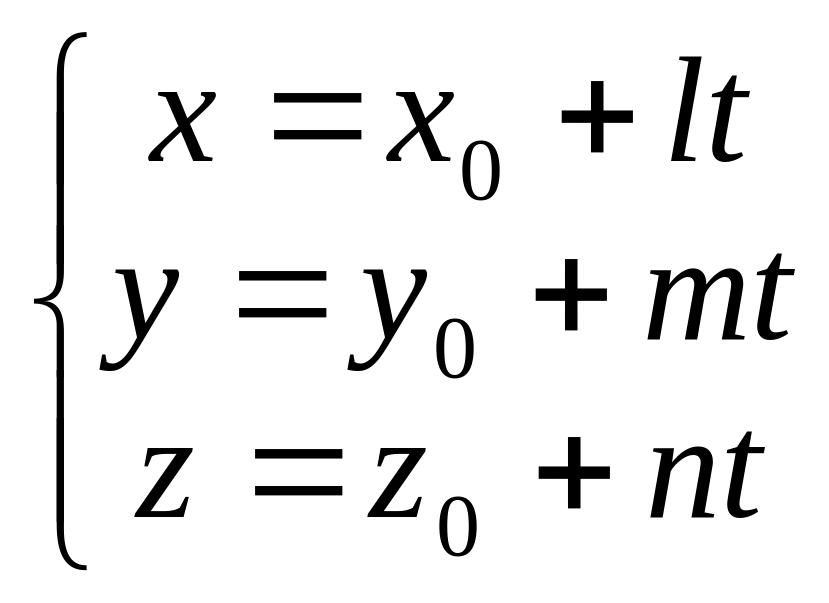. (2.13)

Рівняння прямої в просторі, яка проходить через дві точки (x₁;y₁;z₁) та (x₂;y₂;z₂) , є подібним до рівняння прямої на площині:

. (2.14)

Приклад. Пряма в просторі проходить через дві точки: M₁(1;2;3) та M₂(4;6;8) . Рівнянням цієї прямої згідно (2.14) є рівняння

.

Виконавши операції віднімання, отримуємо канонічне рівняння

.

Від останнього рівняння перейдемо до параметричного задання прямої (формула 2.13): .

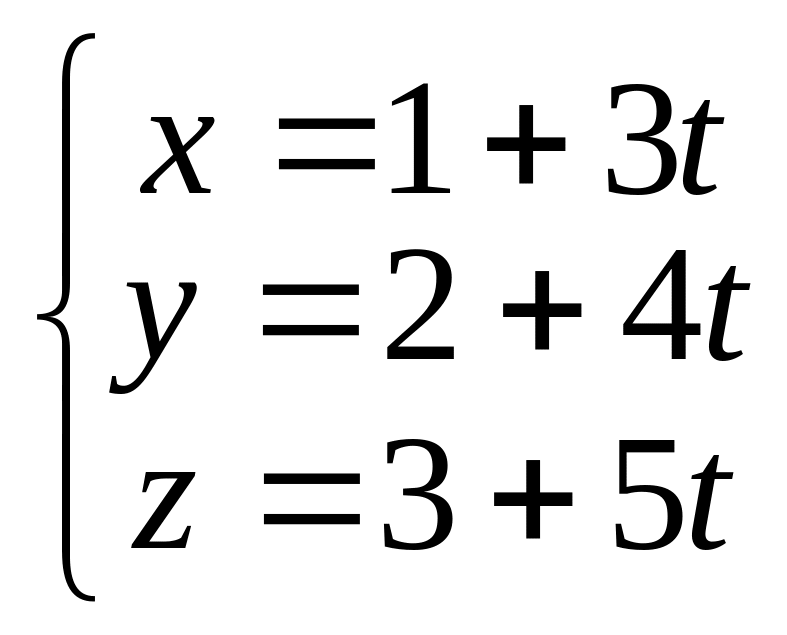У тривимірному просторі справджуються такі формули для кутів:

кут між двома прямими та

обчислюється згідно з формулою ;

кут між прямою та площиною Ax+By+Cz+D=0 знаходиться за формулою .

Рівняння площини, що проходить через три задані точки. Рівняння площини у відрізках на осях.

У просторі із заданою декартовою системою координат однозначне розташування площини можна задати різними способами, відповідно існують різні рівняння площини в просторі.

1.     Рівняння площини, що проходить через три задані точки

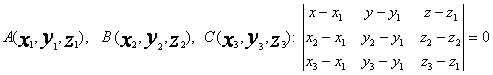
Тут x, у, z – поточні координати точки площини.

2.     Рівняння площини, що проходить через задану точку М (x₀, y₀, z₀) перпендикулярно заданому вектору

3.     Якщо в рівнянні розкрити дужки і позначити вільний член через D, то отримаємо загальне рівняння площини:

Ax + By + Cz + D = 0

Якщо в загальному рівнянні один з коефіцієнтів А, В, С рівний нулю, то площина проходить паралельно відповідній осі. Якщо два коефіцієнти з А, В, С рівні нулю, площина паралельна одній з координатної площини. Наприклад, площина 4x – 5z – 1 = 0 проходить паралельно осі Оу, площина у + 3 = 0 проходить паралельно координатній площині xOz через крапку у = -3 на осі Оу.

Коефіцієнти А, В, С в загальному рівнянні є одночасно компонентами вектора, перпендикулярного площині.

4.     Розділивши рівняння на (-D), отримаємо рівняння площини у відрізках:

Тут а, b, с – відрізки, що відсікаються площиною на осях координат. Наприклад, площина

перетинає осі координат в точках х = 2, у = -3, z = 1.

Взаємне розміщення прямої і площини

в просторі

Диференціальне числення.

Числова послідовність.

Границя числової послідовності

Частковим, проте важливим для математичної теорії видом функції дійсної змінної є числові послідовності.

Означення 1.1. Числовою послідовністю називається функція дійсної змінної, областю визначення якої є множина натуральних чисел.

Отже, числова послідовність є заданою, якщо кожному натуральному числу  за певним правилом поставлено у відповідність дійсне число . Розрізняють два найпоширеніші способи задання числових послідовностей: а) аналітичний спосіб, коли послідовність задається формулою загального члена , що виражає  через номер ; б) рекурентний спосіб (від лат. recursio – повернення), коли -й член послідовності виражається через комбінацію її попередніх членів. Наприклад, вирази    задають послідовності аналітичним способом. Правило ,       ,       – рекурентний спосіб задання послідовності. У такому разі так задаються числа Фібоначчі. Розглянемо числову послідовність, задану загальним членом . Зобразимо її члени точками числової осі (рис. 1). 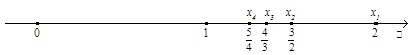Рис. 1. Зображення членів послідовності на числовій осі

Легко помітити, що із зростанням  члени послідовності  як завгодно близько наближаються до 1. Із збільшенням    зменшується: Крім того, для довільного як завгодно малого числа  ми завжди можемо вказати такий номер  елемента послідовності, починаючи з якого . Наприклад, На цих міркуваннях ґрунтується означення границі послідовності.

Означення 1.2. Число  називається границею послідовності , якщо для довільного додатного числа  можна вказати номер  такий, що для кожного натурального числа  виконується нерівність .

Те, що число  є границею послідовності  записується так:  або , якщо . Якщо послідовність має границю, то вона називається збіжною, якщо ні – розбіжною. Те, що , геометрично означає, що яким би малим не було число , всі члени послідовності  з номерами  будуть знаходитися всередині -околу точки  (рис. 2)

Рис. 2. Графічне зображення збіжної послідовності