
- •Вступ до теорії функції комплексного змінного. Тригонометрична і показникова форми комплексних чисел.
- •Дії над комплексними числами заданими в тригонометричній і показниковій формі
- •Загальний висновок про квадратні рівняння
- •Елементи лінійної алгебри. Визначники вищих порядків.
- •Обчислення визначників вищих порядків.
- •Ранг матриці.
- •Обернена матриця.
- •Знайти матрицю, обернену до матриці і перевірити, чи справджуються рівності .
- •Системи лінійних рівнянь. Умови сумісності систем лінійних рівнянь. Теорема Кронекера-Капеллі. Основні визначення
- •Формули Крамера.
- •Метод Гауса.
- •Матричний запис системи лінійних рівнянь і її розв’язування.
- •Аналітична геометрія. Системи координат. Вектори. Лінійні операції над векторами
- •Довжину вектора будемо позначати таким чином:
- •Додавання векторів.
- •Поняття про лінію та її рівняння.
- •Відстань від точки до прямої.
- •Різні види рівнянь прямої в просторі. Взаємне розміщення прямих в просторі.
- •Рівняння площини, що проходить через три задані точки. Рівняння площини у відрізках на осях.
- •Властивості числових границь мають вигляд:
- •Основні теореми про границі
- •Урахуємо, що , а функція є обмеженою. Визначні границі.
- •Неперервність функції на відрізку. Властивості.
- •1. Неперервність функції в точці і на відрізку
- •2. Класифікація розривів функції
- •3. Властивості неперервних функцій та дії з ними
- •Задачі, що приводять до поняття похідної. Означення похідної. Її геометричний та механічний зміст. Дотична до кривої.
- •Означення похідної
- •Геометричний зміст похідної
- •Механічний зміст похідної
- •Рівняння дотичної і нормалі до плоскої кривої
- •Залежність між неперервністю та диференційованістю функції. Правила диференціювання. Похідні основних елементарних функцій.
- •Основні правила диференціювання
- •Похідні від основних елементарних функцій
- •Монотонність функції. Екстремум функції
- •Зразки розв’язування задач
- •Означення диференціала функції однієї змінної. Правила знаходження диференціалу.
- •Правила диференціювання:
- •Диференціал складеної функції. Інваріантність форми диференціалу.
- •Зауваження
- •Інваріантність форми першого диференціала
- •Приклад 1
- •Застосування диференціалу до наближених обчислень
- •Теореми Ферма і Ролля, Коші і Лагранжа.
- •Формула Тейлора.
- •Функції багатьох змінних. Множини точок на площині
- •Основні поняття та означення функції багатьох змінних. Способи задання функції. Область визначення. Графіки. Лінії рівня.
- •Похідна за напрямом. Градієнт.
- •Частинні похідні та диференціали вищих порядків.
- •Неявні функції. Похідні неявних функцій.
- •Поняття умовного екстремума.
- •Прямий метод знаходження точок умовного екстремума (метод включення).
- •Метод Лагранжа знаходження точок умовного екстремума. Метод найменших квадратів.
- •Метод найменших квадратів
- •Знаходження найбільшого та найменшого значень неперервної функції на замкненій обмеженій множині
- •Інтегральне числення. Первісна. Невизначений інтеграл.
- •Зразки розв’язування задач
- •Інтегрування раціональних дробів, тригонометричних та ірраціональних функцій.
- •Зразки розв’язування задач
- •Інтегрування функцій, раціонально залежних від тригонометричних
- •Зразки розв’язування задач
- •Інтегрування деяких іраціональних функцій
- •Зразки розв’язування задач
- •Деякі інтеграли, що не виражаються через елементарні функції
- •Визначений інтеграл із змінною верхньою межею. Теорема Ньютона-Лейбніца.
- •Зразки розв’язування задач
- •Наближене обчислення визначеного інтеграла. Формули прямокутників і трапеції.
- •Невласні інтеграли. Поняття про подвійний інтеграл. Зведення подвійного інтеграла до повторного. Невласні інтеграли першого роду (з нескінченими межами)
- •Ознаки збіжності невласних інтегралів першого роду
- •Зразки розв’язування задач
- •Диференціальні рівняння. Наближені методи розв’язування диференціальних рівнянь.
- •Однорідні диференціальні рівняння
- •Диференціальні рівняння у повних диференціалах
- •1. Загальна теорія
- •2. Множник, що Інтегрує
- •Зниження порядку деяких диференціальних рівнянь другого порядку
- •Рівняння вигляду .
- •Зразки розв’язування задач
- •Ряди. Достатні ознаки збіжності для рядів з додатними членами. Використання ознак збіжності рядів з додатними членами.
- •Знакозмінні ряди. Абсолютна та умовна збіжність знакозмінних рядів.
- •Знакопочергові ряди. Ознака Лейбніца.
- •Зразки розв’язування задач
- •Степеневі ряди. Інтервал і радіус збіжності степеневого ряду.
- •Зразки розв’язування задач
- •Диференціювання та інтегрування степеневих рядів.
- •Ряди Тейлора і Маклорена.
- •Застосування рядів для наближених обчислень.
Довжину вектора будемо позначати таким чином:
![]() .
.
Додавання векторів.
Щ
Рис. 3.1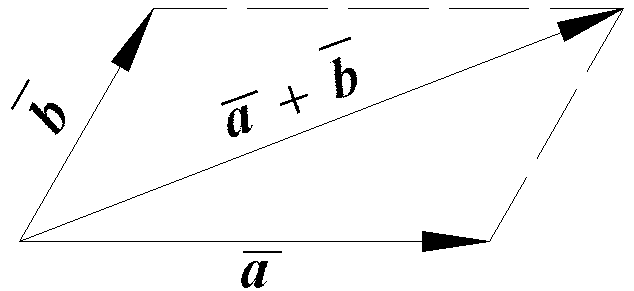
![]() і
і
![]() ,
треба відкласти ці вектори від довільної
точки та побудувати на них паралелограм.
Сумою векторів буде діагональ, що
виходить з початку векторів
і
(рис. 3.1).
,
треба відкласти ці вектори від довільної
точки та побудувати на них паралелограм.
Сумою векторів буде діагональ, що
виходить з початку векторів
і
(рис. 3.1).
Цей спосіб побудови називається правилом паралелограма.
Суму двох векторів можно побудувати ще й за правилом трикутника.
В
Рис. 3.2
![]() від кінця вектора
від кінця вектора
![]() .
Сумою векторів
і
буде вектор, що з’єднує початок
з кінцем
(рис. 3.2).
.
Сумою векторів
і
буде вектор, що з’єднує початок
з кінцем
(рис. 3.2).
Щ
Рис. 3.3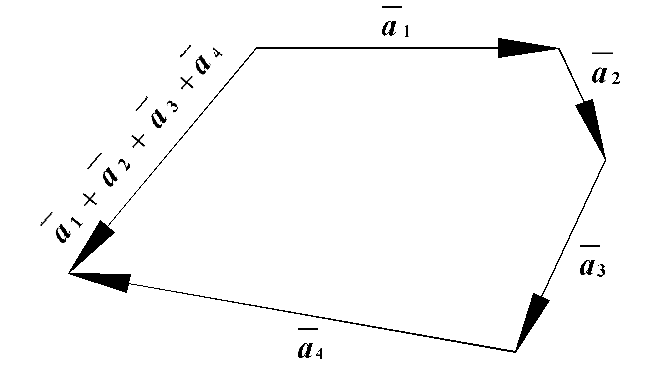
![]() ,
треба від довільної точки відкласти
,
треба від довільної точки відкласти
![]() ,
потім від його кінця відкласти
,
потім від його кінця відкласти
![]() і т.д., нарешті від кінця
і т.д., нарешті від кінця
![]() відкласти
відкласти
![]() .
Сумою векторів буде
вектор, напрямлений від початку
до кінця
(рис. 3.3).
.
Сумою векторів буде
вектор, напрямлений від початку
до кінця
(рис. 3.3).
Віднімання векторів.
Щ
Рис. 3.4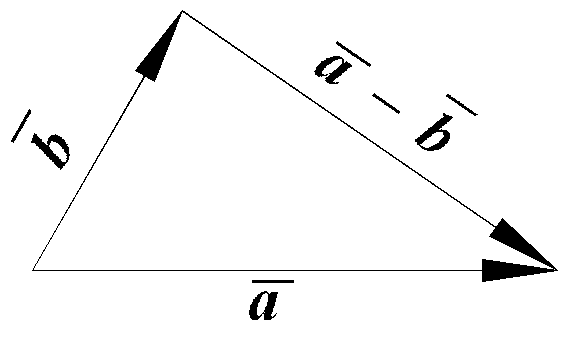
![]() ,
треба відкласти ці вектори від довільної
точки, з’єднати їх кінці та вибрати на
цьому відрізку напрямок від кінця
до кінця
(рис. 3.4).
,
треба відкласти ці вектори від довільної
точки, з’єднати їх кінці та вибрати на
цьому відрізку напрямок від кінця
до кінця
(рис. 3.4).
Множення вектора на число.
Добутком ненульового
вектора
на число k
називається вектор, який має напрям
вектора
,
якщо
![]() ,
і протинапрям, якщо
,
і протинапрям, якщо
![]() (при
(при
![]() ,
,
![]() ).
).
Ці три операції називаються лінійними операціями з векторами.
Проекція вектора на вісь.
П
Рис. 3.5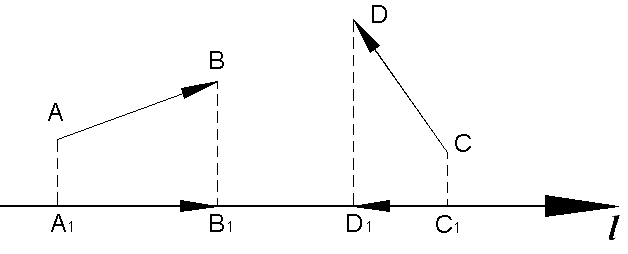
![]() ,
,
![]() .
.
Властивості проекції.
 ;
;
б)
![]() ;
;
в)
![]() .
.
Прямокутна система координат.
Нехай у просторі
задано три попарно перпендикулярні осі
OX, OY, OZ.
Координатами
вектора
![]() на осі називаються проекції вектора
на ці осі:
на осі називаються проекції вектора
на ці осі:
![]() ,
,
![]() ,
,
![]() .
.
Якщо
![]() -
одиничні вектори, що напрямлені по OX,
OY, OZ, то
-
одиничні вектори, що напрямлені по OX,
OY, OZ, то
![]() .
.
Якщо
![]() ,
,
![]() то координати вектора
то координати вектора
![]() .
.
Правила дій над векторами, заданими своїми координатами.
Якщо
![]() ,
,
![]() ,
то
,
то
![]() ;
;
![]() ;
;
![]() .
.
Довжина вектора. Напрямлені косинуси вектора.
![]() ;
;
![]() ;
; ![]() ;
; ![]() ,
,
де
![]() -
кути між
та осями OX,
OY, OZ.
-
кути між
та осями OX,
OY, OZ.
Для напрямлених конусів справедливо співвідношення:
![]()
Поділ відрізка в даному відношенні.
Нехай точки А, В мають координати , .
Якщо відрізок АВ
поділимо точкою М
у відношенні:
![]() ,
то координати точки М
знаходять за формулами:
,
то координати точки М
знаходять за формулами:
![]() ;
; ![]()
![]() .
.
Якщо
![]() ,
то отримуємо формули для знаходження
координат середини відрізка.
,
то отримуємо формули для знаходження
координат середини відрізка.
Поняття про лінію та її рівняння.
Лінія на площині розглядається (задається) як множина точок, що має певні і притаманні тільки їм геометричні властивості. Наприклад, коло радіусом R це безліч всіх точок площини, віддалених на відстань R від деякої фіксованої точки О (центра кола).
Введення на площині системи координат дозволяє визначати положення точки площини завданням двох чисел — її координат, а положення лінії на площині визначається за допомогою рівняння (тобто рівність, що зв'язує координати точок лінії).
Рівняння лінії (або кривої) на площині Оху називається таке рівняння F(х;у)=0 з двома змінними, якому задовольняють координати х і у кожної точці лінії і не задовольняють координати будь-якої точки, які не лежать на цій лінії.
Змінні x і у в рівнянні лінії називаються поточними координатами точок лінії.
Рівняння лінії дозволяє вивчення геометричних властивостей лінії замінити дослідженням його рівняння.
Так, для того, щоб встановити чи лежить точка A(x0; y0) на даній лінії, досить перевірити (не вдаючись до геометричних побудов), чи задовольняють координати точки А рівнянню цієї лінії у вибраній системі координат.
Приклад:
Чи
лежать точки К(—2;
1)
і
L(1;
1)
на лінії
![]() ?
?
○ Підставивши
в рівняння замість xіу
координати
точки К,
отримаємо
![]() .
Отже, точки К
лежить
на даній лінії. Точка L
не
лежить на даній лінії, оскільки
.
Отже, точки К
лежить
на даній лінії. Точка L
не
лежить на даній лінії, оскільки
![]() .●
.●
Завдання про знаходження точок перетину двох ліній, заданих рівняннями F1(х; у)=0 і F2(х; у)=0, зводиться до відшукування точок, координати яких задовольняють рівняння обох ліній, тобто зводиться до розв’язку системи двох рівнянь з двома невідомими:
Якщо ця система не має дійсних розв’язок, то лінії не перетинаються.
Аналогічним чином вводиться поняття рівняння лінії в полярній системі координат.
Рівняння
F(![]() ;
;![]() )=0
називається рівнянням
даної лінії в полярній системі
координат,
якщо
координати будь-якої точки, лежать на
цій лінії,
і лише вони, задовольняють це рівняння.
Пряму на
площині можна задати за допомогою двох
рівнянь:
)=0
називається рівнянням
даної лінії в полярній системі
координат,
якщо
координати будь-якої точки, лежать на
цій лінії,
і лише вони, задовольняють це рівняння.
Пряму на
площині можна задати за допомогою двох
рівнянь:
![]() (2.1)
(2.1)
де х і у — координати довільної точки М(х; у), які лежать на даній лінії, а t — змінна, називається параметром; параметр t визначає положення точки (х; у) на площині.
Наприклад,
якщо
![]() ,
,
![]() у,
то
значенню
параметра
у,
то
значенню
параметра
![]() відповідає на
площині точка з координатами (3;
4),
оскільки
відповідає на
площині точка з координатами (3;
4),
оскільки
![]() ,
,
![]() .
.
Якщо параметр t змінюється, то точка на площині переміщається, описуючи дану лінію. Такий спосіб завдання прямої називається параметричним, а рівняння (2.1) — параметричними рівняннями лінії.
Щоб
перейти від параметричних рівнянь лінії
до рівняння виду F(х;у)=0,
треба яким-небудь чином з двох рівнянь
виключити параметр t.
Наприклад, від параметричних рівнянь
![]() шляхом
підстановки
шляхом
підстановки
![]() в
друге рівняння, легко отримати рівняння
в
друге рівняння, легко отримати рівняння
![]() або
або
![]() ,
тобто виду F(х;
у)= 0.
Проте, відмітимо, такий перехід не завжди
доцільний і не
завжди можливий.
,
тобто виду F(х;
у)= 0.
Проте, відмітимо, такий перехід не завжди
доцільний і не
завжди можливий.

рис. 9.
Лінію
на площині можна задати векторним
рівнянням,
де t
— скалярний змінний параметр. Кожному
значенню t0
відповідає певний вектор![]() площини.
При зміні параметра t
кінець вектора
площини.
При зміні параметра t
кінець вектора
![]() опише деяку лінію (див. рис.
9).
опише деяку лінію (див. рис.
9).
Векторному рівнянню лінії в системі координат Оху відповідають два скалярні рівняння (2.1), тобто рівняння проекцій на осі координат векторного рівняння лінії є її параметричні рівняння.
Векторне рівняння і параметричне рівняння лінії мають механічний сенс. Якщо точка переміщається на площині, то вказані рівняння називаються рівняннями руху, а пряма — траєкторією точки, параметр t при цьому є час.
Отже, всякій лінії на площині відповідає деяке рівняння виду F(х; у)= 0.
Всякому
рівнянню виду F(х;
у)= 0
відповідає, взагалі кажучи, деяка лінія,
властивості якої визначаються даним
рівнянням (вираз «взагалі кажучи»
означає, що сказане допускає виключення.
Так,
рівнянню (х-2)2+(у-3)2=0
відповідає не лінія, а точка (2;3);
рівнянню
![]() на площині не відповідає ніякий
геометричний
образ).
на площині не відповідає ніякий
геометричний
образ).
У аналітичній геометрії на площині виникають два основні завдання. Перше: знаючи геометричні властивості кривої, знайти її рівняння; друге: знаючи рівняння кривої, вивчити її форму і властивості. На малюнках 10-18 приведені приклади деяких кривих і вказані їх рівняння.
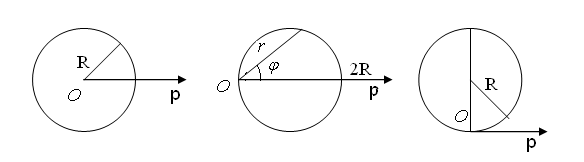
![]()
![]()
![]()
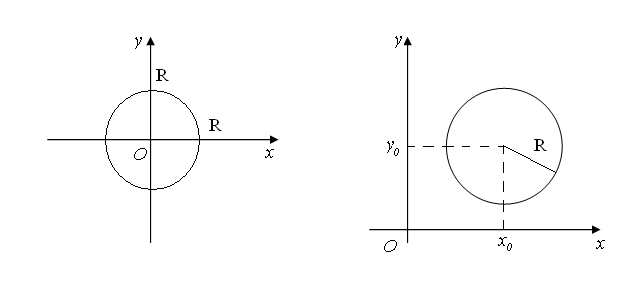
![]() або
або
![]()
![]()
рис. 10. Коло радіусом R
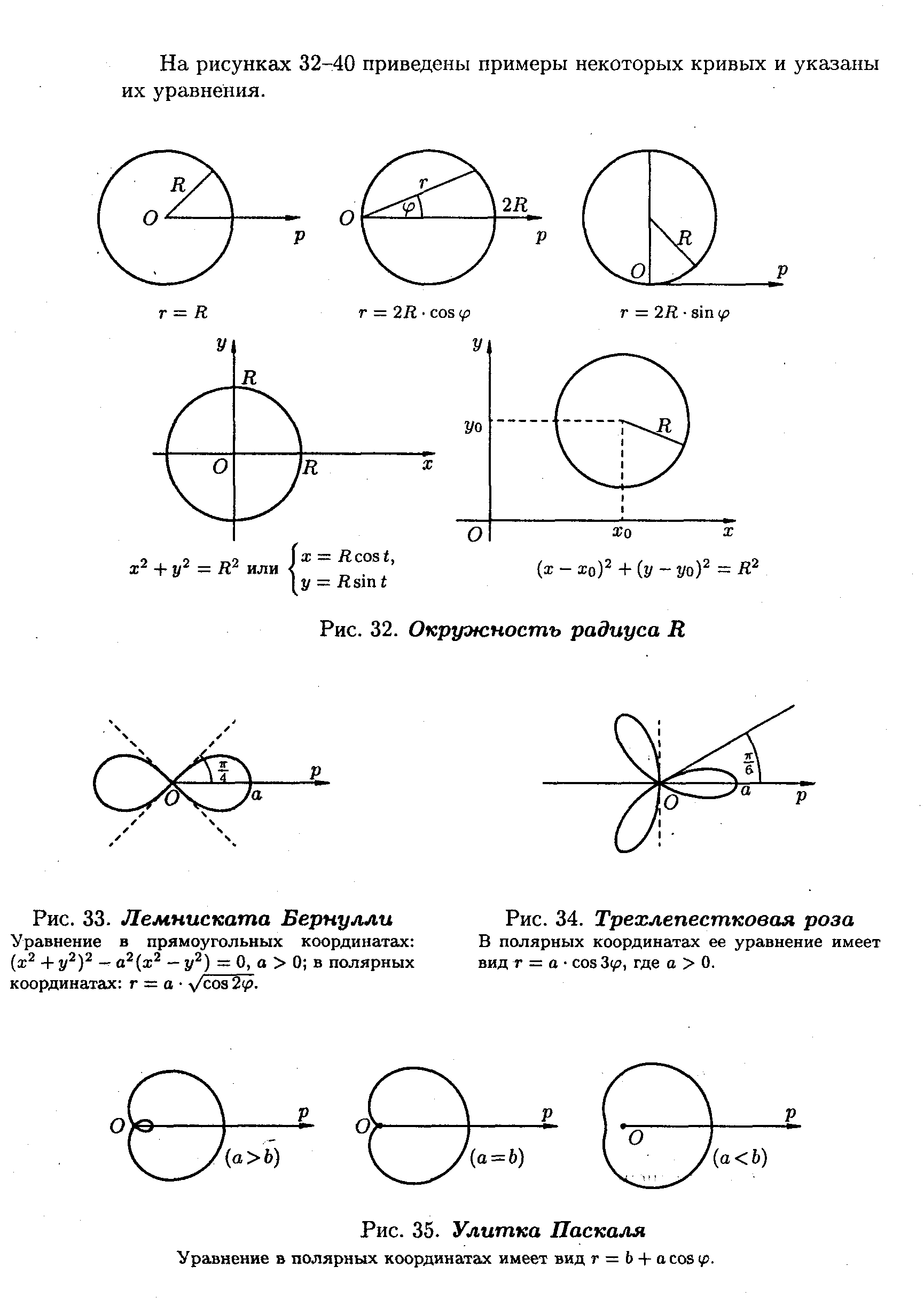
рис.
11.
Лемніската
Бернуллі рис.
12.
Трьохпелюсткова
роза
Рівняння
в прямокутних координатах:
У
полярних координатах її рівняння
(х2+у2)2–![]() 2(х2–у2)=0,
>
0;
має
вигляд,
2(х2–у2)=0,
>
0;
має
вигляд,
![]() де
>0.
де
>0.
у полярних
координатах:
![]() .
.
рис. 13. Равлик Паскаля
Рівняння
в полярних координатах має вигляд
![]() .
.
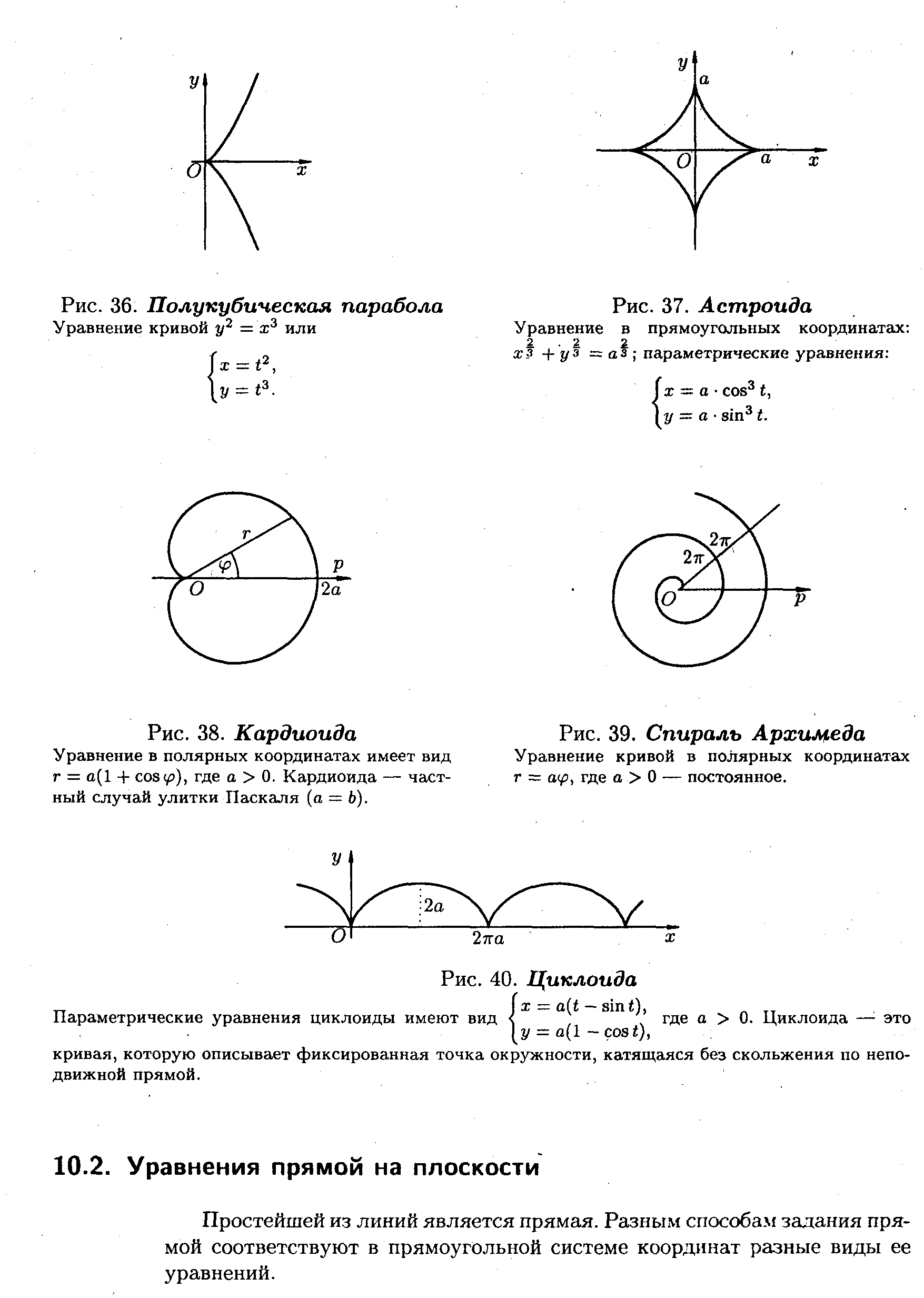
рис. 14. Напівкубічна парабола рис. 15. Астроїда
Рівняння
кривої у2
=
х3
або Рівняння
в прямокутних координатах: ![]() ;
параметричні рівняння:
;
параметричні рівняння:
![]()
![]()
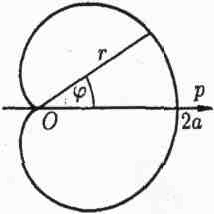

рис. 16. Кардіоїда рис. 17. Спіраль Архімеда
Рівняння в полярних координатах рівняння кривої в полярних
має
вигляд![]() ,
координатах,
,
координатах,
![]()
де
![]() .
Кардіоїда
—
окремий
випадок де
- постійне.
.
Кардіоїда
—
окремий
випадок де
- постійне.
равлика
Паскаля (![]() ).
).

рис. 18. Циклоїда
Параметричні
рівняння циклоїди мають вигляд
![]() де
а > 0.
де
а > 0.
Циклоїда — це крива, яку описує фіксована точка кола, що котиться без ковзання по нерухомій прямій.
Кут між двома прямими. Умови паралельності і перпендикулярності двох прямих
Нехай
прямі L1
і L2
задані рівняннями з кутовими коефіцієнтами
![]() і
і
![]() (див.
рис.
24).
(див.
рис.
24).
П отрібно
знайти кут,
на
який треба повернути в позитивному
напрямі пряму L1
навколо точки їх перетину до збігу з
прямій L2.
отрібно
знайти кут,
на
який треба повернути в позитивному
напрямі пряму L1
навколо точки їх перетину до збігу з
прямій L2.
○ Маємо
рис. 24.![]() (теорема про зовнішній кут трикутника)
або
(теорема про зовнішній кут трикутника)
або
![]() .
Я
.
Я![]() ,
то
,
то
![]() .
.
Але
![]() ,
,
![]() ,
тому
,
тому
![]() , (2.12)
, (2.12)
звідки легко отримаємо величину шуканого кута.
Якщо
потрібно обчислити гострий кут між
прямими,
не враховуючи, яка пряма є першою, яка
— другою, то права
частина формули (2.12) береться по модулю,
тобто
![]() .
.
Якщо
прямі
L1
і L2
паралельні, то
![]() і
і
![]() .
З формули (2.12) виходить
.
З формули (2.12) виходить
![]() ,
тобто
,
тобто
![]() .
і навпаки, якщо прямі L1
і L2
такі, що
,
то прямі паралельні. Отже, умовою
паралельності два прямих є рівність їх
кутових коефіцієнтів:
.
.
і навпаки, якщо прямі L1
і L2
такі, що
,
то прямі паралельні. Отже, умовою
паралельності два прямих є рівність їх
кутових коефіцієнтів:
.
Якщо
прямі L1
і
L2
перпендикулярні,
то
![]() .
Отже
.
Отже
![]() .
Звідси, тобто
.
Звідси, тобто
![]() (або )
(або )
![]() .
Справедливо
і зворотне твердження. Таким чином,
умовою перпендикулярності прямих є
рівність
.●
.
Справедливо
і зворотне твердження. Таким чином,
умовою перпендикулярності прямих є
рівність
.●
