Системи лінійних рівнянь. Умови сумісності систем лінійних рівнянь. Теорема Кронекера-Капеллі. Основні визначення

Системою m лінійних рівнянь з n змінними x₁, x₂, …, x_n називається система, яка має наступний вигляд:

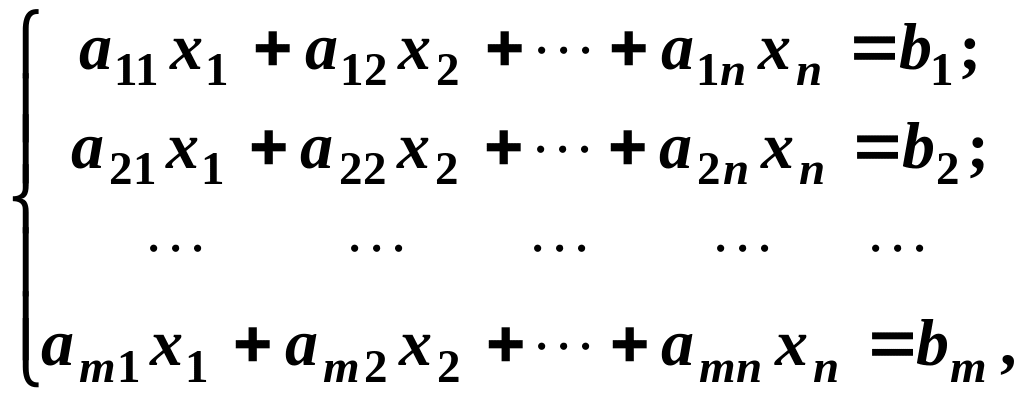
де а_ij – коефіцієнти при змінних; b_i - вільні члени,

Упорядкована сукупність чисел , називається розв’язком системи, якщо при заміні х₁ на а₁ , х₂ на а₂ , … , х_n на а_n у кожному рівнянні системи дістанемо n правильних числових рівностей.

Система, що має розв’язок, називається сумісною. Система, яка не має жодного розв’язку, називається несумісною. Система з єдиним розв’язком називається визначеною, а з більшим числом розв’язків – невизначаною.

Система двох лінійних рівнянь з двома змінними має вигляд:

(2.1)

а систему трьох лінійних рівнянь з трьома змінними записують у

вигляді:

Система рівнянь називається однорідною, якщо всі вільні члени дорівнюють нулю, і неоднорідною, якщо хоч один з них відмінний від нуля.

Множина чисел аіа2,...,а_п називається впорядкованою, якщо вказані порядок слідування цих чисел, яке з них є першим, яке другим, яке третім...

Упорядкований набір п чисел називається розв'язком системи , якщо при підстановці цих чисел замість невідомих х₁ х₂, х_п

рівняння системи перетворюються у тотожні. Таку систему чисел називають також n-вимірним вектором, або точкою n-вимірного простору.

Система рівнянь називається сумісною, якщо вона має хоч один розвязок, і несумісною , якщо вона не має жодного розв'язку.

Сумісна система називається визначеною , якщо вона має один розв'язок.

Сумісна система називається невизначеною, якщо вона має більше ніж один розв”язок.

Дві системи лінійних рівнянь називаються еквівалентними, якщо вони мають одну множину розв'язків. Еквівалентні системи дістають внаслідок елементарних перетворень даної системи. Елементарні перетворення системи лінійних рівнянь відповідають елементарним перетворенням матриці, за умови, якщо вони виконуються над рядкам матриці.

Критерій сумісності системи лінійних рівнянь

Нехай задано систему m лінійних рівнянь з п невідомими:

а_пх_х+а_пх₂ +...+а_их_п =&,; a_2lXl+a₂₂x₂ +...+а_их_п =Ь₂₁;

С кладемо основну матрицю А і розширену матрицю А' даної системи:

Вичерпнішу відповідь про розв'язання дає теорема Кронекера Капелі.

Теорема. Для того щоб система лінійних рівнянь була сумісною необхідно і достатньо, щоб ранг її основної матриці дорівнював рангу розширеної матриці.

Якщо ранг основної матриці дорівнює рангу розширеної матриці і дорівнює числу невідомих, то система має єдиний розв 'язок.

Якщо ранг основної матриці дорівнює рангу розширеної матриці то система має безліч розв 'язків.

Приклад

Дослідити на сумісність систему рівнянь

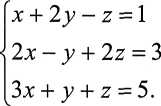
Оскільки ранг основної матриці г(А)=2, а ранг розширеної матриці г(А')=3, то задана система несумісна.

Формули Крамера.

Це правило можна застосувати, якщо кількість рівнянь і кількість невідомих співпадають. Для простоти викладу розглянемо систему трьох лінійних рівнянь з трьома невідомими ( ):

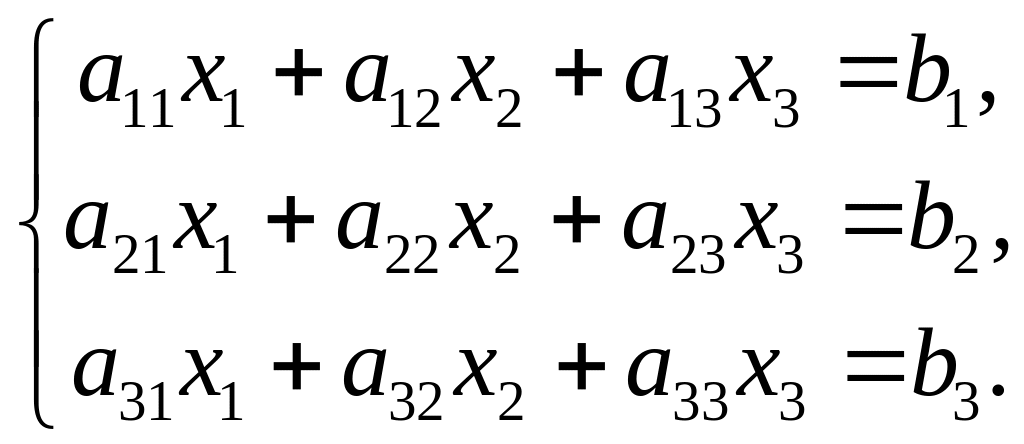(5)

Позначимо визначники:

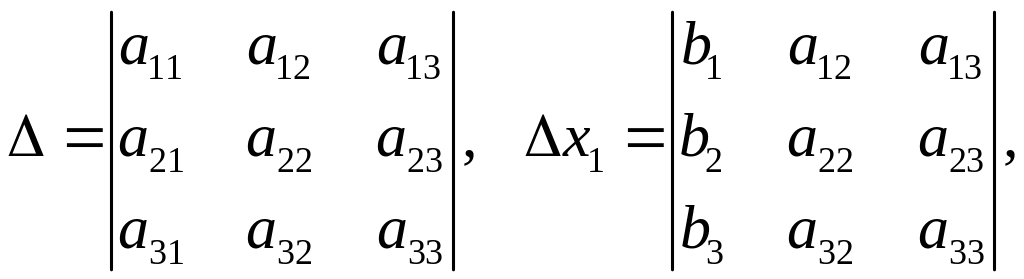
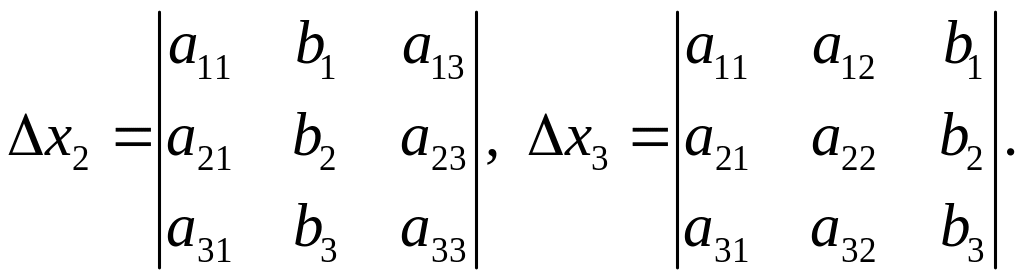
Визначник називають визначником системи і його складають з коефіцієнтів при невідомих, а у визначниках коефіцієнти при відповідних невідомих замінені вільними членами.

Якщо , то система (5) має єдиний розв’язок. Невідомі визначають за формулами

(6)

і такий спосіб визначення невідомих називають правилом Крамера.

Якщо , то система (5) має безліч розв’язків, а правило Крамера застосувати не можна.

Якщо , а хоча б один із визначників , відмінний від нуля, то система (5) несумісна.

Приклад. Розв’язати систему лінійних рівнянь методом Крамера:

Розв’язання. Складемо і обчислимо визначники:

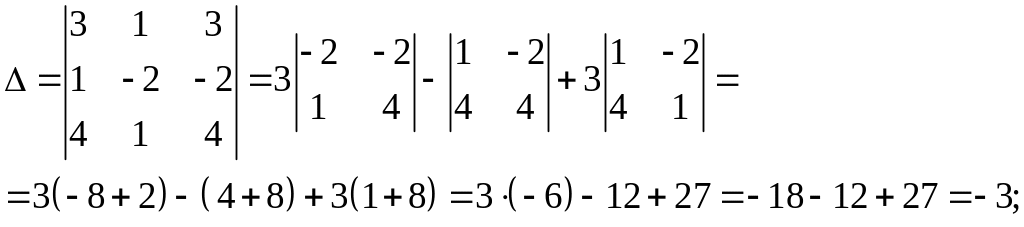
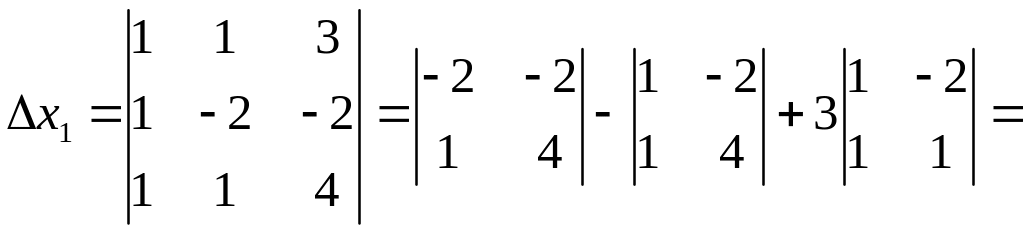
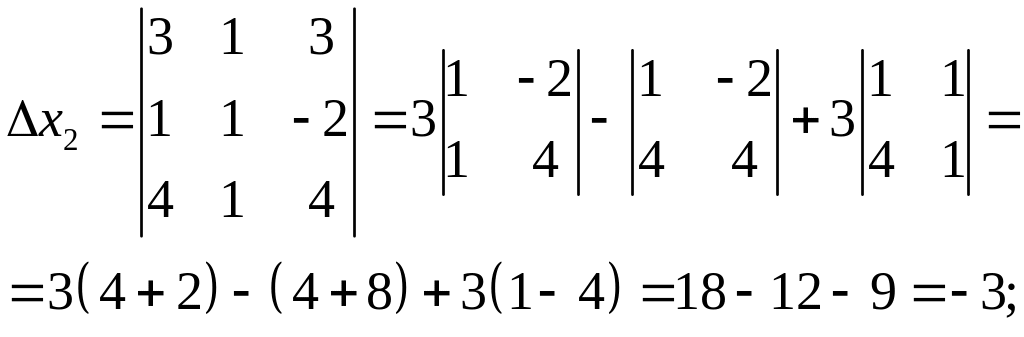
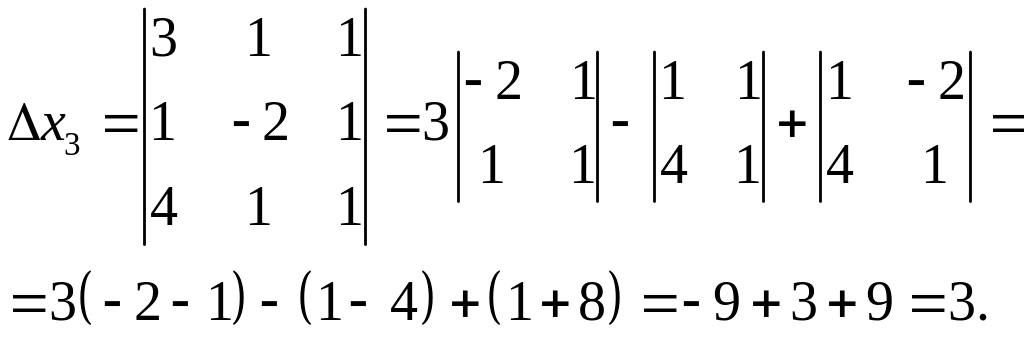
Підставимо одержані результати у формули (6). Маємо

Відповідь: .