Елементи лінійної алгебри. Визначники вищих порядків.

Теорема 1.1 (Лапласа). Визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на їх алгебраїчні доповнення.

Наприклад, для визначника третього порядку виконуються такі рівності:

 _{(розклад за елементами першого рядка);}

 (розклад за елементами другого стовпця).

Теорема 1.2. Сума добутків елементів довільного рядка (стовпця) на алгебраїчні доповнення іншого рядка (стовпця) дорівнює нулю.

Наприклад, для визначника третього порядку виконуються такі рівності:

,  .

N.B. Теореми 1.1 і 1.2 мають місце для визначників будь-якого порядку.

Розглянемо визначник n-го порядку

.

За теоремою 1.1 цей визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на їх алгебраїчні доповнення. Наприклад, розклад визначника за елементами першого рядка такий:

.

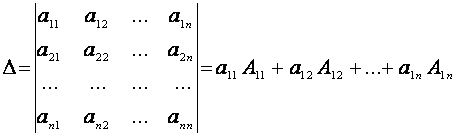Def. Визначником n-го порядку

називають алгебраїчну суму всіх можливих добутків, які містять по одному елементу з кожного рядка і кожного стовпця. Знак кожного доданка дорівнює , де  – число інверсій у других індексах за умови, що елементи (множники ) доданка розміщені в порядку зростання перших індексів. Отже,

.

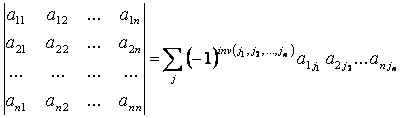Усього таких доданків n! Половину з них беруть зі знаком плюс, а іншу половину – зі знаком мінус.

N.B.Визначник n-го порядку, у якого під головною діагоналлю всі елементи нульові, дорівнює добутку елементів головної діагоналі, тобто

Обчислення визначників вищих порядків.

Визначник п порядку дорівнює сумі добутків усіх елементів будь-якого стовпця (або рядка) на відповідні їм алгебраїчні доповнення.

У випадку використання і-го рядка це правило математично виглядає так

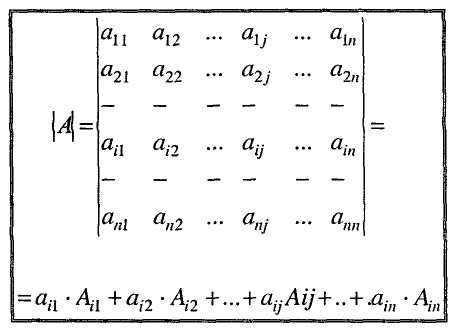
Цю рівність називають розкладом визначника за елементами і-го рядка.

Обчислення визначника п порядку зводиться до обчислення п визначників (п-1) порядку. Для скорочення обчислень визначник доцільно розкладати за елементами рядка або стовпця, який містить найбільшу кількість нулів. До нулів не треба знаходити алгебраїчних доповнень тому, що добуток 0 на його алгебраїчне доповнення дорівнює нулю. Властивості визначника дозволяють робити еквівалентні перетворення визначника і одержувати якомога більше нулів в деякому рядку або стовпці.

1. Обчисліть визначник

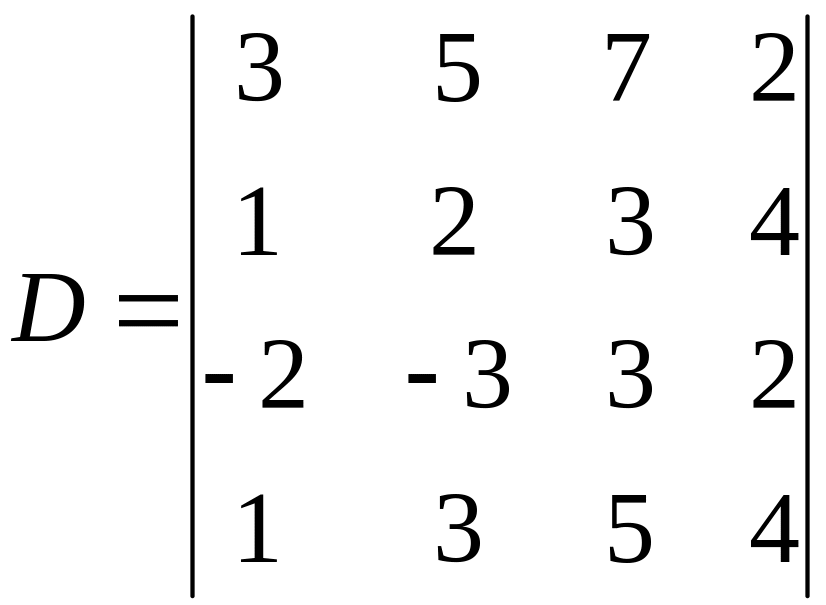
В иконаємо такі дії: 1) до елементів 1-го рядка додамо помножені на -3 відповідні елементи 2-го рядка; 2) до елементів 3-го рядка додамо подвоєні елементи 2-го рядка; 3) до елементів 4-го рядка додамо відповідні елементи 2-го рядка, помножені на -1. Тоді вихідний визначник перетвориться до вигляду.

Розклавши цей визначник по елементах 1-го стовпця, маємо

Додамо до елементів 1-го рядка елементи 3-го рядка і віднімемо від елементів 2-го рядка елементи 3-го рядка, одержимо

Розкладемо визначник по елементах 1-го стовпця.

2. Обчисліть визначник п^’ятого порядку

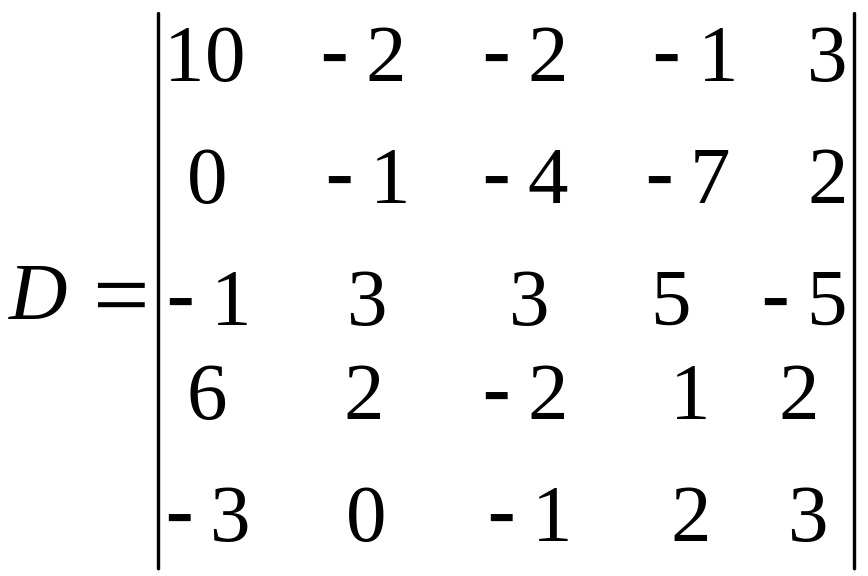
Д ля перетворення в нуль всіх елементів (крім одного) будь-якого рядка чи стовпця, вибираємо той рядок або стовпчик, який складається з найменших чисел. У визначнику таким буде другий стовпчик. Залишимо в ньому без змін елемент а₂₂=-1, а всі інші перетворимо в нулі. Для цього виконаємо:

Одержимо:

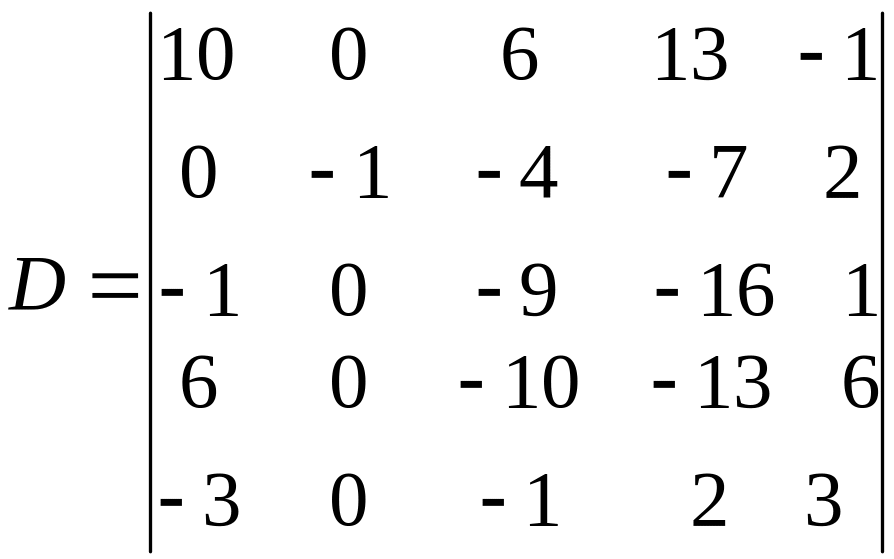
Розкладемо визначник по елементах другого стовпця.

В одержаному визначнику вже 4-го порядку з найменших елементів складається 4-ий рядок. Перетворимо в нулі всі його елементи, крім а₄₂=-1. Для цього виконаємо

(І_ст+(-3)ІІ_ст, ІІІ_ст+2 ІІ_ст, ІV_ст+3 ІІ_ст). В результаті одержимо:

Розкладемо визначник по елементах четвертого рядка

(Ми винесли за знак визначника спільний множник з елементів другого рядка і спільний множник з елементів третього рядка).

Для зменшення елементів цього визначника додамо перший стовпець до другого та третього:

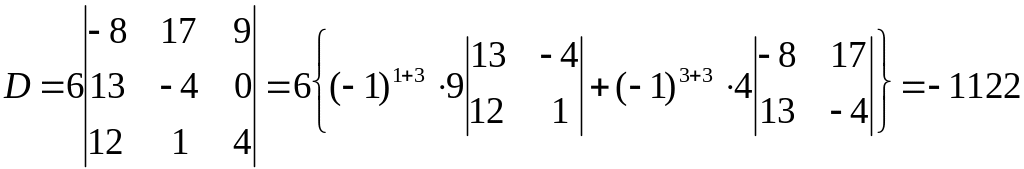
О станній визначник розклали по елементах третього стовпця.

3. Обчислити визначник n-го порядку, звівши його до трикутного вигляду:

.

Δ Віднімемо І рядок від усіх інших.

До І стовпця додамо суму всіх інших.