Похідна за напрямом. Градієнт.

Нехай функція z=f(x;y) визначена на деякому околі т. Р₀(х₀;у₀);

l - деякий промінь з початком у точці Р₀(х₀;у₀);

Р(х;у) – точка на цьому промені, яка належить околу, що розглядається

l- довжина відрізка Р₀Р.

Границя

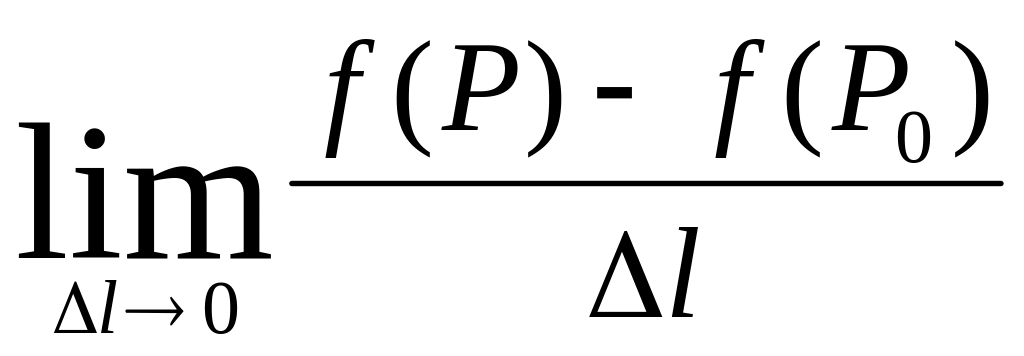, якщо вона існує, називається похідною за напрямом.

Похідна характеризує швидкість змінювання функції у точці Р₀(х₀;у₀) за напрямом .

Вектор з координатами , який характеризує напрям максимального зростання функції z=f(x;y) у точці Р₀(х₀;у₀), називається градієнтом у цій точці .

Частинні похідні та диференціали вищих порядків.

Для функцій двох та багатьох змінних , розглянемо частинні похідні.

Частинною похідною функції по одній змінній називають скінченну границю виду:

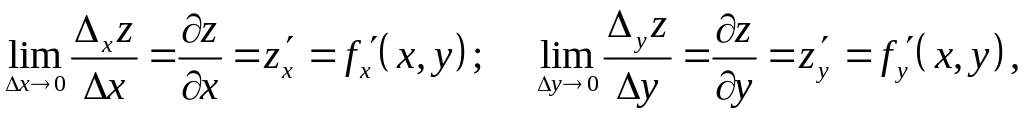
де та – частинний приріст функції по одній змінній.

Повним диференціалом функції багатьох змінних називається головна лінійна частина приросту функції. Для функції повний диференціал має вигляд

.

Повний диференціал функції багатьох змінних застосовується до наближених обчислень, вважаючи, що .

Частинні похідні знаходяться за правилами та формулами диференціювання функції однієї змінної, вважаючи решту змінних сталими величинами.

Частинною похідною n-го порядку функції багатьох змінних по одній змінній називають першу похідну від -ї похідної.

Приклад . Знайти частинні похідні другого порядку функції

.

Розв’язання. Знайдемо частинні похідні першого порядку по кожній змінній:

Від кожної частинної похідної першого порядку та знайдемо першу похідну по кожній змінній. Це будуть частинні похідні другого порядку і їх буде чотири:

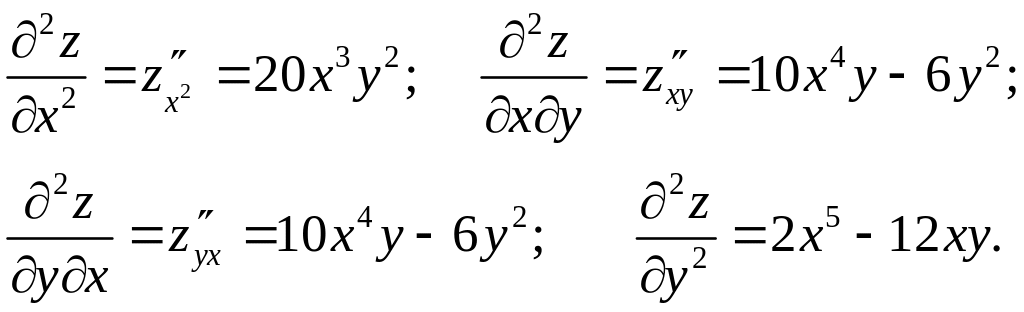
Мішані похідні, які відрізняються порядком диференціювання, , рівні між собою. Ця умова виконується у випадку їх неперервності.

Приклад . Знайти , якщо .

Розв’язання. Знайдемо частинну похідну функції тільки по або по , а потім від неї знайдемо першу похідну по іншій змінній. Одержимо

Задача. Знайти рівняння прямої методом найменших квадратів, користуючись таблицею значень

.

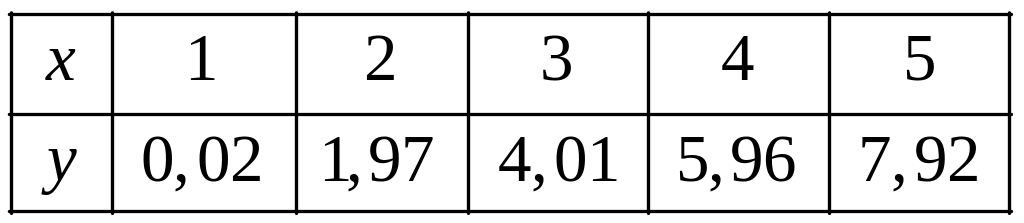Розв’язання. Згідно методу найменших квадратів для знаходження параметрів і прямої використовують систему рівнянь:

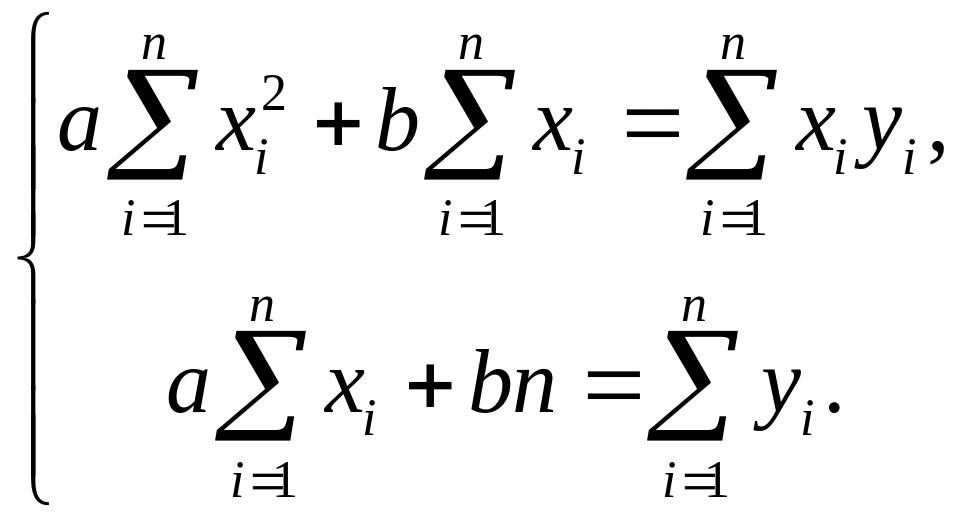(34)

Для простоти складання системи (34) складемо таблицю значень:

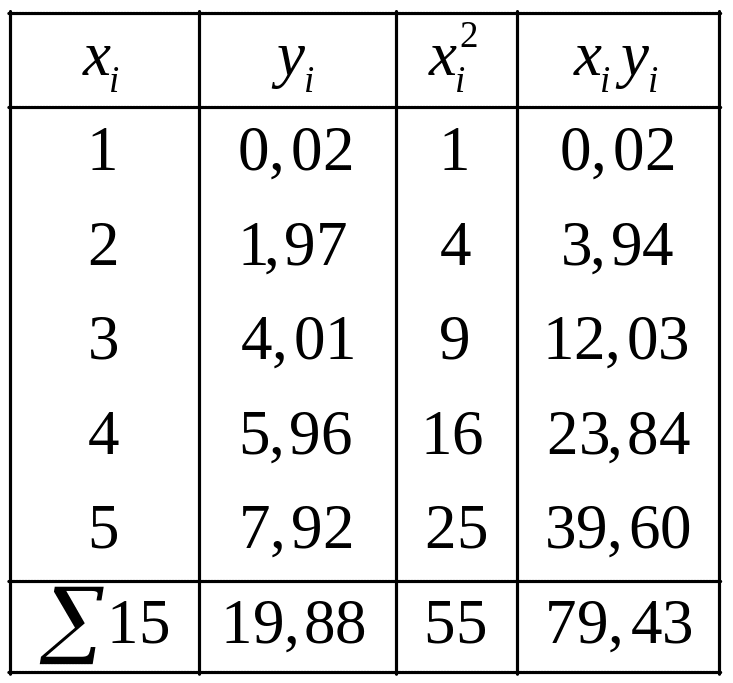
Відповідь. Рівняння прямої має вигляд .

Неявні функції. Похідні неявних функцій.

Частинні похідні неявної функції , заданої рівнянням , можуть бути обчисленні за формулами:

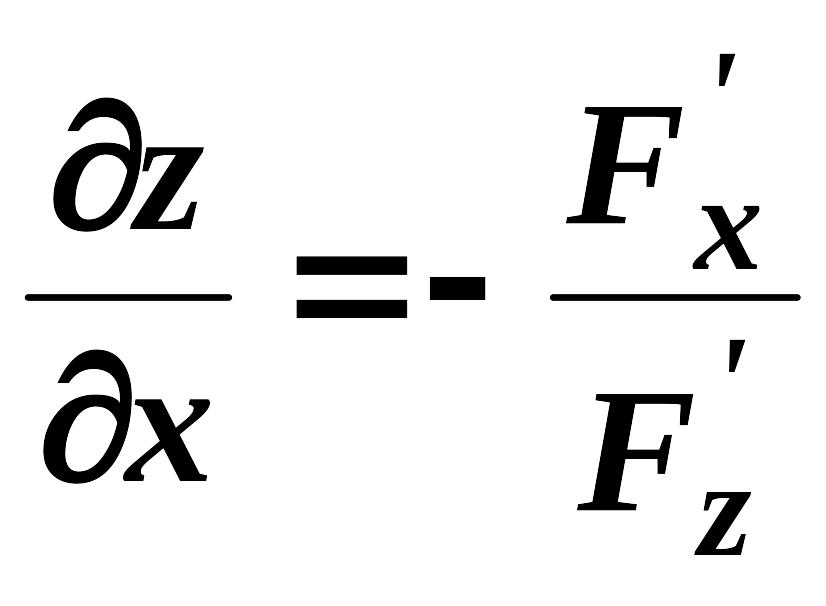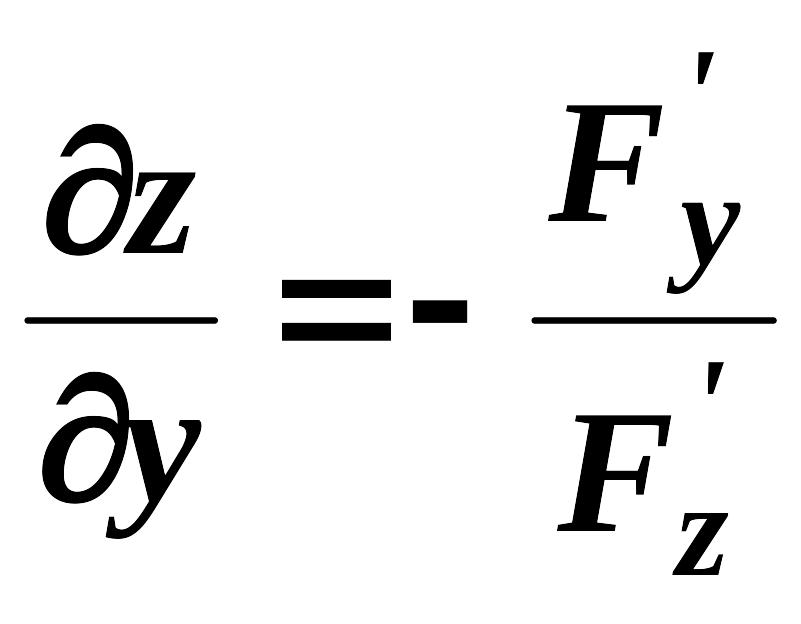, . (2.8)

Знайти похідну від функцій, заданих неявно:

а) .

.

Знайдемо частинні похідні: , .

За формулою (2.7) маємо: .

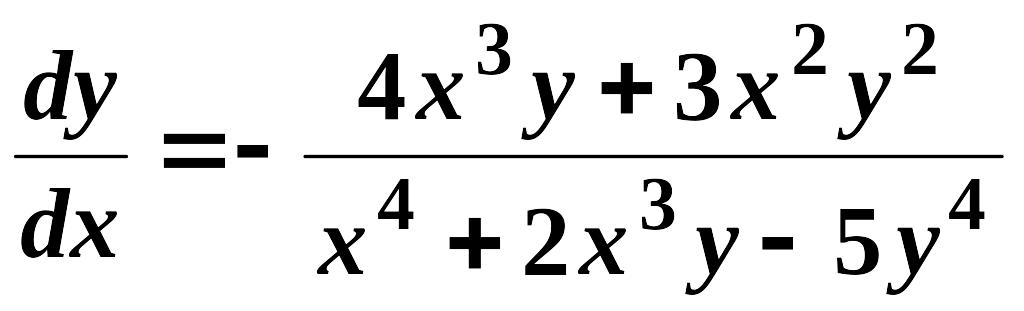б) .

.

, .

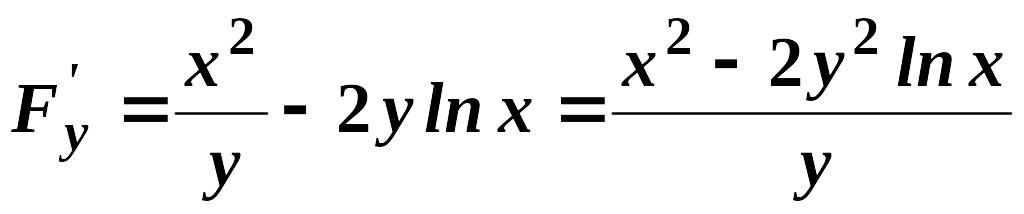За формулою (2.7) маємо: .

Нехай потрібно знайти похідну у тому випадку, коли функція задана неявно у вигляді . Узявши від функції F(x,y) повний диференціал, отримуємо

звідки .

Приклад.

Знайти похідну якщо

Маємо

звідки .