Знакопочергові ряди. Ознака Лейбніца.
План.
Означення знакопочергового ряду.
Теорема Лейбніца.
Наслідки теореми Лейбніца.
Приклади дослідження.
Рекомендована література.
Вища математика: Навч.-метод.посібник для самост.вивч.дисц./ К.Г.Валєєв та ін. – К: КНЕУ, 2002. – 606с.
Розділ 9. Тема 9.1. п.9.1.9
Дайте письмові відповіді на запитання.
Сформулюйте:
Означення знакопочергового ряду.
Теорему Лейбніца.
Степеневі ряди. Інтервал і радіус збіжності степеневого ряду.
План.
Означення степеневого ряду.
Теорема Абеля.
Інтервал і радіус збіжності степеневого ряду.
Приклади дослідження.
Рекомендована література.
Вища математика: Навч.-метод.посібник для самост.вивч.дисц./ К.Г.Валєєв та ін. – К: КНЕУ, 2002. – 606с.
Розділ 9. Тема 9.2. п.9.2.2 – 9.2.3.
Дайте письмові відповіді на запитання.
Сформулюйте:
Означення степеневого ряду.
Теорему Абеля.
Означення інтервалу і радіусу збіжності степеневого ряду.
Диференціювання та інтегрування степеневих рядів.
План.
Обґрунтування можливості почленно інтегрувати та диференціювати степеневий ряд на відрізку.
Приклади застосування.
Рекомендована література.
Вища математика: Навч.-метод.посібник для самост.вивч.дисц./ К.Г.Валєєв та ін. – К: КНЕУ, 2002. – 606с.
Розділ 9. Тема 9.2. п.9.2.4
Дайте письмові відповіді на запитання.
Обґрунтуйте можливість почленно інтегрувати та диференціювати степеневий ряд на відрізку.
Ряди Тейлора і Маклорена.
План.
Ряди Тейлора і Маклорена
Достатня умова розвинення функції в ряд Маклорена.
Необхідна і достатня умова розвинення функції в ряд Маклорена.
Приклади застосування.
Рекомендована література.
Вища математика: Навч.-метод.посібник для самост.вивч.дисц./ К.Г.Валєєв та ін. – К: КНЕУ, 2002. – 606с.
Розділ 9. Тема 9.2. п.9.2.5 – 9.2.6.
Дайте письмові відповіді на запитання.
Сформулюйте:
Достатню умову розвинення функції в ряд Маклорена.
Необхідну і достатню умову розвинення функції в ряд Маклорена.
Застосування рядів для наближених обчислень.
План.
Суть застосування рядів для наближених обчислень.
Приклади застосування рядів для наближених обчислень.
Рекомендована література.
Вища математика: Навч.-метод.посібник для самост.вивч.дисц./ К.Г.Валєєв та ін. – К: КНЕУ, 2002. – 606с.
Розділ 9. Тема 9.2. п.9.2.7
Дайте письмові відповіді на запитання.
В чому суть застосування рядів для наближених обчислень.
ТЕОРЕТИЧНИЙ МАТЕРІАЛ
(див. Додаток 1.)
ЗАВДАННЯ ДЛЯ ОБОВ’ЯЗКОВИХ ДОМАШНІХ РОБІТ
Елементи лінійної алгебри.
Завдання для ОДЗ 1
Розв’яжіть систему рівнянь всіма відомими вам способами.
Аналітична геометрія.
Завдання для ОДЗ 2
Завдання 1
Використовуючи задані координати вершин трикутника АВС , побудувати трикутник та скласти чи знайти:
– довжину сторонни АС ; загальне рівняння АС; відстань від точки В до АС
– рівняння медіани сторонни ВС у канонічній формі; кут АСВ
– рівняння прямої, що проходить через вершину В паралельно АС
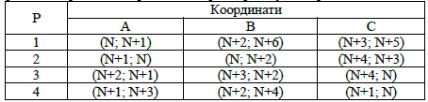
В завдані 1 значення Р та N для кожного студента визначає викладач.
