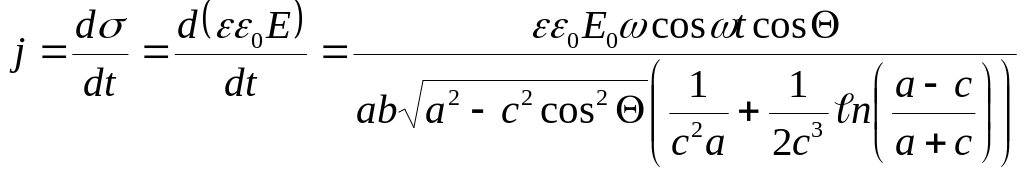2.1.4. Переменное электрическое поле.

Пусть имеется пространственно однородное электрическое поле с напряжённостью (в отсутствии тела) . Аппроксимируем тело (или сегмент тела) человека эллипсоидом вращения с большой и малой осями. Пусть вектор внешнего электрического поля направлен параллельно оси . Нормальная составляющая вектора напряжённости электрического поля на поверхности тела представляется в следующем виде:

(2.15)

где  - угол полярной ориентации рассматриваемой точки поверхности, _.

Рассмотрим случай, когда напряжённость меняется по гармоническому закону: . Тогда в теле возникает ток с плотностью

(2.16)

Напряженность магнитного поля тока и напряженность эквивалентного электрического поля определяем как :

H= jr/2; E=j

отсюда получаем:

(2.17)

Если поле носит импульсный характер, то выражение для оценки плотности потока мощности примет следующий вид:

(2.18)

2.1.5. Постоянное электрическое поле.

Если тело неподвижно в постоянном во времени и однородном, либо неоднородном по пространству электрическом поле, то поглощение энергии происходить не будет. Ток в теле возникает при его движении. Изменение поверхностной плотности зарядов на поверхности тела определяем как

,

,

где - перемещение тела в направлении градиента _{, -} диэлектрическая проницаемость окружающей тело среды. Тогда плотности тока и потока мощности составят:

	(2.19)
	(2.20)

2.2. Распределение токов в неоднородных биотканях.

Рассмотренные в предыдущем разделе математические соотношения параметров внешних и внутренних полей предполагали физическую однородность биообъекта и не учитывали различие проводимостей биологических тканей. На практике неоднородность свойств присутствует на любом иерархическом уровне организации биообъекта.

Например, рассматривая ткани конечности, можно выделить кожные покровы, жировую и мышечную ткани, костную и сосудистую ткани, костный мозг и т. д.. В то же время, в кости мы различаем компактную и спонгиозную ткань, пронизывающие ткань макро- и микрососуды заполненные кровью, нервные стволы и т.д. Поэтому, говоря, к примеру, о проводимости костной ткани, мы понимаем, что это осредненный, интегральный показатель, вклад в который дают перечисленные выше составляющие.

В ряде практических задач нас интересует распределение полей и токов в макроскопически осредненных объемах биотканей. Каждую из тканей вполне можно рассматривать как однородную по своим физическим свойствам среду. Однако, часто возникает необходимость оценивать локальные параметры токов и полей, возникающих на границах раздела и в объемах микроскопических неоднородностей. Например, если необходимо рассчитать распределение индуцируемых токов в микрососудах, пронизывающих костную ткань при воздействии на конечность электромагнитных полей, то такую задачу целесообразно решать в несколько этапов.

На первом этапе рассматривают модель конечности, в которой присутствуют кожные покровы, мышечная и костная ткани, костномозговой канал. Задавшись геометрическими параметрами тканей и их проводимостями, рассчитывают распределение токов и полей в такой модели. На следующем этапе с учетом расположения сосудов относительно тела кости и внешнего поля рассматривают модель кровеносного сосуда, включающую внешнюю среду (тело кости), собственно стенку кровеносного сосуда и заполняющую его кровь. Полученные на первом этапе поля и токи будут внешними по отношению к кровеносному сосуду. Таким образом, расчет сведется к рассмотрению цилиндрического включения с заданной проводимостью стенок, заполненного проводящей средой (кровью), которое находится во внешнем поле с заданными характеристиками. Здесь мы не будем касаться допущений и погрешностей такого подхода. Отметим, что его реализация сводится к последовательному решению по сути однотипных задач. Для иллюстрации этого подхода рассмотрим типичную задачу, возникающую при таких расчетах.

Пусть имеется неограниченная среда с проводимостью , в которой находится достаточно протяженное цилиндрическое включение с внутренним радиусом _, внешним и проводимостью . Внутри цилиндра имеется среда с проводимостью . Кроме того, пусть при отсутствии включения в среде течёт однородный ток с плотностью , причем его направление перпендикулярно оси цилиндра (рис. 2.3). Необходимо найти распределение токов в такой системе.

Будем производить расчеты в центральной плоскости с тем, чтобы не учитывать эффекты конечной длины включения. В этом случае задача нахождения распределения электрического потенциала будет плоской и её решение является решением уравнения Лапласа для распределения электрического потенциала, которое в полярных координатах имеет вид

(2.21)

Общее решение уравнения Лапласа в полярных координатах определяется выражением

(2.22)

где константы определяются из граничных условий и особенностей рассматриваемой задачи.

Рис. 2.3. Цилиндрическое включение в поле постоянного тока.

В нашем случае, в силу симметрии задачи и, следовательно, в выражении (2.22) члены с отсутствуют. Рассмотрим сначала вид решения для внутренней области 2 .

Вследствие конечности потенциала при =0 из выражения (2.22) имеем

(2.23)

Учитывая, что решение (2.23) должно иметь период равный и принимая потенциал в центре равным нулю, получаем выражение для потенциала внутренней области в виде

(2.24)

Аналогичные рассуждения приводят к тому, что для областей 0 и 1 решения будут иметь следующий вид:

(2.25)

При большом удалении от цилиндрического включения поле практически однородное, следовательно должно выполняться условие

(2.26)

где - напряженность электрического поля в невозмущенной среде (на бесконечности).

Рис.2.4. Схематическое обозначение сечения тканей бедра.

Следовательно, имеем:

(2.27)

На границах раздела и выполняются условия непрерывности потенциала и нормальных составляющих плотности тока. Нормальные компоненты плотности тока, как известно, определяются выражениями:

,

(2.28)

Следовательно, имеем две системы уравнений для нахождения оставшихся коэффициентов.

(2.29)

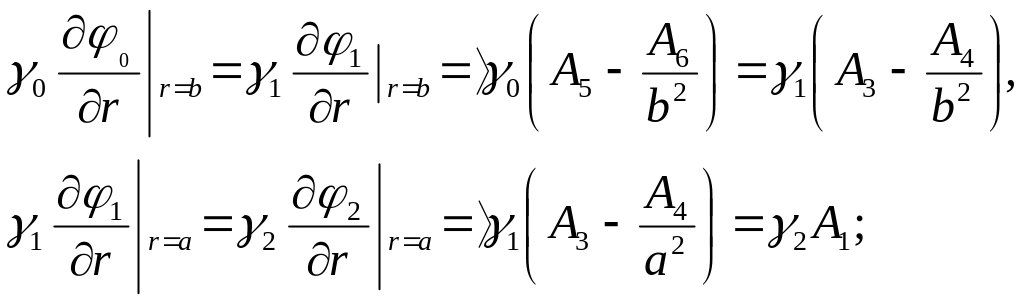(2.30)

здесь

Решая системы (2.29)…(2.30), получаем

(2.31)

Для нахождения радиальной, азимутальной компонент плотности тока и её модуля имеем соотношения:

(2.32)

В частности, для напряженности поля в толще стенок цилиндрического включения получаем

(2.33)

Приведённые соотношения позволяют численно оценивать локальные плотности токов во многих практических ситуациях.

Пример процедуры расчета параметров электрофизической стимуляции.

В качестве примера рассмотрим задачу оценки параметров бесконтактной электрической стимуляции кровеносных сосудов сегмента конечности (например, бедра) представленного на рис. 2.4.

Пусть в стенке бедренной артерии необходимо создать плотность тока с заданной амплитудой и законом изменения во времени j (t). Мы считаем, что функция j(t) нам известна и получена теоретическим, либо экспериментальным путем. Определение вида функции j (t) могло быть продиктовано различными практическими задачами, например сокращением гладкомышечной мускулатуры кровеносного сосуда, созданием в патологически пораженном сосуде токов, адекватных репаративным процессам, и т.п.

В рассматриваемом сегменте конечности имеются различные по физическим свойствам биоткани. В рассматриваемом сегменте будем учитывать наличие мягких тканей, кости с костным мозгом, кровеносный сосуд с кровью, а также расположение сосуда относительно кости и ориентацию вектора напряжённости внешнего электрического поля. Пусть, для простоты, внешнее воздействие оказывается однородным электрическим полем, изменяющимся во времени по закону Е(t). Такие поля можно создать с помощью конденсаторных пластин, между которыми располагается конечность, либо с помощью двух пар соленоидов со встречно- включенными магнитными полями.

Таким образом, задача состоит в нахождении параметров поля Е (t) которое создает в стенках рассматриваемого кровеносного сосуда ток с плотностью j (t) (см. рис. 2.4).

В соответствиии с материалом предыдущих разделов, на первом этапе решения задачи находится поверхностная плотность связанных зарядов на границе раздела конечность-воздух. Для нашей геометрии поля и конечности

(2.34)

Тогда плотность однородного тока в мягких тканях конечности непосредственно у поверхности кожи можно оценить как

(2.35)

На следующем этапе рассматриваем задачу о костной ткани, находящейся в поле однородного тока, и по формулам, приведенным в разделе 2.2, рассчитываем токи, текущие в мягких тканях непосредственно в области локализации кровеносного сосуда (эта область задается радиусом r и углом ).

Последний этап состоит в расчете токов, возникающих в стенке кровеносного сосуда, помещенного в поле однородного тока, плотность входного тока которого найдена на предыдущем этапе расчета. Приравнивая плотность этого тока к заданной функции j (t), в конечном итоге получаем функциональную связь в виде

, (2.36)

которая связывает геометрические параметры задачи, проводимости сред, заданный ток j (t) c напряженностью внешнего поля. Решая это уравнение, находим закон, по которому должно меняться поле Е (t).

Если поле Е (t) создается парой встречно-включенных соленоидов (рис. 2.5), то в соответствии с законом электромагнитной индукции для нахождения Е (t) имеем

(2.37)

где - ток в соленоидах; к - коэффициент, который учитывает их радиус и длину, L – индуктивность соленоида.

Тогда уравнение (2.36) приобретает вид

(2.38)

Для тока в соленоидах имеем выражение

(2.39)

Константы и целесообразно выбирать такими, чтобы ток в соленоидах в начале и конце импульса длительностью Т был равен нулю (импульс начинается и заканчивается при нулевом токе). Следовательно, окончательно получаем

(2.40)

Замечание. При выводе соотношений (2.37)…(2.40) нами принималось, что индуцируемое электрическое поле, создаваемое соленоидами, однородное. Количественной мерой справедливости такого допущения является степень неоднородности поля в области, занимаемой конечностью. Можно показать, что если радиус соленоидов и расстояние между ними d выбраны так, что , то неоднородность поля в пределах области пространства занятой конечностью не хуже 25%. Кроме того, в ходе расчетов мы принимали допущения, связанные с малостью характерных размеров сечения кровеносного сосуда по сравнению с сечением кости. Условия и степень справедливости этих допущений нами рассматривались в разделе 2.2