2.1.1. Переменное магнитное поле.

Пусть имеется сегмент тела или весь организм, помещенный в однородное по пространству и переменное по времени магнитное поле, вектор которого параллелен оси сегмента. Примем форму сегмента близкой цилиндрической (рис.2.1). В этом случае сегмент находится в поле с плотностью потока энергии, которая определяется вектором Пойнтинга.

Рис.2.1.

S =[E H], где H – напряженность магнитного поля, Е – напряженность индуцированного электрического поля. Величина последней находится с помощью теоремы о циркуляции, что для нашего случая даёт следующие соотношения:

(2.4)

S – здесь уже площадь контура

Электрическое поле создает в сегменте круговой ток с плотностью, которая определяется дифференциальным законом Ома:

j =  E =– gmm0wrH0 coswt/2

(2.5)

где  - проводимость среды.

Этот ток, в свою очередь, создает своё магнитное поле . Напряженность определяется как поле многослойного соленоида с внутренним радиусом, равным нулю, и внешним радиусом . Напряженность поля в точке А создаваемое элементарным соленоидом с внутренним радиусом r и внешним r+dr определяется формулой (рис. 2.1):

(2.6)

где I₁=jhdr – ток элементарного соленоида.

Суммируя магнитные поля от отдельных соленоидальных слоев при изменении радиуса от 0 до и учитывая (2.6), получим

	(2.7)

где - функция, зависящая от геометрических параметров. После чего нетрудно найти плотность потока мощности, которая оказывается пропорциональной и нелинейно распределяется по объёму сегмента.

2.1.2.Импульсные магнитные поля.

Если за время напряженность магнитного поля меняется на , то напряжённость вихревого электрического поля можно оценить как:

(2.8)

Аналогично предыдущим расчетам находится напряженность магнитного поля в теле и плотность потока энергии.

	(2.9)

2.1.3. Постоянное магнитное поле.

Если тело находится в постоянном во времени магнитном поле с напряженностью , которое неоднородно по пространству, то лишь при движении тела с некоторой скоростью V в нём возникает ЭДС индукции

Е_инд (рис. 2.2).

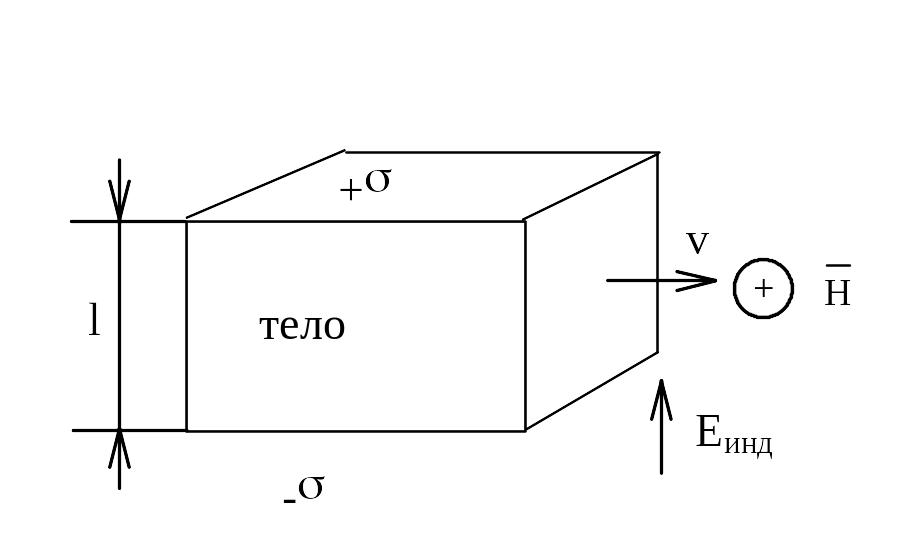
Рис. 2.2.

где l -размер тела; - угол между векторами и V.

Если магнитное поле однородно при постоянной скорости  , имеем Е_инд= const. Т.е. возникающее первоначально разделение зарядов в теле меняться не будет, следовательно, ток не течёт. При изменении скорости движения, либо при наличии пространственной неоднородности поля будет меняться Е_инд, а значит, изменяется поверхностная плотность компенсационного разряда _. В результате в теле течет ток с плотностью j.

Изменение поверхностной плотности заряда определяется как:

(2.10)

где – диэлектрическая проницаемость окружающей среды;

dE– изменение напряженности индуцируемого электрического поля. Поскольку

,

то

,

где

,

,

,

В результате получаем

(2.11)

Ток j создает магнитное поле напряженность которого определяется формулой:

(2.12)

Напряженность эквивалентного электрического поля (создающего такую же плотность тока) в теле находится на основе Закона Ома:

(2.13)

Плотность потока мощности, поглощаемого телом, составит в этом случае

(2.14)