П. 4. Параллельный lc-контур

Конденсаторы, которые используются в сочетании с индуктивностями, позволяют “заострять” частотную характеристику схемы, т.е. на некоторой частоте она имеет большой всплеск. Обычно параллельный LC-контур включают в схему так, как это показано на рис. П6.

а)

Рис. П6. Схема включения параллельного LC-контура (a), амплитудно-частотная (б) и фазо-частотная (в) характеристики

В точке 1 без учета резистора R получаем (L и C включены параллельно)

Отсюда резонансная частота находится из уравнения 1-ω²LC=0

Фазовая характеристика при ω<ω_рез имеет сдвиг π/2 (индуктивный характер), а при ω>ω_рез обладает фазовым сдвигом в -π/2 (емкостный характер). Коэффициент добротности Q позволяет оценить характеристику контура: чем больше Q, тем острее характеристика. Добротность равна резонансной частоте ω_рез, поделенной на ширину пика, определенную по точкам -3дб (см. фильтры ВЧ и НЧ).

П. 5. Последовательный lc-контур

Последовательный LC-контур изображен на рис. П.7.

а)

Рис. П7. Схема включения последовательного LC-контура (а), амплитудно-частотная (б) и фазо-частотная (в) характеристики

В точке 1 без учета резистора R получим (L и C включены последовательно)

или, заменив оператор p на jω, находим

О тсюда резонансная частота (Z→0) находится из уравнения ω²LC-1=0

Амлитудно-частотная и фазо-частотная характеристики приведены на рис. П7, б, в.

Такая схема на резонансной частоте или вблизи нее как бы “захватывает” сигнал и “заземляет” его (Z_рез=0). Фазовая характеристика при ω>ω_рез имеет сдвиг -π/2 (емкостный характер), а при ω<ω_рез обладает фазовым сдвигом в +π/2 (индуктивный характер).

П. 6. Кварцевая стабилизация импульсных генераторов

Кварц – двуокись кремния, горный хрусталь, песок и т.д. Некоторые разновидности кварца обладают пьезоэлектрическими свойствами. С недавних пор научились производить синтетические пьезоматериалы.

Кварц используется для термостабилизации потому, что обладает относительно хорошей термоустойчивостью и стабильностью, защищенностью по отношению к внешним воздействиям.

Пьезосвойства состоят в том, что если к пьезоматериалу прикладывать механические воздействия, то он генерирует напряжение, или, если прикладывать внешнее напряжение, то образуется механическое движение.

Если к кварцу подвести синусоидальное напряжение и менять частоту этого напряжения, то кварц на некоторых частотах образует электромеханический резонанс на 1, 2, 3, 4, … , 25 гармониках (см. рис. П8).

Рис. П8. Амплитуды резонанса

В автоматике и электронике под гармониками подразумевают продукт преобразования синусоиды нелинейностью, т.е. если есть “черный ящик”, на вход которого подается синусоида и на выходе тоже синусоида, то говорят, что нелинейных искажений нет. Если на выходе дополнительно к синусоиде образуются гармоники, то это результат нелинейных искажений.

По отношению к кварцу гармониками называют частоты, на которых он резонирует, т.е. гармоники не есть результат нелинейных искажений. Здесь другой смысл названия гармоники: частота, на которой возникают резонансные колебания.

Физический смысл гармоник.

После приложения синусоидального воздействия возникает электромеханическая волна. На некоторой частоте на толщине кварца укладываются ровно две полуволны (см. рис. П9), на других частотах не укладываются. Если две полуволны, то от основания или от верхней части кварца происходит отражение (отраженная волна – штриховая на рис. П9), образуется стоячая волна, как результат сложения прямой и обратной волн. Именно для этого случая образуется первая гармоника, электромеханический резонанс.

Только на частоте стоячей волны есть первая гармоника. При этом добротность примерно 25 000 единиц.

Рис. П9. Первая резонансная гармоника

Рис. П10. Возбуждающие и генерируемые колебания компенсируют друг друга

Физический смысл гармоник заключается в том, что это те частоты (1, 2, 3, … до 25 и более), на которых на толщине кварца укладывается целое количество периодов колебаний, т.е. образуются стоячие волны (рис. П11).

Рис. П11. Гармоники кварца

Таким образом, один и тот же кварц может вибрировать на любой гармонике рис. П11.

Резонанс возможен только на одной частоте, потому что при резонировании вершина и дно колеблются, следовательно, для других частот уже не будет устойчивого отражения из–за вибрации. Амплитуда вибрации убывает с возрастанием номера, потому что с одной стороны, более высокие частоты сильнее затухают в кристалле, с другой стороны, полировка сторон кварца на микроуровне имеет шероховатость и становится соизмеримой с более короткими длинами волн, хуже отражение.

Частоту вибрации первой гармоники можно рассчитать по следующей формуле

где h – высота между подводящими и отводящими электрический ток пластинами, [мм].

Если необходимо снизить частоту генерации, то делают камертонные кварцы (см. рис. П12).

Рис. П12. Камертонный кварц

В данной конструкции звуковые колебания распространяются вдоль камертонной формы, т.е. проходят большой путь, поэтому образуется длинная стоячая волна первой гармоники (частота f ≈ 30 кГц).

При анализе уже действующих электронных схем, или при их разработке, должны быть удовлетворены условия начала возбуждения. Т.е. внешняя электронная схема должна содержать резонансный контур, дополнительно к кварцу. За счет последнего будет выбираться гармоника кварца.

Необходимо, чтобы настройка этого резонансного контура, термонестабильного в своей сущности, не выходила за пределы резонансной частоты кварца.

В связи с тем, что кварц – это электромеханическое устройство, а процессы в нем имеют, прежде всего, механический характер, для изменения частоты настройки бесполезно ставить конденсаторы последовательно или параллельно кварцу. Тем не менее, в литературе в некоторых случаях утверждается, что это возможно. Там имеется в виду, что установочные конденсаторы изменяют частоту настройки возбуждающего генератора, но не кварца, а вместе с ней частично перестраивают и резонирующую частоту кварца в пределах первой или любой другой гармоники, но не более.

В литературе для объяснения свойств кварца используют резонансный LC контур (см. рис. П13).

Рис. П13. Резонансный LC-контур

Говорят, что процессы в контуре, изображенном на рис. П13, и в кварце подобны друг другу, но, тем не менее, физический смысл процессов совершенно разный. В этом контуре резонанс наблюдается только на двух частотах, а в кварце, по крайней мере, на двадцати пяти гармониках (или больше). Здесь наблюдаются последовательный и параллельный резонансы. В кварце возбуждаются колебания, совпадающие по фазе и противофазные,

генерируемые в процессе вибрации кристалла.

В кварце нет настоящих емкостей, индуктивности и резистивности. Под индуктивностью кварца понимают его массу, под емкостью С – его податливость, под резистивносттью – тепловые потери в процессе вибрации, а С₀ – емкость пластин, через которые подводится внешнее возбуждающее напряжение.

В контуре на рис. П13 выделим последовательную левую цепь и параллельно подключенный к ней конденсатор С₀. Для упрощения пренебрежем величиной сопротивления R. Тогда общее сопротивление в операторной форме будет равно

Из этого выражения следует, что есть две резонансные частоты (если перейти к частотной форме ω=2πf):

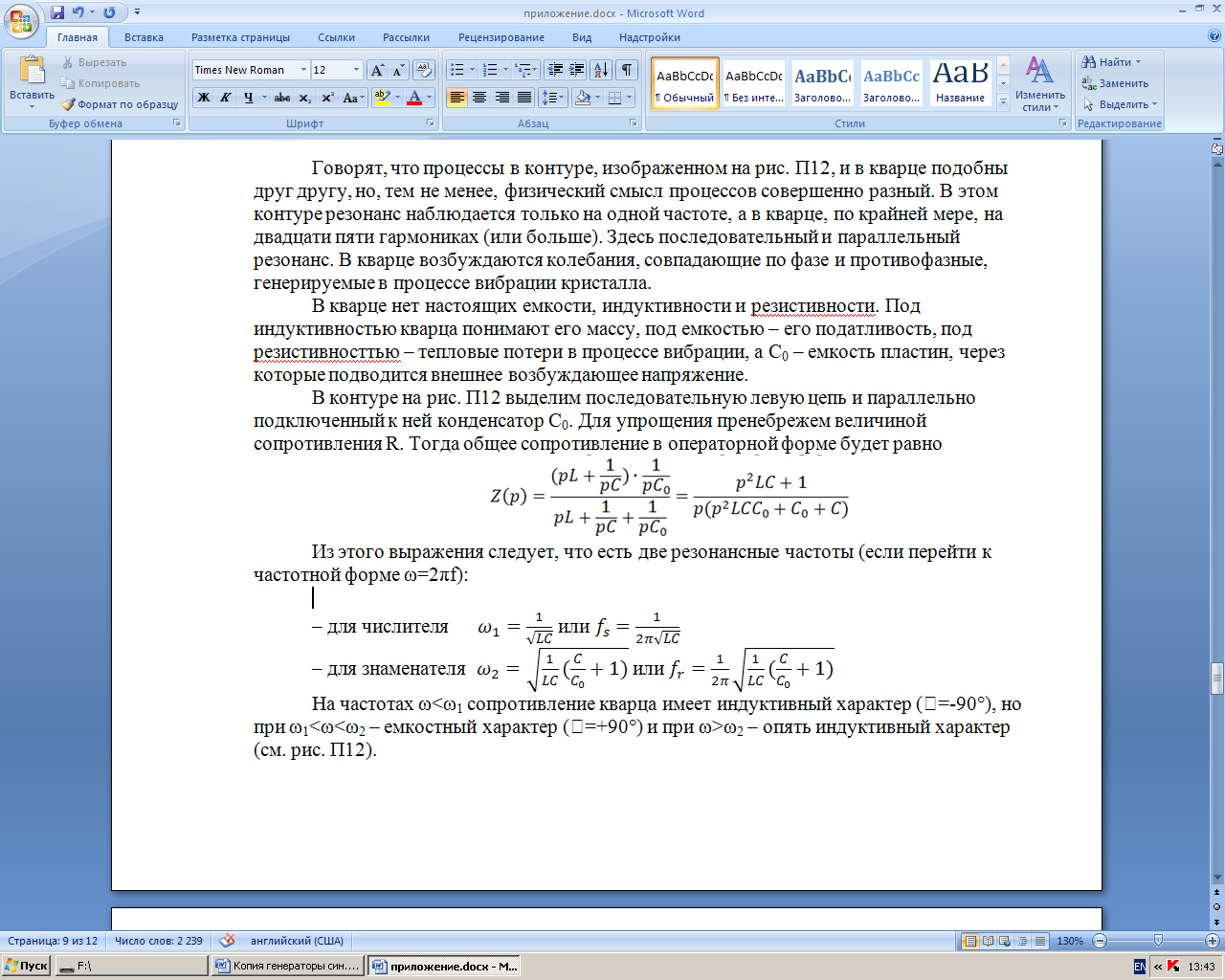
– для числителя

– для знаменателя

На частотах ω<ω₁ сопротивление кварца имеет емкостный характер (φ=-90°), но при ω₁<ω<ω₂ – индуктивный характер (φ=+90°) и при ω>ω₂ – опять емкостный характер (см. рис. П14).

Так как С₀ >> C, то частоты практически совпадают, тем более, что добротность кварца составляет примерно 25000, т.е. образуется очень узкая полоса пропускания. Таким образом, получена типовая формула резонансной частоты для LC контура. Но кварц – не LC контур, это вибрирующее на разных частотах (гармониках) устройство, не имеющее в своем составе индуктивностей, емкостей и т.д.

Отличие: в подобных формулах для аппроксимации кварца пишут цифры 1, 2, 3, …, 25, соответствующие номеру гармоники возбуждения.

Если сравнить с добротностью LC контура, то у него в лучшем случае добротность принимает значения до 500 – 600 единиц, т.е. кварц обладает чрезвычайно узкой резонансной характеристикой (см. рис. П14), причем выделяют в окрестности этого резонанса две частоты f_s и f_r, где

f_s – частота последовательного резонанса,

f_r – частота параллельного резонанса,

Q – добротность,

Δf отсчитывается на уровне 0,7 от максимума (-3дб).

0.707

Рис. П14. Амплитудно-частотная (а) и фазо-частотная (б) характеристики кварца