Преобразование восьмеричных чисел в двоичные и обратно

Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. Например:

Пусть требуется перевести восьмеричное число 24738 в двоичное число:

Поскольку . Следует помнить, что восьмеричное число кодируется тремя битами, и выписывать триады нужно полностью. Исключением из этого правила может служить только старшая триада, в которой старший бит (СБ) равен нулю.

Преобразование шестнадцатеричных чисел в двоичные и обратно

Алгоритм перевода чисел из шестнадцатеричной системы счисления двоичную крайне прост. Необходимо только заменить каждую цифру шестнадцатеричного числа ее эквивалентом в двоичной системе счисления (в случае положительных чисел). Каждое шестнадцатеричное число следует заменять двоичным, дополняя его до 4 разрядов (в сторону старших разрядов). Например:

Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Например:

38/39.Мультиплексоры и демультиплексоры

Мультиплексор – комбинационное логическое устройство, предназначенное для управляемой передачи данных от нескольких источников информации в один выходной канал.

Мультиплексор имеет 1 выход и 2 группы входов: адресные и информационные. Код, подаваемый на адресные входы, определяет, какой из информационных входов в данный момент времени подключен к выходу. Если число адресных входов равно N, то число информационных равно .

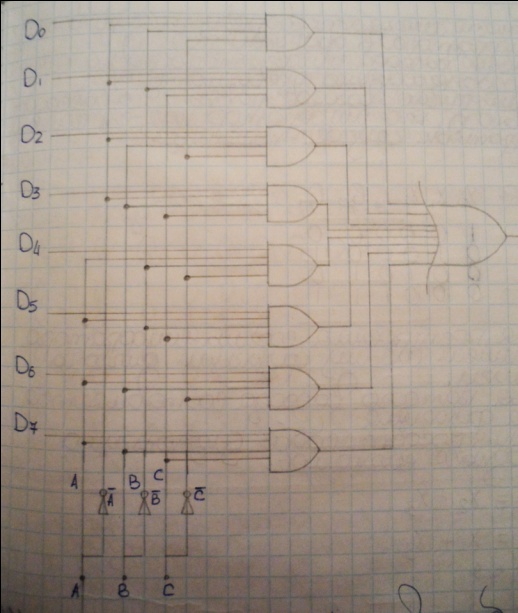
	B	C
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Демультиплексор - логическое устройство, предназначенное для управляемой передачи данных от одного источника информации в несколько выходных каналов. Демультиплексор имеет один информационный вход, N адресных входов и выходов.

0	0			0	0
0	1	0		0	0
1	0	0	0		0
1	1	0	0	0

12.Выполнение арифметических действий в позиционных системах счисления

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным вам правилам.

Сложение. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел:

Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания.

С ложение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов в старшие. В качестве примера сложим в столбик двоичные числа и :

Проверим правильность вычислений сложением в десятичной системе счисления. Переведем двоичные числа в десятичную систему счисления и затем их сложим:

Теперь переведем результат двоичного сложения в десятичное число:

Сравним результаты - сложение выполнено правильно.

Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой:

Вычитание многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей вычитания с учетом возможных заемов из старших разрядов. В качестве примера произведем вычитание двоичных чисел и :

У множение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел:

Умножение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на цифры множителя. В качестве примера произведем умножение двоичных чисел и :

Д еление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа и :

Арифметические операции в восьмеричной и шестнадцатеричной системах счисления. Аналогично можно выполнять арифметические действия в восьмеричной и шестнадцатеричной системах счисления. Необходимо только помнить, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления:

Для проведения арифметических операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему.