
- •Логика высказываний.
- •Логическая равносильность формул.
- •Нормальные формы формул алгебры высказываний.
- •Метод резолюций в алгебре высказываний
- •Алгебра логических значений
- •Булевы многочлены и булевы функции
- •Системы булевых функций
- •Переключательные схемы
- •Минимизация булевых многочленов
- •Логика предикатов Понятие предиката
- •Алгебра предикатов
- •Формулы алгебры предикатов
- •Если , – формулы, то формулами являются также выражения
- •Интерпретации формул алгебры предикатов
- •Тавтологии алгебры предикатов
- •Логическая равносильность формул алгебры предикатов
- •Логическое следование формул алгебры предикатов
- •Формальные исчисления
- •Исчисление высказываний
- •Исчисление предикатов
- •Аксиоматические теории первого порядка
- •Интерпретация теории первого порядка
- •Выполнимость формул теории первого порядка
- •Примеры теорий первого порядка
- •Свойства теорий первого порядка
- •Проблема общезначимости формул алгебры предикатов
- •Метод семантических таблиц
- •Автоматическое доказательство теорем
- •Нормальные формы для формул алгебры предикатов
- •Метод резолюций в исчислении предикатов
- •Элементы теории алгоритмов
- •Характерные особенности моделей вычислений Общие понятия алгоритма и вычислимой функции.
- •Формальные грамматики
- •Нормальные алгорифмы Маркова
- •Рекурсивные функции
- •Машины Тьюринга
- •Сложность вычислений
- •Сложность алгоритмов
- •Полиномиальные сведения
Формулы алгебры предикатов
Определение.
Алгеброй предикатов называется множество всех предикатов P с логическими операциями и операциями квантификации , для всех предметных переменных x.
Свойства алгебры предикатов P описываются с помощью специальных формул, которые строятся из символов предикатов и предметных переменных с помощью специальных вспомогательных символов – скобок и знаков логических операций над предикатами.
Алфавит алгебры предикатов состоит из следующих символов:
предметные переменные
 ,
которые используются для обозначения
элементов множества допустимых значений,
,
которые используются для обозначения
элементов множества допустимых значений,
n-местные предикатные символы , которые используются для обозначения n-местных предикатов на множестве допустимых значений,
символы логических операций
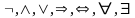 ,
,вспомогательные символы (,) и другие.
Формулы алгебры предикатов определяются по индукции следующим образом:
для любого n-местного предикатного символа и любых n предметных переменных выражение есть формула, которая называется элементарной формулой;
Если , – формулы, то формулами являются также выражения
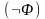 ,
,
,
,
;
,
,
,
,
;
если – формула и x – предметная переменная, то формулами являются также выражения
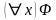 ,
,
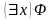 ;
при этом формула
называется областью
действия
соответствующего квантора.
;
при этом формула
называется областью
действия
соответствующего квантора.
Если
в формулу
входят переменные
,
то записывают
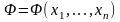 .
.
Вхождение
предметной переменной x
в
формулу
называется связным,
если она является переменной одного из
кванторов
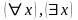 или находится в области действия одного
из этих кванторов;
в
противном случае вхождение предметной
переменной x
в
формулу
называется свободным.
или находится в области действия одного
из этих кванторов;
в
противном случае вхождение предметной
переменной x
в
формулу
называется свободным.
Формула без свободных вхождений переменных называется замкнутой формулой или предложением.
Интерпретации формул алгебры предикатов
Область интерпретации – непустое множество M, которое является областью возможных значений всех предметных переменных.
n-местным
предикатным символам
присваиваются конкретные значения
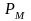 n-местных
предикатов на множестве M.
n-местных
предикатов на множестве M.
Соответствие
:
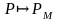 называется
интерпретацией
предикатных символов.
называется
интерпретацией
предикатных символов.
Область
интерпретации M
вместе с интерпретацией предикатных
символов
называется
интерпретацией
формул алгебры предикатов
и обозначается
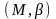 или просто M.
или просто M.
При наличии интерпретации M конкретные значения предметным переменным формул алгебры предикатов присваиваются с помощью отображения множества всех предметных переменных X в область интерпретации M.
Такие отображения называются оценками предметных переменных.
Выполнимость
формулы
в интерпретации M
при оценке
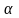 обозначается
обозначается
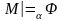 и определяется следующим образом:
и определяется следующим образом:
если
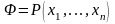 для n-местного
предикатного символа
и предметных переменных
,
то
тогда и только тогда, когда высказывание
для n-местного
предикатного символа
и предметных переменных
,
то
тогда и только тогда, когда высказывание
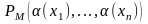 истинно;
истинно;если
 для формулы ,
то
тогда и только тогда, когда неверно,
что
для формулы ,
то
тогда и только тогда, когда неверно,
что
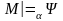 ;
;если
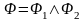 для формул
для формул
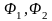 ,
то
тогда и только тогда, когда
,
то
тогда и только тогда, когда
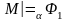 и
и
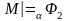 ;
;если
 для формул
,
то
тогда и только тогда, когда
или
;
для формул
,
то
тогда и только тогда, когда
или
;если
 для формул
,
то
тогда и только тогда, когда неверно,
что
и
для формул
,
то
тогда и только тогда, когда неверно,
что
и
 ;
;если
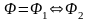 для формул
,
то
тогда и только тогда, когда
,
одновременно верны или нет;
для формул
,
то
тогда и только тогда, когда
,
одновременно верны или нет;если
 для некоторой формулы ,
то
тогда и только тогда, когда
для некоторой формулы ,
то
тогда и только тогда, когда
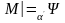 для всех оценок
для всех оценок
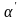 ,
отличающихся от оценки
возможно только на элементе x;
,
отличающихся от оценки
возможно только на элементе x;если
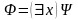 для некоторой формулы ,
то
тогда и только тогда, когда
для некоторой оценки
,
отличающейся от оценки
возможно только на элементе x.
для некоторой формулы ,
то
тогда и только тогда, когда
для некоторой оценки
,
отличающейся от оценки
возможно только на элементе x.
Определение. В интерпретации M формула называется:
общезначимой (или тождественно истинной), если при любых оценках ;
выполнимой, если для некоторой оценки ;
опровержимой, если для некоторой оценки неверно, что ;
тождественно ложной, если для любой оценки неверно, что .
Формула
общезначима в интерпретации M,
если при подстановке в нее вместо n-арных
предикатных символов
их интерпретаций
она превращается в тождественно истинный
на множестве M
предикат. Символическая запись
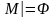 .
.
Формула в интерпретации M выполнима, опровержима или тождественно ложна, если при подстановке в нее вместо n-арных предикатных символов их интерпретаций она превращается соответственно в выполнимый, опровержимый или тождественно ложный на множестве M предикат .
