
- •Логика высказываний.
- •Логическая равносильность формул.
- •Нормальные формы формул алгебры высказываний.
- •Метод резолюций в алгебре высказываний
- •Алгебра логических значений
- •Булевы многочлены и булевы функции
- •Системы булевых функций
- •Переключательные схемы
- •Минимизация булевых многочленов
- •Логика предикатов Понятие предиката
- •Алгебра предикатов
- •Формулы алгебры предикатов
- •Если , – формулы, то формулами являются также выражения
- •Интерпретации формул алгебры предикатов
- •Тавтологии алгебры предикатов
- •Логическая равносильность формул алгебры предикатов
- •Логическое следование формул алгебры предикатов
- •Формальные исчисления
- •Исчисление высказываний
- •Исчисление предикатов
- •Аксиоматические теории первого порядка
- •Интерпретация теории первого порядка
- •Выполнимость формул теории первого порядка
- •Примеры теорий первого порядка
- •Свойства теорий первого порядка
- •Проблема общезначимости формул алгебры предикатов
- •Метод семантических таблиц
- •Автоматическое доказательство теорем
- •Нормальные формы для формул алгебры предикатов
- •Метод резолюций в исчислении предикатов
- •Элементы теории алгоритмов
- •Характерные особенности моделей вычислений Общие понятия алгоритма и вычислимой функции.
- •Формальные грамматики
- •Нормальные алгорифмы Маркова
- •Рекурсивные функции
- •Машины Тьюринга
- •Сложность вычислений
- •Сложность алгоритмов
- •Полиномиальные сведения
Метод резолюций в алгебре высказываний
Определение.
Пусть для некоторой переменной X
дизъюнкты
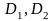 представимы в виде
представимы в виде
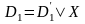 ,
,
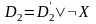 .
Тогда дизъюнкт
.
Тогда дизъюнкт
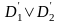 называется резольвентой
дизъюнктов
по переменной X
и обозначается
ResX
называется резольвентой
дизъюнктов
по переменной X
и обозначается
ResX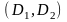 .
.
Резольвента
дизъюнктов
по некоторой переменной X
называется
резольвентой
дизъюнктов
и обозначается Res
.
По определению
Res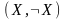 =0.
=0.
Определение.
Резолютивным
выводом формулы
из множества дизъюнктов
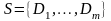 называется
такая
последовательность формул
называется
такая
последовательность формул
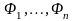 ,
что:
,
что:
n=;
каждая из формул i (i=1,…,n) либо принадлежит множеству S, либо является резольвентой
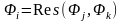 предыдущих формул j,
k
при некоторых 1j,ki.
предыдущих формул j,
k
при некоторых 1j,ki.
Теорема. Множество дизъюнктов противоречиво в том и только том случае, если существует резолютивный вывод значения 0 из множества S.
Так как по критерию логического следования соотношение
|=
равносильно условию
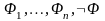 |=,
|=,
то справедлив следующий результат.
Следствие (Проверка логического следования формул).
Пусть для формул
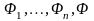 формула
формула
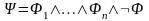 имеет КНФ
имеет КНФ
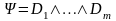 .
.
Тогда логическое следование |= равносильно существованию резолютивного вывода значения 0 из множества дизъюнктов .
Алгебра логических значений
Определение. Алгеброй называется непустое множество A с фиксированным набором операций f1,f2,…,fk, имеющих соответствующие определенные арности n1,n2,…,nk. При этом множество A называется базисным множеством алгебры и набор символов операций ={f1,f2,…,fk} соответствующей арности n1,n2,…,nk называется алгебраическим типом (или сигнатурой) алгебры.
Такая алгебра сокращенно обозначается (A;f1,f2,…,fk ), или (A;), или просто буквой A и называется алгеброй типа , или сокращенно -алгеброй.
Пример алгебры
дает множество {0,1} истинностных значений
высказываний с n-арными
операциями
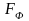 ,
которые являются функциями истинностных
значений формул логики высказываний
,
которые являются функциями истинностных
значений формул логики высказываний
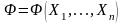 ,
образованных с помощью n
пропозициональных переменных
.
,
образованных с помощью n
пропозициональных переменных
.
Формула
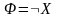 определяет унарную операцию
определяет унарную операцию
 ,
которая обозначается символом
,
которая обозначается символом
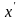 и называется отрицанием
или дополнением
переменной
и называется отрицанием
или дополнением
переменной
 .
.
Формулы
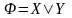 ,
,
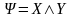 определяют бинарные операции
определяют бинарные операции
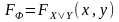 ,
,
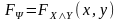 ,
которые обозначаются соответственно
символами
,
которые обозначаются соответственно
символами
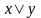 ,
,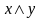 и называются дизъюнкцией
и конъюнкцией
переменных
,y.
и называются дизъюнкцией
и конъюнкцией
переменных
,y.
Операция
иногда называется также объединением
или суммой
переменных
,y
и обозначается соответственно через
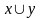 или
или
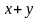 .
.
Операция
иногда называется также пересечением
или произведением
переменных
,y
и обозначается соответственно через
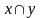 или
или
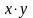 .
.
Алгебра B=({0,1},,,) впервые была введена в 19-ом веке английским математиком Дж.Булем с целью применения в логике математических методов.
Поэтому эта алгебра называется алгеброй Буля или алгеброй логических значений.
Теорема. Алгебра Буля B=({0,1},,,) удовлетворяет свойствам:
 ,
,
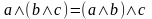 – ассоциативность дизъюнкции и
конъюнкции;
– ассоциативность дизъюнкции и
конъюнкции;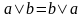 ,
,
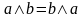 – коммутативность дизъюнкции и
конъюнкции;
– коммутативность дизъюнкции и
конъюнкции;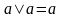 ,
,
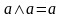 – идемпотентность дизъюнкции и
конъюнкции;
– идемпотентность дизъюнкции и
конъюнкции;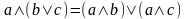 ,
,
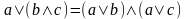 – дистрибутивность соответственно
конъюнкции относительно дизъюнкции и
дизъюнкции относительно конъюнкции;
– дистрибутивность соответственно
конъюнкции относительно дизъюнкции и
дизъюнкции относительно конъюнкции;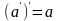 – идемпотентность
дополнения;
– идемпотентность
дополнения;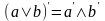 ,
,
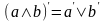 – законы де Моргана;
– законы де Моргана; ,
,
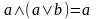 – законы поглощения;
– законы поглощения;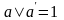 ,
,
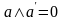 –
характеристическое свойство дополнения,
–
характеристическое свойство дополнения,
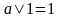 ,
,
 –
характеристическое свойство наибольшего
элемента 1,
–
характеристическое свойство наибольшего
элемента 1,
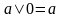 ,
,
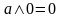 –
характеристическое свойство наименьшего
элемента 0.
–
характеристическое свойство наименьшего
элемента 0.
