
- •Логика высказываний.
- •Логическая равносильность формул.
- •Нормальные формы формул алгебры высказываний.
- •Метод резолюций в алгебре высказываний
- •Алгебра логических значений
- •Булевы многочлены и булевы функции
- •Системы булевых функций
- •Переключательные схемы
- •Минимизация булевых многочленов
- •Логика предикатов Понятие предиката
- •Алгебра предикатов
- •Формулы алгебры предикатов
- •Если , – формулы, то формулами являются также выражения
- •Интерпретации формул алгебры предикатов
- •Тавтологии алгебры предикатов
- •Логическая равносильность формул алгебры предикатов
- •Логическое следование формул алгебры предикатов
- •Формальные исчисления
- •Исчисление высказываний
- •Исчисление предикатов
- •Аксиоматические теории первого порядка
- •Интерпретация теории первого порядка
- •Выполнимость формул теории первого порядка
- •Примеры теорий первого порядка
- •Свойства теорий первого порядка
- •Проблема общезначимости формул алгебры предикатов
- •Метод семантических таблиц
- •Автоматическое доказательство теорем
- •Нормальные формы для формул алгебры предикатов
- •Метод резолюций в исчислении предикатов
- •Элементы теории алгоритмов
- •Характерные особенности моделей вычислений Общие понятия алгоритма и вычислимой функции.
- •Формальные грамматики
- •Нормальные алгорифмы Маркова
- •Рекурсивные функции
- •Машины Тьюринга
- •Сложность вычислений
- •Сложность алгоритмов
- •Полиномиальные сведения
Машины Тьюринга
Пост и Тьюринг исходили из того, что все действия, которые может производить любой алгоритм, можно разложить на некоторые канонические элементарные шаги, выполняемые подходяще устроенными вычислительными машинами.
Такие машины строго математически определяются следующим образом.
Определение. Машина Тьюринга Т - система, работающая в дискретные моменты времени t=0,1,2,... и состоящая из следующих частей:
1. Конечная
лента, разбитая
на конечное число ячеек,
- внешня
память машины. В
каждый момент времени t
в ячейках записаны буквы из алфавита
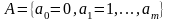 - внешний
алфавит машины.
Ячейки, в
которых записан символ 0, называются
пустыми. В
процессе работы машины: (1) ячейки ленты
могут менять свои состояния путем замены
записанных в них букв алфавита A
на
его другие буквы и (2) к существующим
ячейкам ленты может пристраиваться
неограниченное число дополнительных
ячеек, которые изначально считаются
пустыми.
- внешний
алфавит машины.
Ячейки, в
которых записан символ 0, называются
пустыми. В
процессе работы машины: (1) ячейки ленты
могут менять свои состояния путем замены
записанных в них букв алфавита A
на
его другие буквы и (2) к существующим
ячейкам ленты может пристраиваться
неограниченное число дополнительных
ячеек, которые изначально считаются
пустыми.
Лента считается
направленной и ее ячейки просматриваются
слева направо. Таким образом, если в
какой-то момент времени лента имеет r
ячеек, то
состояние
ленты полностью
описывается словом
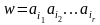 ,
где
,
где
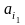 –
состояние первой (слева) ячейки,
–
состояние первой (слева) ячейки,
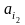 –
состояние
второй ячейки и т.д.
–
состояние
второй ячейки и т.д.
2.
Управляющая головка -
устройство, которое может перемещаться
вдоль ленты так, что в каждый рассматриваемый
момент времени t
оно находится напротив определенной
ячейки и имеет некоторое состояние qj
из конечного
множества
внутренних состояний машины
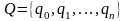 ,
Q∩А
= .
Состояние q0
называется
заключительным
и означает
завершение работы машины, а состояние
q1
называется
начальным и
означает начало работы машины. Если
головка в состоянии qj
находится напротив ячейки в состоянии
ai,
то говорят,
что машина просматривает эту ячейку
или наблюдает ее состояние qj.
,
Q∩А
= .
Состояние q0
называется
заключительным
и означает
завершение работы машины, а состояние
q1
называется
начальным и
означает начало работы машины. Если
головка в состоянии qj
находится напротив ячейки в состоянии
ai,
то говорят,
что машина просматривает эту ячейку
или наблюдает ее состояние qj.
В процессе работы машины управляющая головка: (1) может смещаться для просмотра соседних ячеек и (2) менять свои состояния путем замены записанных в ней букв алфавита Q на его другие буквы.
3.
Список команд или программа ,
представляющая собой последовательность
выражений T(i,j)
(где
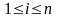 ,
,
 )
вида:
)
вида:
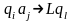 – означает
сдвиг
управляющей
головки, находящейся в состоянии qi
напротив
ячейки с буквой
aj,
на одну ячейку влево
с заменой
состояния управляющей головки qi
на состояние
ql;
– означает
сдвиг
управляющей
головки, находящейся в состоянии qi
напротив
ячейки с буквой
aj,
на одну ячейку влево
с заменой
состояния управляющей головки qi
на состояние
ql;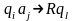 – означает
сдвиг
управляющей головки, находящейся в
состоянии qi
напротив
ячейки с буквой
aj,
на одну ячейку вправо
с заменой
состояния управляющей головки qi
на состояние
ql;
– означает
сдвиг
управляющей головки, находящейся в
состоянии qi
напротив
ячейки с буквой
aj,
на одну ячейку вправо
с заменой
состояния управляющей головки qi
на состояние
ql; – означает
замену
буквы aj
в ячейке,
напротив которой находится управляющая
головка
в состоянии qi,
на букву ak
с одновременной
заменой состояния управляющей головки
qi
на состояние
ql
.
– означает
замену
буквы aj
в ячейке,
напротив которой находится управляющая
головка
в состоянии qi,
на букву ak
с одновременной
заменой состояния управляющей головки
qi
на состояние
ql
.
Выражения T(i,j) называются командами.
При этом
предполагается, что
команды не могут начинаться со слов
q0aj,
содержащих символ заключительного
состояния
q0,
и что символы
L,R
не принадлежат
множеству
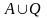 .
.
Машина Тьюринга Т - упорядоченная пятерка объектов Т=(A,Q,,q0,q1).
Работа машины Т происходит под действием команд из множества и заключается в изменении ее конфигураций, описывающих состояния ленты и управляющей головки, а также положение управляющей головки.
Если
лента находится в состоянии, которое
описывается словом
 над алфавитом
A,
и управляющая головка в состоянии
qi
просматривает на ленте j-ую
ячейку с состоянием aj,
то
соответствующая конфигурация K
машины Т
описывается выражением
над алфавитом
A,
и управляющая головка в состоянии
qi
просматривает на ленте j-ую
ячейку с состоянием aj,
то
соответствующая конфигурация K
машины Т
описывается выражением
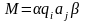 ,
которое называется
машинным словом.
,
которое называется
машинным словом.
Описывающие
конфигурации K
машинные
слова являются словами над алфавитом
,
содержащие единственный символ алфавита
,
правее
которого в слове непременно есть символ
алфавита
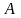 .
.
К называется начальной конфигурацией, если описывающее ее машинное слово содержит символ начального состояния q1, и заключительной конфигурацией, если ее машинное слово содержит символ заключительного состояния q0.
Изменение конфигураций К0,К1,К2,… машины Т под действием команд из множества происходит в дискретные моменты времени t = 0,1,2,... и описывается преобразованием соответствующих машинных слов M0,M1,M2,…по следующему правилу.
За один шаг работы машины Т ее машинное слово под действием команды T(i,j) преобразуется в новое машинное слово М' по формулам:
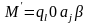 ,
если
,
если
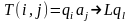 и α=,
и α=,
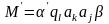 ,
если
и
,
если
и
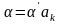 ,
,
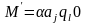 ,
если
,
если
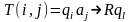 и β=,
и β=,
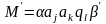 ,
если
и
,
если
и
 ,
,
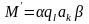 ,
если
,
если
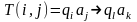 .
.
Символически такое
одношаговое преобразование машинных
слов обозначается
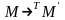 .
.
Если существует
такая последовательность преобразований
машинных слов
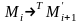 (где
(где
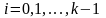 ),
для которой
),
для которой
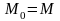 и
и
 ,
то пишут
,
то пишут
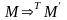 и говорят, что машинное
слово М' получается из машинного слова
М с помощью машины Т .
и говорят, что машинное
слово М' получается из машинного слова
М с помощью машины Т .
Если при этом во
всех преобразованиях
не достраиваются ячейки слева
(соответственно,
не достраиваются
ячейки ни слева, ни справа),
то пишут также
 (соответственно,
(соответственно,
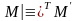 ).
).
Для машинного
слова М
обозначим
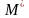 слово в редуцированном
алфавите
слово в редуцированном
алфавите
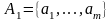 ,
которое получается из М
вычеркиванием
единственного вхождения буквы алфавита
и всех вхождений пустого символа a0=0.
,
которое получается из М
вычеркиванием
единственного вхождения буквы алфавита
и всех вхождений пустого символа a0=0.
Слово
алфавита
перерабатывается
машиной Т
в слово
редуцированного
алфавита
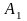 ,
если существует такая последовательность
преобразований машинных слов
,
если существует такая последовательность
преобразований машинных слов
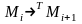 (где
),
для которой
(где
),
для которой
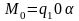 ,
,
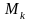 - машинное слово заключительной
конфигурации
и
- машинное слово заключительной
конфигурации
и
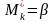 .
.
В этом случае будем
говорить, что машина
Т применима
к слову
,
и результат
переработки машиной
Т такого
слова
будем
обозначать
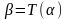 .
.
Если же машина Т слово не переводит в слово заключительной конфигурации, то будем говорить, что машина Т неприменима к слову .
Пример.
Пусть машина
Тьюринга
S
имеет внешний
алфавит
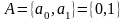 ,
внутренний алфавит
,
внутренний алфавит
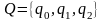 и программу :
и программу :
q10 → Rq2, q20 → q01, q11 → Rq1, q21 → Rq2.
Тогда
редуцированный
алфавит имеет
вид:
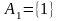 и слово
=11
машиной S
перерабатывается
в слово
=111,
так как
и слово
=11
машиной S
перерабатывается
в слово
=111,
так как
 и
и
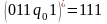 .
.
Машина S к любому слову над алфавитом приписывает справа символ 1.
Таким образом,
машина Тьюринга Т
определяет частичную
функцию f
из
в
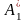 ,
область определения которой
,
область определения которой
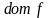 состоит из всех слов
алфавита
,
к которым применима машина Т,
и значения
которой для слов
состоит из всех слов
алфавита
,
к которым применима машина Т,
и значения
которой для слов
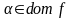 определяются по формуле:
определяются по формуле:
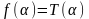 .
.
Определение.
Частичная
словарная функция f
из
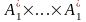 в
,
зависящая от n
переменных,
называется вычислимой
по Тьюрингу,
если существует машина Тьюринга Т
с внешним алфавитом
,
для которой при любых
в
,
зависящая от n
переменных,
называется вычислимой
по Тьюрингу,
если существует машина Тьюринга Т
с внешним алфавитом
,
для которой при любых
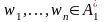 условие
условие
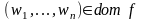 равносильно тому, что машина
Т применима
к слову
равносильно тому, что машина
Т применима
к слову
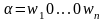 и результат
и результат
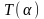 переработки машиной
Т такого
слова равен
значению функции
переработки машиной
Т такого
слова равен
значению функции
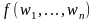 .
.
Теорема. Частичная словарная функция в том и только том случае будет вычислимой по Тьюрингу, если она является частично рекурсивной функцией.
Следствие.
Язык
в том и только том случае будет рекурсивным
(соответственно, рекурсивно
перечислимым), если его характеристическая
функция
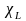 вычислима по Тьюрингу (соответственно,
язык L
является
множеством значений вычислимой
по Тьюрингу функции).
вычислима по Тьюрингу (соответственно,
язык L
является
множеством значений вычислимой
по Тьюрингу функции).
