Нормальные алгорифмы Маркова

Пусть А – произвольное непустое конечное множество, называемое алфавитом, и - два символа, не входящие в алфавит А. Множество A^* является множеством D_A возможных исходных данных нормального алгорифма Маркова A.

Определение. Нормальным алгорифмом Маркова (или просто алгорифмом) в алфавите А называется конечный линейно упорядоченный список A формул подстановок слов следующих двух типов:

(i) , (ii) , где .

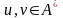Область применения алгоритма A:

1) если левая часть u хотя бы одной формулы из A является подсловом слова w, то выбираем первую такую формулу  в списке A и заменяем первое вхождение слова u в слово w на слово v, стоящее в правой части формулы , и ставим точку перед полученным словом 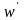, если формула  содержит точку, т.е. является формулой типа (ii) . Если при этом  - типа (i), то пишем w  и говорим, что A просто переводит w в , а если  - типа (ii), то пишем w  и говорим, что A заключительно переводит w в ;

2. если же никакая левая часть формул из A не является подсловом слова w, то слово не поддается алгорифму A;

Будем писать A(w)= в том и только том случае, если существует такая конечная последовательность слов 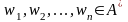, что

(1) ,

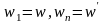(2) алгорифм A просто переводит w_i в w_i+1 для всех 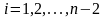и

(3) w_n-1  w_n.

Алгорифм A в алфавите 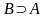называется алгорифмом над A.

Определение. Частичная словарная функция 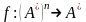над алфавитом называется нормально вычислимой, если существует такой алгорифм A над алфавитом 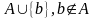, что A(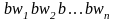 )=w тогда и только тогда, когда значение функции 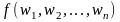определено и выполняется равенство .

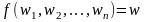Понятие нормально вычислимой словарной функции удовлетворяет всем свойствам вычислимых функций, т.е. является адекватной моделью вычислений.

Рекурсивные функции

Пусть 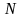– множество неотрицательных целых чисел и F – множество всех частичных функций нескольких числовых переменных из со значениями в .

0-функция, функция следования, n–местная функция проекции на m–ую координату и определяются по формулам:

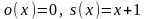и

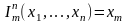
для любых значений .

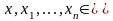Функции 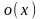, , 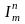называются также простейши­ми примитивно рекурсивными функциями.

На множестве F всех частичных функций нескольких числовых переменных рассмотрим следующих два оператора:

• оператор суперпозиции S ставит в соответствие каждой функции m переменных fF и m функциям n переме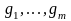нных F функцию n переменных , определяемую равенством:

;

• оператор примитивной рекурсии R ставит в соответствие каждой функции п+2 переменных fF и функции n переменных gF функцию n+1 переменных 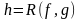, удовлетворяющую следующей схеме примитивной рекурсии:

,

.

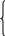
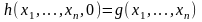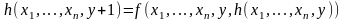В частности, при п = 0 схема примитивной рекурсии имеет следующий вид:

,

,

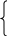
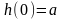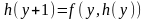где а — постоянная одноместная функция, равная числу а.

Определение.

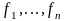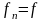Функция fF называется примитивно рекурсивной (сокращенно ПРФ), если суще­ствует последовательность функций F, в которой и всякая функция 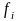является простейшей ПРФ или получается из предыдущих функций с помощью оператора суперпозиции S или оператора примитивной рекурсии R.

Примеры.

1. Функция сложения х+у примитивно рекурсивна в силу схемы примитивной рекурсии:

,

.

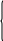
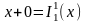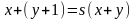2. Функция умножения примитивно рекурсивна в силу схемы примитивной рекурсии:

,

.

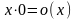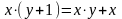Определение. n-арное отношение 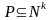называется примитивно рекурсивным (сокращенно ПРО), если примитивно рекурсивна его характеристическая функция

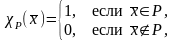
где - произвольный элемент множества .

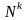Примеры. Отношения равенства х = у и делимости х|у примитивно рекурсивны, т.к. функци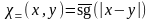и и 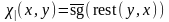примитивно рекурсивны.

Теорема 1.

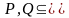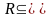
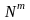Если отношения и примитивно рекурсивны, то отношения

, , ,

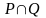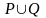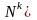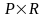
также примитивно рекурсивны.

Теорема 2.

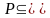
Если отношение 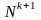примитивно рекурсивно, то примитивно рекурсивными являются также отношения

, .

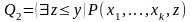Примеры.

1. Так как 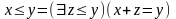, то отношение примитивно рекурсивно.

2. Так как 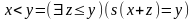, то отношение примитивно рекурсивно.

3. Множество всех простых чисел совпадает с примитивно рекурсивным унарным отношением

.

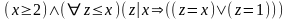На множестве F всех частичных функций нескольких числовых переменных рассмотрим еще один оператор , который называется оператором ограниченной минимизации:

каждой функции m переменных gF оператор  ставит в соответствие функцию m переменных f=(g), определяемую равенством:

,

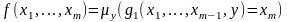где правая часть равенства обозначает наименьшее решение уравнения 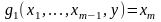относительно y.

Определение. Функция fF называется частично рекурсивной (сокращенно ЧРФ), если существует последовательность функций F, в которой и всякая функция является простейшей ПРФ или получается из предыдущих функций с помощью оператора суперпозиции S, оператора примитивной рекурсии R или оператора ограниченной минимизации .

При этом частично рекурсивная функция называется рекурсивной (сокращенно РФ), если она всюду определена, и общерекурсивной, если в определяющей ее последовательности F все функции являются всюду определенными.

Множества всех рекурсивных, общерекурсивных, частично рекурсивных и примитивно рекурсивных функций из множества F обозначим соответственно F_РФ, F_ЧРФ, F_ОРФ и F_ПРФ .

Из определений следуют включения множеств:

F_ПРФ  F_ОРФ  F_РФ  F_ЧРФ .

Известно, что F_ОРФ = F_РФ,

но все остальные включения являются собственными, т.е. F_ПРФ  F_ОРФ , F_РФ  F_ЧРФ .

Определение. Подмножество A множества называется рекурсивным (или разрешимым), если его характеристическая функция частично рекурсивна.

Определение. Подмножество A множества называется рекурсивно перечислимым, если A является множеством значений некоторой частично рекурсивной функции.

Конечные пересечения и конечные объединения рекурсивно перечислимых множеств являются рекурсивно перечислимыми множествами, а дополнения рекурсивно перечислимых множеств в общем случае не будут рекурсивно перечислимыми.

Теорема об универсальной функции.

Пусть F₁ - множество всех частично рекурсивных функций f из N в N. Тогда найдется такая вычислимая функция G из NN в N, что для любой функции 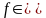F₁ найдется такое nN, что f совпадает с частично рекурсивной функцией 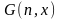из N в N.

При этом уравнение определяет вычислимую функцию из N в N определяет частично рекурсивную функцию f из N в N, которая не имеет всюду определенного рекурсивного продолжения на все множество N.

Следствие. Существует рекурсивно перечислимое нерекурсивное множество.

Понятия рекурсивной функции и частично рекурсивной функции, а также рекурсивного множества и рекурсивно перечислимого множества естественно переносятся на словарные функции и языки над любым конечным алфавитом с помощью биекции  множества A^* на множество N, которая определяется по правилам:

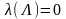и

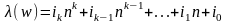
для непустого слова .

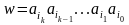Такая биекция  называется лексикографической функцией для алфавита A.

Лексикографическая функция  естественно продолжается на множество всех частичных словарных функций по правилу:

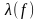есть числовая функция из 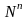со значениями в , которая определяется уравнением

для значений .

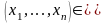Определение.

Частичная словарная функция называется частично рекурсивной (соответственно, рекурсивной или примитивно рекурсивной), если числовая функция частично рекурсивна (соответственно, рекурсивна или примитивно рекурсивна).

Определение.

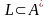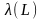Язык называется рекурсивным (соответственно, рекурсивно перечислимым), если числовое множество рекурсивно (соответственно, рекурсивно перечислимо).