- •Логика высказываний.
- •Логическая равносильность формул.
- •Нормальные формы формул алгебры высказываний.
- •Метод резолюций в алгебре высказываний
- •Алгебра логических значений
- •Булевы многочлены и булевы функции
- •Системы булевых функций
- •Переключательные схемы
- •Минимизация булевых многочленов
- •Логика предикатов Понятие предиката
- •Алгебра предикатов
- •Формулы алгебры предикатов
- •Если , – формулы, то формулами являются также выражения
- •Интерпретации формул алгебры предикатов
- •Тавтологии алгебры предикатов
- •Логическая равносильность формул алгебры предикатов
- •Логическое следование формул алгебры предикатов
- •Формальные исчисления
- •Исчисление высказываний
- •Исчисление предикатов
- •Аксиоматические теории первого порядка
- •Интерпретация теории первого порядка
- •Выполнимость формул теории первого порядка
- •Примеры теорий первого порядка
- •Свойства теорий первого порядка
- •Проблема общезначимости формул алгебры предикатов
- •Метод семантических таблиц
- •Автоматическое доказательство теорем
- •Нормальные формы для формул алгебры предикатов
- •Метод резолюций в исчислении предикатов
- •Элементы теории алгоритмов
- •Характерные особенности моделей вычислений Общие понятия алгоритма и вычислимой функции.
- •Формальные грамматики
- •Нормальные алгорифмы Маркова
- •Рекурсивные функции
- •Машины Тьюринга
- •Сложность вычислений
- •Сложность алгоритмов
- •Полиномиальные сведения
Формальные грамматики
Определение.
Грамматикой
называется
алгебраическая система
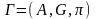 ,
состоящая из непустых
конечных множеств
А,G
и
конечного
бинарного отношения
между словами из множества
G+
и словами из множества (AG)*
.
Множество
А
называется
алфавитом
грамматики
и
множество
V=AG
–
полным
словарем
грамматики.
Элементы множества
G
не
принадлежат
алфавиту
А
и называются
грамматическими (или
металингвистическими)
символами
грамматики.
Элементы
(u,v)
отношения
называются правилами
грамматики
и символически обозначаются uv
. В
этом случае говорят, что слово v
получается
из слова u
по
правилу .
,
состоящая из непустых
конечных множеств
А,G
и
конечного
бинарного отношения
между словами из множества
G+
и словами из множества (AG)*
.
Множество
А
называется
алфавитом
грамматики
и
множество
V=AG
–
полным
словарем
грамматики.
Элементы множества
G
не
принадлежат
алфавиту
А
и называются
грамматическими (или
металингвистическими)
символами
грамматики.
Элементы
(u,v)
отношения
называются правилами
грамматики
и символически обозначаются uv
. В
этом случае говорят, что слово v
получается
из слова u
по
правилу .
Правила
грамматики позволяют преобразовать
слова ее полного
словаря.
Для любого g0G
образуется некоторое множество слов
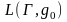 .
.
Определение. Пусть у,z V* – слова над полным словарем V грамматики . Будем говорить, что:
слово z непосредственно выводится из слова у и писать
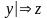 ,если
z
можно получить из у
заменой некоторого его подслова
u
на слово w
по некоторому правилу грамматики
uw,;
,если
z
можно получить из у
заменой некоторого его подслова
u
на слово w
по некоторому правилу грамматики
uw,;
слово z выводится из слова у и писать
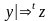 ,если
z
можно получить из слова у
конечным числом замен некоторых подслов
по некоторым
правилам грамматики.
,если
z
можно получить из слова у
конечным числом замен некоторых подслов
по некоторым
правилам грамматики.
Определение. Для произвольно фиксированного грамматического символа g0G множество всех слов над алфавитом А, которые выводятся из g0, обозначается и называется языком, порождаемым грамматикой и начальным символом g0G.
Таким образом, по определению
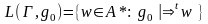 .
.
Примеры.
Пусть грамматика имеет однобуквенный алфавит А = {a}, один грамматический символ g0G, g0 а и два правила: g0а, g0аg0.
Схематически процесс построения языка можно изобразить на следующей диаграмме:
|
|
a
|
|
aa |
|
aaa
|
aaaa |
g0 |
|
ag0 |
|
aag0 |
|
aaag0 |
… |
={a, aa, ааа, aaaa,…}=A+.
2. Пусть грамматика имеет двухбуквенный алфавит А={a,b}, один грамматический символ g0G, g0 а,b и три правила: g0а, g0аba, g0аg0a.
|
a
|
|
aaa
|
|
aaaaa
|
|
|
g0 |
|
ag0a |
|
aag0aa |
|
aaag0aaa |
|
|
aba |
|
aabaa |
|
aaabaaa |
|
|
={a,aba,
а3,
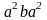 ,a5,
,a5,
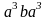 ,…}.
,…}.
В качестве еще одного применения грамматик рассмотрим общепринятый подход к языкам программирования на примере построения известного языка ALGOL 60.
Алфавит А такого языка состоит из букв, цифр, алгебраических символов и специальных зарезервированных слов, его грамматическими символами являются некоторые подмножества множества А* и, наконец, имеются определенные грамматические правила, по которым строятся программы этого языка.
Грамматика с алфавитом
А={А,В,...,Z,а,b,...,z,0,1,…,9,+,,*,/,,,=,,<,,>,,,,,;,,:,(,),[,], BEGIN, TRUE, FALSE, GOTO, FOR, STEP, UNTIL, END}
и множеством грамматических символов G, состоящим из множеств I,U,R,В,D,L,… подмножеств множества A*, которые обозначаются символами <идентификатор>, <целое без знака>, <вещественное>, <булево>, <цифра>, <буква>,… и неявно определяются последовательностью уравнений вида:
I = L IL ID, U = D UD и т.д.,
где IL,ID,UD – произведения подмножеств в полугруппе слов А*.
Эти уравнения определяются соответствующими правилами языка ALGOL:
<идентификатор> ::= <буква> | <идентификатор><буква> | <идентификатор><цифра>,
<число без знака> ::= <цифра>|<число без знака><цифра>, …
Пусть g0 – произвольный начальный символ, удовлетворяющий условию g0A и – множество правил грамматики вида: g0I, g0g0D, g0g07 и т. п. Языки, порождаемые такими грамматиками с произвольным конечным алфавитом А и определяемым уравнениями множеством грамматических символов GА*, называются языками типа ALGOL.
Определение.
Язык LA+
называется
языком, порожденным
грамматикой
(или языком
типа 0), если
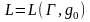 для некоторой грамматики
с начальным символом g0.
для некоторой грамматики
с начальным символом g0.
Теорема 1.
Язык LA+
в том и только
том случае порождается некоторой
грамматикой, если он последовательно
порождается некоторой эффективной
процедурой (алгоритмом) P,
т.е.
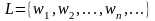 ,
где каждый элемент
,
где каждый элемент
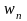 является результатом применения
процедуры P
к последовательным значениям
является результатом применения
процедуры P
к последовательным значениям
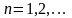 .
.
Такие языки называются рекурсивно перечислимыми.
Определение. Грамматика называется:
контекстно-зависимой (или типа 1), если любое ее правило имеет вид
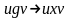 для некоторых
для некоторых
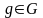 ,
,
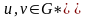 ,
,
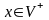 ;
;
контекстно-свободной (или типа 2), если любое ее правило имеет вид
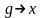 для некоторых
и
;
для некоторых
и
;праволинейной (или рациональной, или типа 3), если любое ее правило имеет вид
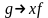 или
или
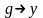 для некоторых
для некоторых
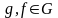 и
и
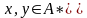 .
.
Для
каждого типа
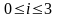 обозначим Ki
класс всех языков, порожденных грамматиками
типа i.
Известно,
что
обозначим Ki
класс всех языков, порожденных грамматиками
типа i.
Известно,
что
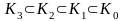 ,
причем все эти включения строгие.
,
причем все эти включения строгие.
Теорема 2. Язык LA+ в том и только том случае порождается некоторой контекстно-зависимой грамматикой, если найдется такая эффективная процедура (алгоритм), которая для любого слова wA+ позволяет определить, принадлежит ли это слово языку L или нет.
Такие языки называются рекурсивными.
Теорема 3. Язык LA+ в том и только том случае порождается некоторой контекстно-свободной грамматикой, если он является языком типа языка программирования ALGOL.
Теорема 4.
Язык LA+
в том и только
том случае порождается некоторой
праволинейной
грамматикой,
если он получается из однобуквенных
языков
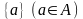 с помощью алгебраических операций
сложение +, умножение
и итерация +.
с помощью алгебраических операций
сложение +, умножение
и итерация +.
Такие языки
называются рациональными,
поскольку они определяются формулами
с постоянными символами
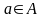 и символами трех алгебраических операций
+,
и +.
Например, рациональный язык в примере
2 определяется формулой
и символами трех алгебраических операций
+,
и +.
Например, рациональный язык в примере
2 определяется формулой
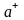 .
.
Так как конструктивные объекты можно кодировать словами конечного множества A (например, состоящего из двоичных символов 0 и 1), то алгоритм моделируется устройством, перерабатывающим слова алфавита A.
Пусть А – произвольное конечное множество, называемое алфавитом.
Элементы aА называются буквами.
Словом
над алфавитом А
называется
конечная последовательность букв
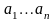 алфавита А.
алфавита А.
Слово без букв
называется пустым
словом и
обозначается символом
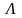 .
.
Обозначим символом
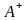 множество всех непустых слов над
алфавитом и символом
множество всех непустых слов над
алфавитом и символом
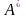 –
множество слов
–
множество слов
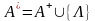 .
.
На этих множествах определена операция умножения слов по следующему правилу:
любым двум словам
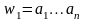 ,
,
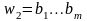 ставится в соответствие слово
ставится в соответствие слово
 ,
,
полученное
в результате приписывания к первому
слову
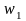 второго слова
второго слова
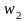 .
.
Подмножества множества называются языками над алфавитом А. Для языков K,L определяются алгебраические операции:
сложение K+L = { u : u K или u L };
умножение
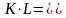 и
и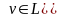 ;
;
итерация
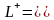 для всех nN}.
Примеры.
для всех nN}.
Примеры.
Для однобуквенного алфавита A={a} словами являются последовательности: a, aa, aaa, …
В этом случае
множества слов
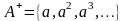 и
и
 являются бесконечными множествами,
которые позволяют кодировать сколь
угодно большие конечные множества B
с помощью
отображений
являются бесконечными множествами,
которые позволяют кодировать сколь
угодно большие конечные множества B
с помощью
отображений
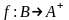 .
.
Языками над алфавитом A={a} являются всевозможные множества слов, образованных из одной буквы a.
2. Для двухэлементного алфавита A={a,b} словами являются последовательности: a, b, aa, ab, ba, bb,…
В этом случае
множество слов
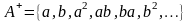 и
и
 также бесконечны.
также бесконечны.
Языками над алфавитом A={a,b} являются всевозможные множества слов, образованных из двух букв a,b.