Метод резолюций в исчислении предикатов

По теореме Эрбрана доказательство противоречивости формул исчисления предикатов сводится к доказательству противоречивости конечных множеств дизъюнктов S.

Обозначим 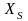, и соответственно множества всех предметных переменных, предметных символов и функциональных символов, встречающихся в формулах множества S. Пусть 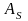– объединение множеств и с добавленным новым постоянным символом a, если .

На множестве определяется множество всех термов 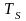множества S с функциональными символами из множества . В частности, каждая переменная 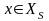является термом из множества и, значит, .

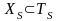Отображения θ множества переменных в множество термов называются подстановками и обозначаются

,

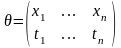где 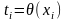для всех 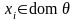, удовлетворяющих ( ).

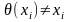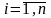При этом подстановка θ называется основной, если все термы не содержат переменных символов.

Действие подстановки θ естественно продолжается на термы из , атомарные формулы, встречающихся в формулах множества S, и дизъюнкты из S.

Например, для терма значение .

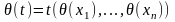Аналогично, для дизъюнкта D значение 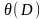– есть дизъюнкт, полученный заменой всех вхождений в D термов t на термы .

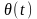Значения и называются примерами соответствующих выражений t и D. При этом примеры называются основными, если подстановка θ основная.

В частности, в силу тождественное преобразование множества является подстановкой, которая обозначается ε и называется пустой.

Очевидно, что такая подстановка оставляет неизменными все термы из и дизъюнкты из S.

Пусть 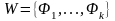– множество атомарных формул, встречающихся в дизъюнктах из множества S. Подстановка θ называется унификатором множества формул W, если

.

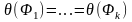Говорят, что множество атомарных формул W унифицируемо, если для него существует унификатор.

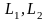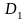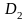Пусть дизъюнкты из множеств S не имеют общих перемен­ных и – литеры в и соответственно.

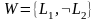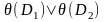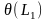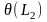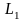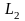Если множество формул имеет унификатор θ, то дизъюнкт, получаемый из дизъ­юнкта вычеркиванием литер и , называется бинарной резольвентой дизъюнктов и , а литеры и называются отрезаемы­ми литерами.

Есл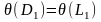и и 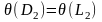, то бинарную резольвенту дизъюнктов и полагаем равной 0.

Резолютив­ный вывод формулы Ф из множества дизъюнктов S есть такая конечная последователь­ность дизъюнктов 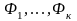, что:

1) ,

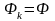2) каждый дизъюнкт 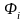или принадлежит множеству S, или является резольвентой дизъюнктов, предшествующих .

Универсальным замыканием формулы 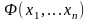называ­ется предложение .

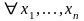Теорема 2 (Tеорема о полноте метода резолюций).

Множество универсальных замыканий формул из множества дизъюнктов S невыполнимо тогда и только тогда, когда существует резолютивный вывод нуля из S. Пример.

Установить, что из посылки "Студенты суть граждане" следует заключение "Голоса студентов суть го­лоса граждан".

Пусть формулы S(x),C(x) и V(x, у) означают:

"х — студент", "х — гражданин" и "x есть голос у" соответственно.

Тогда по­сылка и заключение запишутся следующим образом:

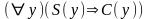(посылка),

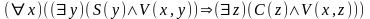(заключение).

Формула, соответствующая посылке, эквивалентна дизъюнкту

.

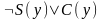С другой стороны, три дизъюнкта

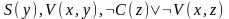
определяют отрицание заключения.

Доказательство противоречивости множества дизъюнктов: