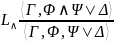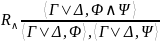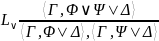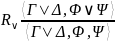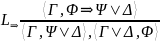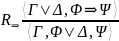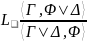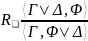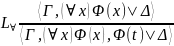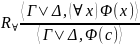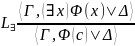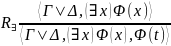- •Логика высказываний.
- •Логическая равносильность формул.
- •Нормальные формы формул алгебры высказываний.
- •Метод резолюций в алгебре высказываний
- •Алгебра логических значений
- •Булевы многочлены и булевы функции
- •Системы булевых функций
- •Переключательные схемы
- •Минимизация булевых многочленов
- •Логика предикатов Понятие предиката
- •Алгебра предикатов
- •Формулы алгебры предикатов
- •Если , – формулы, то формулами являются также выражения
- •Интерпретации формул алгебры предикатов
- •Тавтологии алгебры предикатов
- •Логическая равносильность формул алгебры предикатов
- •Логическое следование формул алгебры предикатов
- •Формальные исчисления
- •Исчисление высказываний
- •Исчисление предикатов
- •Аксиоматические теории первого порядка
- •Интерпретация теории первого порядка
- •Выполнимость формул теории первого порядка
- •Примеры теорий первого порядка
- •Свойства теорий первого порядка
- •Проблема общезначимости формул алгебры предикатов
- •Метод семантических таблиц
- •Автоматическое доказательство теорем
- •Нормальные формы для формул алгебры предикатов
- •Метод резолюций в исчислении предикатов
- •Элементы теории алгоритмов
- •Характерные особенности моделей вычислений Общие понятия алгоритма и вычислимой функции.
- •Формальные грамматики
- •Нормальные алгорифмы Маркова
- •Рекурсивные функции
- •Машины Тьюринга
- •Сложность вычислений
- •Сложность алгоритмов
- •Полиномиальные сведения
Метод семантических таблиц
Рассматривается интерпретация M формул языка УИП сигнатуры .
Семантической
таблицей
называется упорядоченная пара множеств
формул
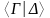 ,
где
– множество истинных для рассматриваемой
интерпретации M
формул и
,
где
– множество истинных для рассматриваемой
интерпретации M
формул и
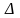 – множество ложных для рассматриваемой
интерпретации M
формул.
– множество ложных для рассматриваемой
интерпретации M
формул.
Семантическая таблица называется выполнимой, если существует такая интерпретация M и такая оценка предметных переменных , что
для любой формулы
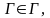
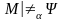 для
любой формулы
для
любой формулы
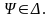
Примеры.
1. Семантическая таблица
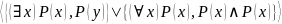
Выполнима
для двухэлементной интерпретации.
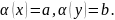
2. Семантическая таблица
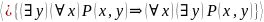
невыполнима.
Теорема (о табличной проверке общезначимости формул).
Для
любой формулы
языка
УИП сигнатуры
условие
выполняется тогда и только тогда, когда
семантическая таблица
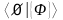 невыполнима.
невыполнима.
Семантическая таблица называется
закрытой, если
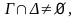
атомарной, если множества
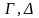 состоят из атомарных формул.
состоят из атомарных формул.
Предложение. Каждая закрытая семантическая таблица невыполнима и каждая незакрытая атомарная семантическая таблица выполнима.
Следствие. Если для формулы языка УИП сигнатуры выполнимость семантической таблицы сводится к выполнимости некоторой закрытой семантической таблицы, то формула общезначима.
Правила корректного преобразования семантических таблиц, сохраняющие выполнимость этих таблиц, называются правилами табличного вывода.
Для
семантических таблиц
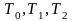 такие правила символически записываются
выражениями вида
такие правила символически записываются
выражениями вида
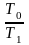 или
или
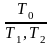 ,
которые означают, что таблица
,
которые означают, что таблица
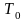 выполнима в том и только том случае,
если выполнима таблица
выполнима в том и только том случае,
если выполнима таблица
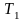 (или, соответственно, одна из таблиц
(или, соответственно, одна из таблиц
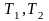 ). Основные
правила табличного вывода
). Основные
правила табличного вывода
|
|
|
|
|
|
|
|
|
|
|
|
где
в правилах
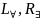 формула (t)
– результат замены всех вхождений
переменной x
в формулу (x)
термом t,
переменные которого не попадают в
формуле
формула (t)
– результат замены всех вхождений
переменной x
в формулу (x)
термом t,
переменные которого не попадают в
формуле
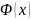 в области действия кванторов по этим
переменным,
в области действия кванторов по этим
переменным,
и
в правилах
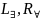 формула (c)
– результат замены всех вхождений
переменной x
в формулу (x)
постоянным символом c,
который
не содержится
ни в формуле
формула (c)
– результат замены всех вхождений
переменной x
в формулу (x)
постоянным символом c,
который
не содержится
ни в формуле
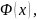 ни в формулах из множеств
ни в формулах из множеств
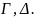
Лемма (корректность основных правил табличного вывода).
Для всех основных правил табличного вывода вида или таблица выполнима в том и только том случае, если выполнима таблица (или, соответственно, одна из таблиц ).
Табличным
выводом
для семантической таблицы
называется корневое дерево, корнем
которого является таблица
и вершинами являются такие семантические
таблицы, что из вершины
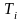 в вершину
в вершину
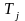 (и в вершину
(и в вершину
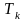 )
идет дуга в том и только том случае, если
)
идет дуга в том и только том случае, если
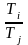 или
или
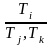 являются правилами табличного вывода.
При этом листьями такого дерева являются
закрытые или атомарные таблицы.
являются правилами табличного вывода.
При этом листьями такого дерева являются
закрытые или атомарные таблицы.
Табличный вывод называется успешным, если он является конечным деревом, все листья которого являются закрытыми таблицами.
Теорема
полноты табличного вывода.
Семантическая таблица
невыполнима в том и только том случае,
если для этой таблицы
 существует успешный табличный вывод.
существует успешный табличный вывод.
Следствие. Формула языка УИП сигнатуры общезначима в том и только том случае, если для семантической таблицы существует успешный табличный вывод.