Свойства теорий первого порядка

Теория первого порядка Th_() называется:

• непротиворечивой, если в ней нельзя доказать никакое предложение  вместе с его отрицанием ;

• полной, если она содержит любое предложение  или его отрицание ;

• разрешимой, если есть эффективная процедура, позволяющая для любой формулы  определить, является она теоремой этой теории или нет.

Теорема Геделя о существовании модели. Теория первого порядка непротиворечива в том и только том случае, если она имеет модель.

В частности, все перечисленные выше теории непротиворечивы.

Теорема Геделя о полноте. Для любого множества формул  языка УИП сигнатуры  теория первого порядка Th_() состоит из тех и только тех формул этого языка, которые общезначимы на всех моделях множества аксиом .

Для алгебраической -системы A обозначим Th_(A) множество всех формул сигнатуры , которые общезначимы на A.

Лемма. Для любой алгебраической -системы A множество формул Th_(A) удовлетворяет следующим свойствам:

1. множество Th_(A) является теорией первого порядка;

2. теория Th_(A) непротиворечивая;

3. теория Th_(A) полная.

В частности, для алгебры неотрицательных целых чисел N₀=(N₀;+,,S,0) множество формул Th_(N₀) языка УИП сигнатуры является полной теорией.

В частности, для алгебры неотрицательных целых чисел N₀=(N₀;+,,S,0) множество формул Th_(N₀) языка УИП сигнатуры является полной теорией.

С другой стороны, теория групп не является полной, так как, например, ни предложение 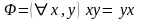, ни его отрицание  не принадлежат этой теории в силу того, что есть как коммутативные, так и некоммутативные группы.

Теорема Геделя о неполноте арифметики. Теория Ar является собственным подмножеством теории Th_(N₀).

Более того, доказано, что теория Th_(N₀) в принципе не имеет разрешимой системы аксиом (для которой есть алгоритм, распознающий по любой формуле языка УИП сигнатуры , является ли она аксиомой или нет).

Проблема общезначимости формул алгебры предикатов

Определение истинности формул языка УИП сигнатуры  вводится с помощью интерпретации этого языка в конкретных алгебраических -системах с первоначально фиксированными предикатными, функциональными и предметными символами сигнатуры . Так как множество таких интерпретаций бесконечно (они могут иметь как конечные, так и бесконечные области интерпретации), то в этом случае проверить тождественную истинность рассматриваемой формулы на всех таких интерпретациях практически невозможно.

Пример. Формула

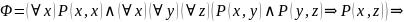
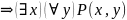
общезначима в любой конечной интерпретации, но не выполнима в интерпретации 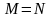с отношением

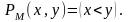
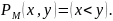
Альтернативный подход к проверке общезначимости формулы  языка УИП сигнатуры  основывается на попытке построения интерпретации, опровергающей данную формулу.

Если из предположения существования такой интерпретации получается противоречие, то формула  общезначима. В противном случае на основе полученных условий для входящих в формулу  предикатов, алгебраических операций и констант строится интерпретация, опровергающая эту формулу , и в этом случае формула  не является общезначимой.

Примеры.

1. Для проверки общезначимости формулы

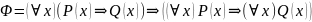
предположим, что эта формула  имеет опровергающую ее интерпретацию M.

2. Для проверки общезначимости формулы

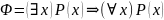
предположим, что эта формула  имеет опровергающую ее интерпретацию M.