
- •Логика высказываний.
- •Логическая равносильность формул.
- •Нормальные формы формул алгебры высказываний.
- •Метод резолюций в алгебре высказываний
- •Алгебра логических значений
- •Булевы многочлены и булевы функции
- •Системы булевых функций
- •Переключательные схемы
- •Минимизация булевых многочленов
- •Логика предикатов Понятие предиката
- •Алгебра предикатов
- •Формулы алгебры предикатов
- •Если , – формулы, то формулами являются также выражения
- •Интерпретации формул алгебры предикатов
- •Тавтологии алгебры предикатов
- •Логическая равносильность формул алгебры предикатов
- •Логическое следование формул алгебры предикатов
- •Формальные исчисления
- •Исчисление высказываний
- •Исчисление предикатов
- •Аксиоматические теории первого порядка
- •Интерпретация теории первого порядка
- •Выполнимость формул теории первого порядка
- •Примеры теорий первого порядка
- •Свойства теорий первого порядка
- •Проблема общезначимости формул алгебры предикатов
- •Метод семантических таблиц
- •Автоматическое доказательство теорем
- •Нормальные формы для формул алгебры предикатов
- •Метод резолюций в исчислении предикатов
- •Элементы теории алгоритмов
- •Характерные особенности моделей вычислений Общие понятия алгоритма и вычислимой функции.
- •Формальные грамматики
- •Нормальные алгорифмы Маркова
- •Рекурсивные функции
- •Машины Тьюринга
- •Сложность вычислений
- •Сложность алгоритмов
- •Полиномиальные сведения
Исчисление предикатов
Множество
аксиом
Ax(ИП)
исчисления
предикатов описывается пятью схемами
аксиом –
тремя определенными в предыдущем разделе
схемами
 ,
в которых
являются
произвольными
формулами исчисления
предикатов, и
двумя новыми схемами:
,
в которых
являются
произвольными
формулами исчисления
предикатов, и
двумя новыми схемами:
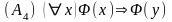
для
произвольной
формулы
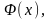 в которую y
не входит
связно;
в которую y
не входит
связно;
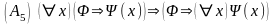
для таких формул , что x в формулу не входит свободно.
Исчисление предикатов имеет два правила вывода – правило modus ponens (сокращенно, MP) и правило обобщения (сокращенно, Gen), которые для произвольных формул исчисления предикатов символически записываются следующими схемами:
и
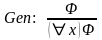 .
.
Определение.
Формула
называется теоремой
исчисления предикатов,
если найдется такая последовательность
,
в которой
=
и каждая
формула
либо является аксиомой, либо
получается из некоторых предыдущих
формул этой последовательности
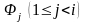 по
одному из правил вывода MP
или
Gen.
При
этом
называется выводом
или
доказательством
формулы
.
по
одному из правил вывода MP
или
Gen.
При
этом
называется выводом
или
доказательством
формулы
.
Вывод формулы обозначают | и говорят, что « есть теорема». Множество всех таких теорем обозначается символом Th(ИП) и называется теорией исчисления предикатов.
Цель построения исчисления предикатов - определение такой теории Th(ИП), которая совпадает с множеством тавтологий TАП.
Лемма 1.
Справедливы следующие утверждения:
всякая аксиома ИП является тавтологией;
результат применения правил вывода MP и Gen к тавтологиям является тавтологией;
любая теорема ИП является тавтологией АП, т.е. имеет место включение Th(ИП)TАП.
Доказательство TАПTh(ИП) было получено австрийским математиком К.Геделем в 1930 году.
Теорема полноты ИП.
Формула исчисления предикатов в том и только том случае является тавтологией, если она есть теорема ИП, т.е. выполняется равенство TАП=Th(ИП).
Таким образом, ИП является адекватным инструментом получения логических законов.
Теорема о непротиворечивости ИП.
В исчислении предикатов невозможно доказать никакую формулу вместе с ее отрицанием .
С другой стороны, английский математик А.Черч в 1936 году доказал следующий принципиально важный результат.
Теорема о неразрешимость ИП.
Не существует универсальной эффективной процедуры (алгоритма), которая для любой формулы определяет, является ли эта формула теоремой ИП.
Таким образом, исчисление предикатов в отличие от исчисления высказываний является не только адекватным, но и безальтернативным инструментом получения логических законов.
Аксиоматические теории первого порядка
При
исследовании конкретной математической
теории фиксируют некоторые наборы
исходных предикатных символов
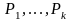 соответствующей арности
соответствующей арности
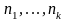 ,
исходных функциональных символов
,
исходных функциональных символов
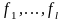 соответствующей арности
соответствующей арности
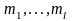 и исходных предметных символов
и исходных предметных символов
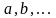 .
.
Множество
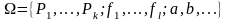 называется алгебраическим
типом
или сигнатурой
математической теории.
называется алгебраическим
типом
или сигнатурой
математической теории.
Принципиальное отличие УИП от ИП заключается в следующем.
1. Алфавит УИП состоит из предметных переменных, логических и вспомогательных символов, а также некоторых исходных предикатных символов соответствующей арности , некоторых исходных функциональных символов соответствующей арности и некоторых исходных предметных символов .
В результате элементы области интерпретации такого языка будут описываться не только с помощью предметных переменных, но и с помощью так называемых термов – специальных выражений языка, которые индуктивно определяются следующим образом:
а) все предметные переменные и предметные символы являются термами,
б)
если f
–
сигнатурный n-арный
функциональный символ и
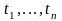 – термы, то выражение
– термы, то выражение
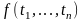 является термом.
является термом.
2.
Формулы
УИП определяются
по аналогии с формулами ИП за исключением
исходного шага индукции – определения
атомарных формул, которые в данном
случае имеют вид выражений
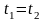 ,
,
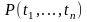 для любых термов
для любых термов
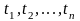 и сигнатурных n-арных
предикатных символов
P.
и сигнатурных n-арных
предикатных символов
P.
Записывают , если в формулу входят предметные переменные .
Формула без свободных вхождений переменных называется замкнутой формулой или предложением.
3.
Множество аксиом
УИП
описывается пятью определенными в
предыдущем разделе схемами
аксиом
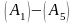 ,
в которых
теперь являются
произвольными
формулами УИП,
и дополнительной системой формул
специальных аксиом рассматриваемой
математической теории. Аксиомы первого
вида называются логическими
и аксиомы второго вида – нелогическими
аксиомами УИП.
,
в которых
теперь являются
произвольными
формулами УИП,
и дополнительной системой формул
специальных аксиом рассматриваемой
математической теории. Аксиомы первого
вида называются логическими
и аксиомы второго вида – нелогическими
аксиомами УИП.
4. Правилами вывода УИП являются правило modus ponens (MP) и правило обобщения (Gen).
5. Формула называется теоремой УИП, если найдется такая конечная последовательность формул , в которой = и каждая формула либо является логической аксиомой из схем , либо является нелогической аксиомой из множества , либо получается из некоторых предыдущих формул этой последовательности по одному из правил вывода MP или Gen.
Последовательность формул называется выводом или доказательством формулы .
Вывод формулы сокращенно обозначают символом | и говорят, что « есть теорема». Множество всех таких теорем обозначается символом Th() и называется элементарной теорией (или теорией первого порядка) узкого исчисления предикатов сигнатуры с множеством аксиом .
Принципиальное отличие интерпретации формул языка УИП от описанной ранее интерпретации формул алгебры предикатов заключается в том, что определение истинности формул УИП сигнатуры вводится с помощью интерпретации этого языка в конкретных алгебраических системах с первоначально фиксированными предикатными, функциональными и предметными символами сигнатуры .
Для придания
содержательного смысла формулам УИП
сигнатуры
сначала
задается область
интерпретации
– непустое множество M,
которое является областью возможных
значений всех предметных переменных,
и затем на
этом множестве
M
для
каждого символа сигнатуры
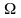 фиксируется соответствующий математический
объект: для
каждого предикатного
символа
фиксируется соответствующий математический
объект: для
каждого предикатного
символа
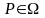 арности
арности
 фиксируется
-арное
отношение
фиксируется
-арное
отношение
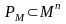 на множестве
M,
для
каждого функционального
символа
на множестве
M,
для
каждого функционального
символа
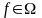 арности
фиксируется
-арная
алгебраическая операция
арности
фиксируется
-арная
алгебраическая операция
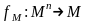 на множестве
M
и для
каждого предметного
символа
на множестве
M
и для
каждого предметного
символа
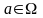 фиксируется элемент
фиксируется элемент
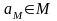 в множестве
M.
в множестве
M.
В
результате получается алгебраическая
система с основным множеством M,
которая называется алгебраической
-системой
и обозначается
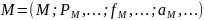 или просто
или просто
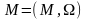 .
Такая система
называется также
интерпретацией
языка УИП
сигнатуры
.
.
Такая система
называется также
интерпретацией
языка УИП
сигнатуры
.
Конкретные значения предметным переменным по-прежнему присваиваются с помощью оценок предметных переменных, т.е. отображений таких переменных в область интерпретации M.
