
- •Логика высказываний.
- •Логическая равносильность формул.
- •Нормальные формы формул алгебры высказываний.
- •Метод резолюций в алгебре высказываний
- •Алгебра логических значений
- •Булевы многочлены и булевы функции
- •Системы булевых функций
- •Переключательные схемы
- •Минимизация булевых многочленов
- •Логика предикатов Понятие предиката
- •Алгебра предикатов
- •Формулы алгебры предикатов
- •Если , – формулы, то формулами являются также выражения
- •Интерпретации формул алгебры предикатов
- •Тавтологии алгебры предикатов
- •Логическая равносильность формул алгебры предикатов
- •Логическое следование формул алгебры предикатов
- •Формальные исчисления
- •Исчисление высказываний
- •Исчисление предикатов
- •Аксиоматические теории первого порядка
- •Интерпретация теории первого порядка
- •Выполнимость формул теории первого порядка
- •Примеры теорий первого порядка
- •Свойства теорий первого порядка
- •Проблема общезначимости формул алгебры предикатов
- •Метод семантических таблиц
- •Автоматическое доказательство теорем
- •Нормальные формы для формул алгебры предикатов
- •Метод резолюций в исчислении предикатов
- •Элементы теории алгоритмов
- •Характерные особенности моделей вычислений Общие понятия алгоритма и вычислимой функции.
- •Формальные грамматики
- •Нормальные алгорифмы Маркова
- •Рекурсивные функции
- •Машины Тьюринга
- •Сложность вычислений
- •Сложность алгоритмов
- •Полиномиальные сведения
Логика высказываний.
Высказывание - повествовательное предложение, о котором можно судить, истинное оно или ложное.
Обозначаются высказывания A,B,C,…
Истинностное значение высказывания A обозначается символом (A) и определяется по формуле:
(A)=1, если высказывание A истинно, и
(A)=0, если A ложно.
Определение.
Алгеброй
высказываний
называется множество всех высказываний
P
с логическими
операциями
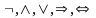 .
.
Свойства алгебры высказываний P описываются с помощью формул, которые строятся из переменных символов с помощью знаков логических операций. Такие формулы приято называть также пропозициональными формулами
Cимволы логических операций , которые называются пропозициональными связками.
Переменные символы X,Y,Z,…, которые используются для обозначения высказываний и которые называются пропозициональными переменными.
Определение. Формулы алгебры высказываний индуктивно определяются по правилам:
каждая пропозициональная переменная является формулой,
если , – формулы, то формулами являются также выражения
(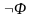 ),
),
 ,
,
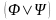 ,
,
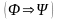 ,
,
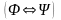 .
.
Множество всех формул алгебры высказываний обозначим FАВ .
Если в формулу
входят переменные
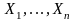 ,
то записывают
,
то записывают
 .
.
Из индуктивного
определения формул следует, что если в
формулу
вместо переменных
подставить произвольные конкретные
высказывания
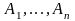 ,
то получится некоторое сложное
высказывание
,
то получится некоторое сложное
высказывание
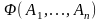 .
.
Истинностное
значение высказывания
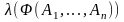 определяется истинностными значениями
исходных высказываний
определяется истинностными значениями
исходных высказываний
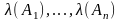 согласно таблицам истинностных значений
логических операций
.
согласно таблицам истинностных значений
логических операций
.
Определение.
Формула
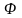 называется:
называется:
тавтологией (или тождественно истинной формулой) и обозначается
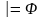 ,
если ее истинностная функция тождественно
равна 1;
,
если ее истинностная функция тождественно
равна 1;
противоречием (или тождественно ложной формулой), если ее истинностная функция тождественно равна 0;
выполнимой, если ее истинностная функция не равна тождественно 0;
опровержимой, если ее истинностная функция не равна тождественно 1.
Тавтологии являются общими схемами построения истинных высказываний и в этом смысле выражают некоторые логические законы.
Примеры таких законов являются:
 –
закон
исключенного третьего,
–
закон
исключенного третьего,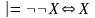 –
закон
двойного отрицания,
–
закон
двойного отрицания,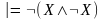 –
закон
противоречия,
–
закон
противоречия,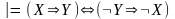 –
закон
контрапозиции.
–
закон
контрапозиции.
Новые тавтологии можно получить с помощью следующих правил.
-Правило отделения:
если
,
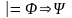 ,
то
,
то
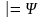 .
.
Правило подстановки:
если
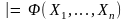 ,
то для любых формул
,
то для любых формул
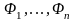 тавтологией является формула
тавтологией является формула
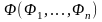 .
.
Логическая равносильность формул.
Определение.
Формулы
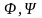 называются логически
эквивалентными (или
просто равносильными),
если
называются логически
эквивалентными (или
просто равносильными),
если
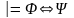 .
.
Для
обозначения логически эквивалентных
формул используется символическая
запись
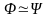 ,
или просто
,
или просто
 .
.
Такие выражения называются логическими эквивалентностями или просто равенствами формул.
Лемма. Справедливы следующие равенства формул:
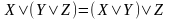 ,
,
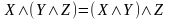 – свойства ассоциативности дизъюнкции
и конъюнкции;
– свойства ассоциативности дизъюнкции
и конъюнкции;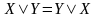 ,
,
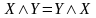 – свойства коммутативности дизъюнкции
и конъюнкции;
– свойства коммутативности дизъюнкции
и конъюнкции;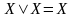 ,
,
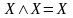 – свойства идемпотентности дизъюнкции
и конъюнкции;
– свойства идемпотентности дизъюнкции
и конъюнкции; ,
,
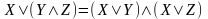 – законы дистрибутивности конъюнкции
относительно дизъюнкции и дизъюнкции
относительно конъюнкции;
– законы дистрибутивности конъюнкции
относительно дизъюнкции и дизъюнкции
относительно конъюнкции;
5)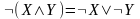 ,
,
 – законы де Моргана;
– законы де Моргана;
6)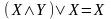 ,
,
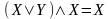 – законы поглощения;
– законы поглощения;
7)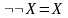 – закон
двойного отрицания;
– закон
двойного отрицания;
8)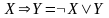 ,
,
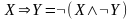 – взаимосвязь импликации с дизъюнкцией
и конъюнкцией;
– взаимосвязь импликации с дизъюнкцией
и конъюнкцией;
9)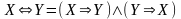 ,
,
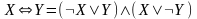 – взаимосвязь эквивалентности с
импликацией, дизъюнкцией и конъюнкцией.
– взаимосвязь эквивалентности с
импликацией, дизъюнкцией и конъюнкцией.
Лемма (Правило
замены). Если
формулы
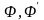 равносильны, то для любой формулы
равносильны, то для любой формулы
 ,
содержащей
переменную X,
выполняется
равенство:
,
содержащей
переменную X,
выполняется
равенство:
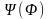 =
=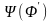 .
.
Это правило
означает, что при замене в любой формуле
 некоторой ее подформулы
на равносильную ей формулу
некоторой ее подформулы
на равносильную ей формулу
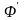 получается формула
получается формула
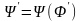 ,
равносильная исходной формуле
,
равносильная исходной формуле
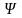 .
.
Такие переходы называются равносильными преобразованиями формул.
